Rike hat sich nach dem Abendessen mit dem Newton-Verfahren und seiner Implementierung auf einem wissenschaftlichen Taschenrechner beschäftigt. Sie hat das allerbeste Skipisten-Beispiel überprüft und andere Beispiele untersucht. Schließlich ist sie dann sehr spät nachts zu Charly ins Bett gekrochen. Dann hat sie (wieder einmal) schlecht geträumt. Beim Frühstück erzählt sie Charly ihren Traum. Weiterlesen

Die Entfernung der allerbesten Skipiste zum Mittelpunkt der Erde
Rike hat in Erwartung der Berechnung einer Skipiste in einer abwechslungsreichen Landschaft mit starken Abfahrten ins Ungewisse die ganze Nacht vom Skifahren geträumt. Sie ist immer wieder ins "schwarze Loch" gefahren und mehrfach hochgeschreckt. (Charly hatte ihr zwar das File mit der Aufgabe nicht gegeben, aber sie dann doch irgendwie beruhigt.) Ob sie wohl die Länge der Strecke ins "schwarze Loch" ausrechnen soll? Oder die Geschwindigkeit eines Skifahrers oder den Abstand von zweien?
Charly Nein, Rike, diese Abfahrt für große x und negative a brauchst du nicht zu fahren! Die Strecke auf dem Höhenzug fmax, den du ausgerechnet hast, ist doch viel schöner: freier Blick nach vorn, rechts und nach links, das ist die allerbeste Piste!
Rike Okay, fmax ist die allerbeste Piste! Charly, nun sag schon, was ist die nächste Teilaufgabe? Ich hätte tausend verrückte Vorschläge!

Die Trainingsstrecken-Aufgabe
Charly sitzt an diesem verregneten und windigen Osterferientag an einer „sportlichen“ Abiaufgabe. Es ist eine typische Analysis-Aufgabe über eine Funktionenschar mit einem Parameter. In dieser Aufgabe werden Nullstellenberechnung, Flächenberechnung, Kurvendiskussion, topologische Eigenschaften, numerische Näherungsverfahren, Zahlentheorie und nicht zuletzt eine Anwendung kombiniert. Die Aufgabe, die einen wissenschaftlichen Taschenrechner als Hilfsmittel zulässt, hat 13 Teilaufgaben. Man kann insgesamt für die Aufgabe 50 Punkte erhalten. Da kommt Rike dazu.
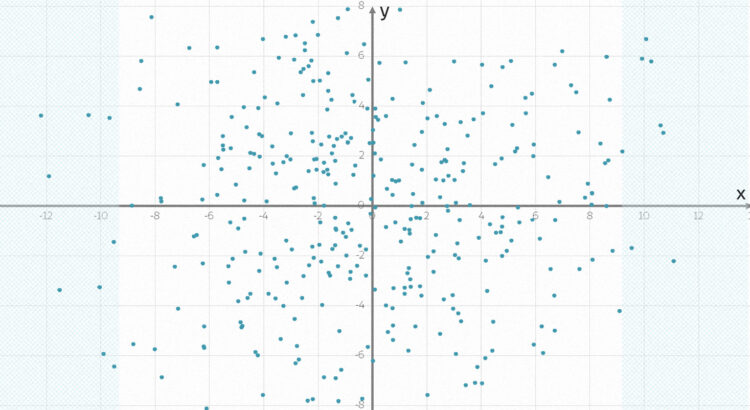
Was sind gute Zufallszahlen?
Charly und Rike feiern heute ihre neue Wohnung. Ein paar Freunde sind gekommen, so auch Ida. Ida macht gerade ihr Refendariat in Informatik an einem Gymnasium. Sie hat ein kleines Problem zur Berechnung von Zufallszahlen mitgebracht, das sie mit Rike besprechen möchte.
Rike Ida, na, wie geht es dir an deiner Schule?
Ida So weit so gut. In Informatik habe ich eine tolle 10. Klasse, wir haben Python zusammen kennengelernt. Das hat Spaß gemacht!
Rike Das hört sich gut an.
Ida Bei meiner Vorbereitung bin ich aber auf ein Problem gestoßen, das ich alleine nicht lösen kann. Vielleicht kannst Du mir helfen?
Rike Ich versuch’s! Erzähl‘ doch mal!
Ein 16x16-Gleichungssystem für die Spline-Aufgabe
– Fortsetzung der Lösung der Spline-Aufgabe –
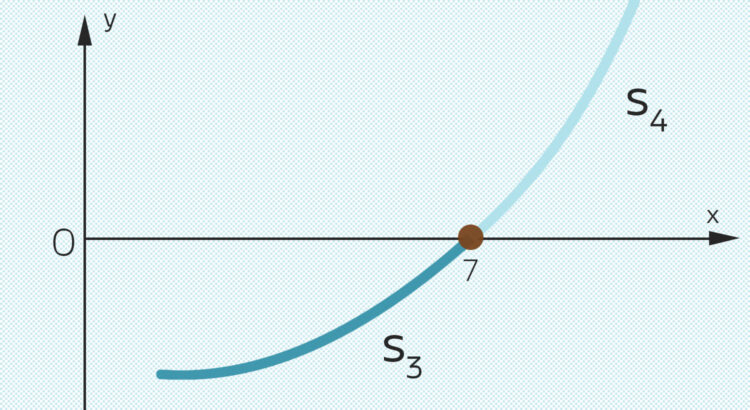
Rike Schade, dass der Ansatz für größere  nicht aufgeht. Doch wenn dir die Nullstelle bei
nicht aufgeht. Doch wenn dir die Nullstelle bei 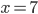 so wichtig ist, dann machen wir eben einen neuen Ansatz und fordern, dass das Spline genau diese Nullstelle oder besser ausgedrückt: genau diese Stützstelle hat.
so wichtig ist, dann machen wir eben einen neuen Ansatz und fordern, dass das Spline genau diese Nullstelle oder besser ausgedrückt: genau diese Stützstelle hat.
Spline-Ansatz mit 4 Stücken
Charly Ja, das ist mir wichtig. Sehe ich das richtig, dass wir bei 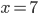 noch einmal stückeln?
noch einmal stückeln?
Rike Ja.
Charly Warte, dann haben wir 4 Polynome.
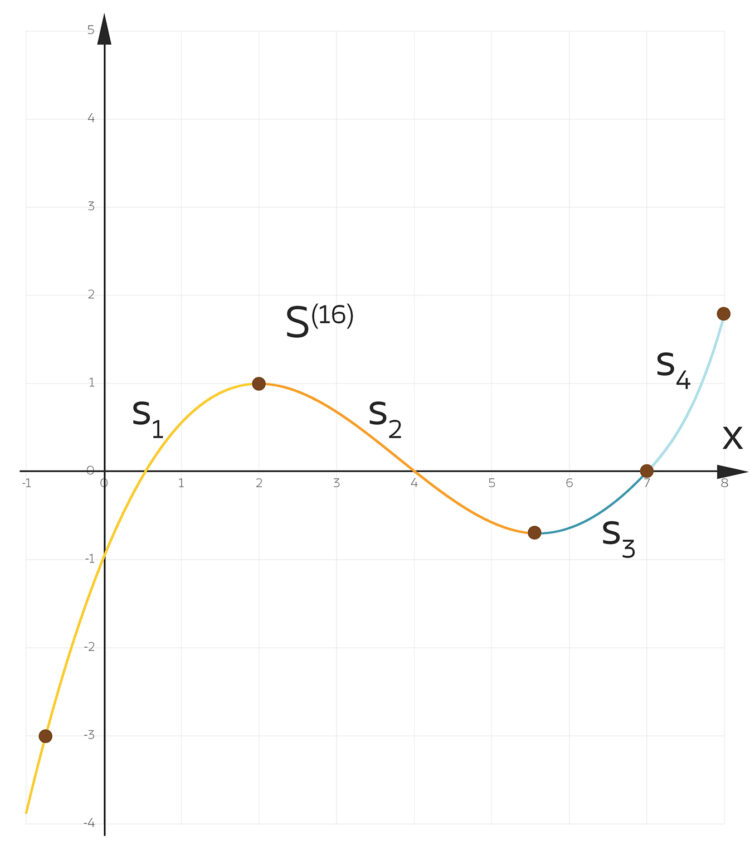
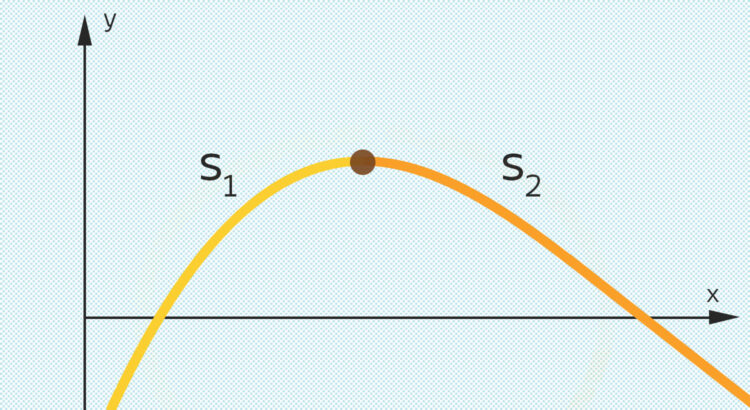
Wie aus der schrägen Ellipsenaufgabe eine Spline-Aufgabe wird
Als Charly vom Joggen wiederkommt, findet er Rike ganz verzweifelt. Sie hat sich die schräge Ellipsenaufgabe noch einmal vorgenommen und Charlys Funktion 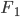
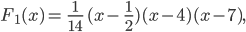
genauer angeschaut. Sie bemerkt, dass diese Funktion 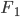 nur für einige
nur für einige  sehr gut mit der Vorlage übereinstimmt, aber leider nicht an anderen wichtigen Punkten.
sehr gut mit der Vorlage übereinstimmt, aber leider nicht an anderen wichtigen Punkten.

Die schräge Ellipsenaufgabe
Als Rike vom Joggen wiederkommt, findet sie Charly ganz verzweifelt. Der Stundenplan fürs neue Schuljahr steht so gut wie fest und wie es aussieht, soll Charly neben Sport wieder einen Abikurs in Mathe übernehmen. So hat er sich weitere Abiaufgaben von Berlin-Brandenburg angeschaut, so auch die (hilfsmittelfreie) Analysis-Aufgabe für den Leistungskurs von 2021. In dieser Aufgabe geht es darum, aus einer Grafik für eine Stammfunktion 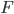 die zugehörige Funktion
die zugehörige Funktion
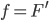
zu finden und deren Eigenschaften zu diskutieren.
Die grafische Darstellung der Funktion F
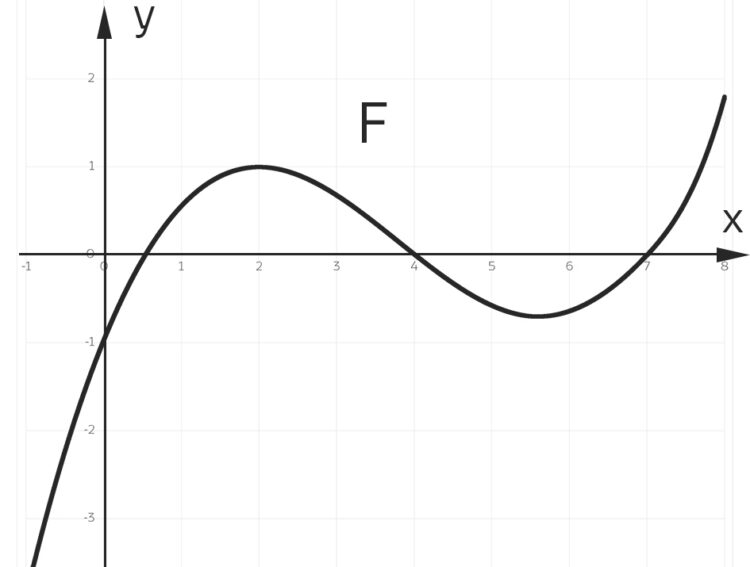
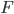 . Abbildung nach [Ott, Schomburg, 2021]
. Abbildung nach [Ott, Schomburg, 2021]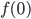 von
von  an der Stelle
an der Stelle 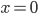 „näherungsweise“ bestimmt werden. Er zeigt Rike die Aufgabe.
„näherungsweise“ bestimmt werden. Er zeigt Rike die Aufgabe.
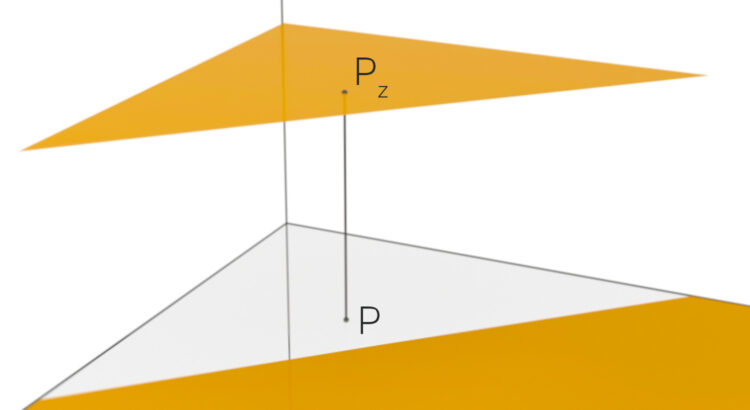
KI-Variationen einer Klausuraufgabe
Rike kommt für einen kurzen Besuch an ihre ehemalige Uni, wo sie früher Mathetutorien gegeben hat. Sie lässt sich die neusten Matheklausuren zeigen. Die von der 3D-Darstellung von Funktionen zweier Veränderlicher hat es ihr besonders angetan. Wie schön die ist, seufzt sie.

Charlys Lösung der IGA-Aufgabe
Charly wundert sich, dass Rikes "seriöse" Lösung der IGA-Abiaufgabe ein anderes Ergebnis als die Musterlösung liefert. Rike hat ein regelmäßiges Muster, das die Anforderung von 6 Blumen pro m² erfüllt, gefunden und damit die gegebene Fläche  zwischen den Kurven
zwischen den Kurven 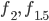 und der
und der  -Achse von knapp 30 m² ausgelegt.
-Achse von knapp 30 m² ausgelegt.
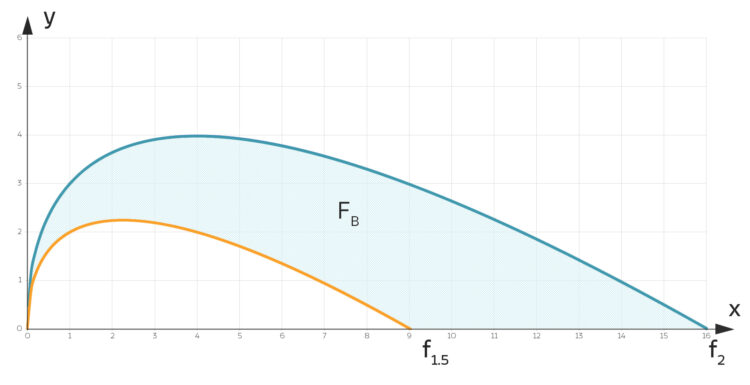
 , die mit Blumen zu belegen ist. Für die Formeln von
, die mit Blumen zu belegen ist. Für die Formeln von 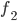 und
und 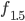 siehe Beitrag Die IGA-Aufgabe.
siehe Beitrag Die IGA-Aufgabe.Bei der Musterlösung war die Fläche unabhängig von der Geometrie zu bepflanzen – aber eben nur im Mittel.

Rikes seriöse Lösung der IGA-Aufgabe
Rike hat schon gemerkt, dass ihre zufällige Anordnung von 6 Blumen pro Quadratmeter Charly in der IGA-Aufgabe nicht gefallen hat, ja, dass diese Lösung nicht nur Charly nicht gefällt sondern auch auf der IGA 2017 keinen Beifall gefunden hätte. So überlegt sie, ob es nicht doch eine seriöse Lösung gibt. Sie erinnert sich, dass Gärtner häufig diagonale Anordnungen benutzen. Eine Diagonale ergäbe so ein 5er Muster. Weiterlesen