Trainingsstrecken-Aufgaben
Aufgabe und Lösung stammen aus:
Mathematik Abitur 2024. Leistungskurs. Berlin und Brandenburg. Prüfungen und Lösungen, L&K development GmbH, Berlin, 2023, S. 43 ff., S. 112 ff.
Mathematical Image Analysis Group: Das Newton-Verfahren, mia.uni-saarland.de, Universität des Saarlandes, letzter Aufruf am 05.04.2024.
Bigalke, Anton; Köhler, Norbert (Hrsgb.): Mathematik. Band 1. Analysis, Cornelsen Verlag, Berlin, 2013, S. 124 ff. Das Zitat stammt von S. 125. Das Beispiel zur Quadratwurzel ist auf S. 128.
fx-570EX, FX-991EX User's Guide, CASIO COMPUTER CO., LTD., Tokio/Norderstedt, 2015, S. 19. casio-manual.pdf, letzter Aufruf am 18.04.2024
Das Titelbild wurde von Stability AI erzeugt, Prompt: “A boy and girl with ski running in a great landscape..., digital art”, 02.04.2024, und danach von M.E. bearbeitet
Das Titelbild für Teil 2: Die Entfernung der besten Skipiste zum Mittelpunkt der Erde wurde ebenfalls von Stability AI erzeugt, Prompt: “a fantasy winter landscape with ski trail in white, blue and little orange colors..., digital art”, 03.04.2024, und danach von M.E. bearbeitet
Das Titelbild für Teil 3: Rikes Begegnung mit Newton wurde ebenfalls von Stability AI erzeugt, Prompt: “a young man with long gray hair, beardless in front of a fantasy winter landscape with big mountains in a lot of white, blue and some orange colors,” und Vorlage des Newton-Porträts von Godfrey Kneller, 10.04.2024, und danach von M.E. bearbeitet
Splines
de.wikipedia.org/wiki/Spline-Interpolation, Aufruf am 26.05.202.
en.wikipedia.org/wiki/Spline_interpolation, Aufruf am 26.05.202.
Für Anwendungen in der Computergrafik siehe:
Eric Lengyel: Mathematics for 3D Game Programming and Computer Graphics, 3. Aufl., Course Technology, 2012, S. 317-359.
Die schräge Ellipsenaufgabe
Roland Ott, Wolfgang Schomburg: Abitur 2022. Aufgabensammlung zur zentralen schriftlichen Abiturprüfung Berlin/Brandenburg Mathematik, Merkur Verlag Rinteln, 4. Aufl. 2021, S. 203.
Bob Blume: Tötet ChatGPT das Lernen? https://bobblume.de/2022/12/14/toetet-chatgpt-das-lernen/, Aufruf am 15.05.202.
AI-generierte Bilder
Aditya Ramesh, Prafulla Dhariwal, Alex Nichol, Casey Chu, Mark Chen: Hierarchical Text-Conditional Image Generation with CLIP Latents, https://arxiv.org/abs/2204.06125, Aufruf am 26.10.2022.
Chitwan Saharia, William Chan, Huiwen Chang, Chris A. Lee, Jonathan Ho, Tim Salimans, David J. Fleet, Mohammad Norouzi: Palette: Image-to-Image Diffusion Models, ACM SIGGRAPH, August 8-11, 2022, Vancouver, https://arxiv.org/abs/2111.05826, Aufruf am 26.10.2022.
Dr. Mike Pound: How AI Image Generators Work (Stable Diffusion / Dall-E) - Computerphile, https://www.youtube.com/watch?v=1CIpzeNxIhU, Aufruf am 26.10.2022.
Jonathan Ho; Ajay Jain, Pieter Abbeel: Denoising Diffusion Probabilistic Models, 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada, https://arxiv.org/pdf/2006.11239.pdf, 07.12.2022.
Wiki Diffusion model: wiki/Diffusion_model, 07.12.2022
Ari Seff: What are Diffusion Models?
vom 20.04.2022, www.youtube.com
Die rot-grüne Urnenaufgabe
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, Analysis-Aufgabe von 2019, S. 38 f., S. 48 f., https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Rikes alternative Bonsai-Aufgabe
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, Analysis-Aufgabe von 2019, S. 72 f. https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Bonsais
https://bonsai.org/de/
https://www.bonsaiempire.de/grundlagen
https://www.bonsai-shop.com/bonsai/kiefern,
Aufrufe am 05.08.2022.
Die Gutschein-App
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, Stochastik-Aufgabe von 2021, S. 13, 35 f. https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Die rot-grüne Programmieraufgabe
Das Gesetz der großen Zahlen - Satz von Bernoulli, Version aus
B. W. Gnedenko: Lehrbuch der Wahrscheinlichkeitsrechnung, Berlin, 1979, S. 189.
Die rot-grüne Würfelaufgabe
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, S. 44, 64 f. https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Zum Wahrscheinlichkeitsbegriff und -auffassungen
Stuart J. Russell; Peter Norvig: Artificial Intelligence. A Modern Approach, Pearson, 3. Aufl., 2016, S. 490 f.
Absurde Bevölkerungsstruktur und Freizeitverhalten
Studien zur Freizeit (leider nicht vom Autor verwendet)
https://de.statista.com/themen/64/freizeit/#topicHeader__wrapper
http://www.freizeitmonitor.de/
Abiaufgabe 2017 vom Bildungsserver Berlin-Brandenburg: https://bildungsserver.berlin-brandenburg.de/fileadmin/bbb/unterricht/pruefungen/abitur_bb/Zabi_Mathematik/17_Ma_LK_CAS_Aufgaben_neu.pdf, S. 9
Benutze Zahnarztstudie
Nele Kettler, Regine Chenot und A. Rainer Jordan: Subjektives Qualitätsverständnis von Vertragszahnärzten im Umgang mit Qualitätsmanagement- Ergebnisse eines bundesweiten Surveys von Health insurance dentists’ subjective perceptions of quality when implementing quality management in practice – results from a nationwide survey - Zeitschrift für Evidenz, Fortbildung und Qualität im Gesundheitswesen (zefq-journal.com), 2015, S. 695-703.
Yuri I. Manin, Matilde Marcolli: Semantic Spaces, 2016, Math. Comput. Sci. 10, no. 4, 2016, S. 459-477, https://arxiv.org/pdf/1605.04238.pdf
Aufruf am 18.5.2022 für alle
Sigma-Regeln und Zahnarztaufgabe
Zahnärztliche Studien
Vom Institut der Deutschen Zahnärzte:
Kassenzahnärztliche Bundesvereinigung, Geschäftsbericht 2013/2014:
https://www.kzbv.de/geschaeftsbericht-2013-2014.877.de.html
Aufruf am 1.5.2022 für alle
Potsdam, Sportschule, Bevölkerung
https://de.wikipedia.org/wiki/Sportschule_Potsdam_%E2%80%9EFriedrich_Ludwig_Jahn%E2%80%9C
https://de.wikipedia.org/wiki/Potsdam
Aufruf am 1.5.2022 für alle
Statistikaufgaben und -thoerie
bildungsserver.berlin-brandenburg, 2015, S. 9, letzter Aufruf am 08.05.2022
Norbert Henze: Stochastik für Einsteiger. Eine Einführung in die faszinierende Welt des Zufalls. 10. Aufl., Springer-Spektrum, 2013, S. 221 ff.
Anton Bigalke, Norbert Köhler (Hrsg.): Mathematik, Gymnasiale Oberstufe, Grundkurs, 12. Cornelsen, 2020, S. 210 ff.
Modell des Gebisses
von VikingDigital auf Turbosqiud.com, Aufruf am 07.05.2022
Satz von Moivre-Laplace
B. W. Gnedenko: Lehrbuch der Wahrscheinlichkeitsrechnung. Akademie-Verlag Berlin, 1979, S. 80 ff.
Wissenschaftlicher Taschenrechner von Casio
https://www.casio-schulrechner.de/de/produkte/software/classwizemulator/
https://support.casio.com/storage/de/manual/pdf/DE/004/fx-87_991DEX_DE.pdf
Aufruf am 21.04.2022 für beide
en.wikipedia.org/wiki/De_Moivre , Aufruf am 13.04.2022.
Flaubert und Python
Für das Titelbild wurde das folgende Bild von Flaubert auf Wikipedia verwendet:
https://fr.wikipedia.org/wiki/Gustave_Flaubert#/media/Fichier:Gustave-Flaubert2.jpg, Aufruf am 22.03.2022.
Mathematische Erektionen
Gustave Flaubert: Briefe. Herausgegeben und übersetzt von Helmut Scheffel, Diogenes, 1977.
Wörterbuch der Gepflogenheiten: S. 153, 223
Brief an Louise Colet: S. 224 ff.
Frz. Originaltext: S. 752
Charakter im Titelbild: Whiteclown N Hallin von Deadgnv auf mixamo.com, Pose auch von mixamo.com Aufruf am 08.03.2022.
Paulas merkwürdige Sägezahnkurve
Rike hat den RSA-Algorithmus für Max in einem 15. Beitrag unseres Blogs von 2015-2017 und einem vollständig berechneten Beispiel mit kleinem 
dargelegt, das findet sich jetzt in einem E-Book Mathezartbitter. Die Effi-Briest-Analyse ist dort ebenfalls, Beiträge 54-59.
Die neue Sichtweise auf den RSA-Algorithmus und das Beispiel mit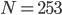 
gehen auf das folgende Buch zurück:
Johannes Buchmann: Einführung in die Krytographie, Springer, 4. Aufl., 2008
Düsseldorfer Kaffee-Aufgabe und die Methode der kleinsten Quadrate
Die Aufgabe
Standardsicherung NRW, S. 3 ff. Aufruf am 17.08.2021.
Methode der kleinsten Quadrate
https://de.wikipedia.org/wiki/Methode_der_kleinsten_Quadrate, Aufruf am 17.08.2021.
PDEs und Maschinelles Lernen
Zongyi Li et al.: Fourier Neural Operator For Parametric Partial Differential Equations, Version vom 17.05.2021, https://arxiv.org/pdf/2010.08895.pdf, Version vom 17.05.2021, Letzter Aufruf: 23.06.2021.
Anil Ananthaswamy: Latest Neural Nets Solve World’s Hardest Equations Faster Than Ever Before, Quantamagazine, Version vom 19.4.2021, https://www.quantamagazine.org/new-neural-networks-solve-hardest-equations-faster-than-ever-20210419/, Letzter Aufruf: 23.06.2021.
Jon McLoone: From Zero to AI in 60 minutes: https://www.wolfram.com/wolfram-u/machine-learning-zero-to-AI-60-minutes/ Letzter Aufruf am 20.06.2021.
Die rückwärtige Wärmeleitungsgleichung
K. Eriksson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul. Bd. 3, 2003, Heidelberg, S. 1140-1143.
A. A. Samarskij: Theorie der Differenzenverfahren, Leipzig, 1984, S. 32, 169-179.
John Archibald Wheeler: Frontiers of Time, Vortrag auf der International School of Physics Enrico Fermi, Varenna, 1977, S. 46, 134.
Integraltrichter
Peter Deufhard, Folkmar Bornemann: Numerische Mathematik 2. Gewöhnliche Differentialgleichungen, 3. Aufl., 2008, Berlin, S. 51-56.
Hellmuth Kneser: Über die Lösung eines Systems gewöhnlicher Differentialgleichungen, das der Lipschitzchen Bedingung nicht genügt, S.-B. Preuß. Akad. Wiss. Phys. Math. KI. (1923), 171-174.
Charles C. Pugh: Funnel Sections, J. of Diff. Equ. 19, 270-295 (1975).
Kollaps bei "inversen" Schwingungen, uneigentliches Integral
Peter Deuflhard, Folkmar Bornemann: Numerische Mathematik, Bd. 2, Gewöhnliche Differentialgleichungen, 3. Aufl., Walter de Gruyter, Berlin, New York, 2008, S.50 f., S. 128 ff.
Runge-Kutta-Methode: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods, Aufruf am 15.03.2021.
Unfalltod
K. Eriksson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul, Bd. 2, Springer, 2013, S. 754 ff.
Planetenbahnen
Jochen Werner: Gewöhnliche Differentialgleichungen und ihre numerische Behandlung, Vorlesungsskript, Wintersemester 2001/2002, Uni Göttingen, S. 22 - 31.
K. Eriksson, D. Estep, C. Johnson: Angewande Mathematik: Body and Soul, Bd. 3, Springer, 2013, S. 901 ff.
https://de.wikipedia.org/wiki/Exzentrizit%C3%A4t_(Mathematik), Aufruf am 20.02.2021.
https://de.wikipedia.org/wiki/Merkur_(Planet), Aufruf am 20.02.2021.
Lotka-Volterra-Modell
Jochen Werner: Gewöhnliche Differentialgleichungen und ihre numerische Behandlung, Vorlesungsskript, Wintersemester 2001/2002, Uni Göttingen, S. 6 - 11.
Kermack-McKendrick-Modell
Jochen Werner: Gewöhnliche Differentialgleichungen und ihre numerische Behandlung, Vorlesungsskript, Wintersemester 2001/2002, Uni Göttingen, S. 13 f.
Wienerprozess
https://en.wikipedia.org/wiki/Wiener_process, Aufruf am 27.01
Martin Hairer: Taming Infinities, Weierstraß-Vortrag, 19. Mai 2017, Uni Paderborn.
Chi-Quadrat-Test
Donald Knuth: The Art of Computer Programming, Seminumerical Algorithms, Band 2, 3. Aufl., Addison Wesley Longman, 1998, S. 41-44.
Superspace Modell – Teichmüllerräume, Roulette
John Archibald Wheeler: Frontiers of Time, Vortrag auf der International School of Physics Enrico Fermi, Varenna, 1977.
Navier-Stokes-Gleichungen
Hölderstetigkeit
Philip Isett: Hölder Continuous Euler Flows in Three Dimensions with Compact Support in Time, 2014, https://arxiv.org/abs/1211.4065v4, Aufruf am 21.11.2020.
https://de.wikipedia.org/wiki/H%C3%B6lderstetigkeit, Aufruf am 21.11.2020.
https://en.wikipedia.org/wiki/H%C3%B6lder_condition, Aufruf am 21.11.2020.
Das allgemeine Problem
Charles L. Feffermann: Existence and Smoothness of the Navier-Stokes Equation. https://www.claymath.org/sites/default/files/navierstokes.pdf, Aufruf am 13.11.2020.
Spezielle Lösung und Regularität
Lars Onsager: Statistical hydrodynamics. Nuovo Cim, 6(S2), S. 279–287, März 1949.
Camillo De Lellis, László Székelyhidi Jr.: On turbulence and geometry: from Nash to Onsager, 8 Jan 2019. https://arxiv.org/abs/1901.02318v1, Aufruf am 13.11.2020.
László Székelyhidi: Convex integration for fluid dynamics, Vortrag auf der DMV-Jahrestagung 2020.
Sobolev-Räume
https://de.wikipedia.org/wiki/Sobolev-Raum, Aufruf am 13.11.2020.
Skalarprodukt und Hilbertraum
Die Konvergenz im quadratischen Mittel und nicht punktweise wird immer wieder in den angewandten Wissenschaften bestaunt, siehe auch die Wikipediaseite zum Gibbsschen Phänomen.
Tschebyschew-Polynome
https://en.wikipedia.org/wiki/Chebyshev_polynomials
ONS, Hilbertraum, Konvergenz
Friedrich Riesz & Béla Sz.-Nagy: Vorlesungen über Funktionalanalysis, Deutscher Verlag der Wissenschaften, Berlin, 1982.
Vektorraum
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 2.S.54 f.
Projektionsaufgabe, Einführung des Skalarproduktes
Anton Bigalke, Norbert Köhler: Mathematik, Gymnasiale Oberstufe Grundkurs 12, Brandenburg, Cornelsen, 2020, S. 48, 64 ff.
Koordiantensysteme
Griesel, H. et. Al: Elemente der Mathematik, NRW, Westermann, 2017, S. 153 f.
Manin, Yuri: Mathematik und Physik, e-enterprise, 2017, S. 31.
Lilas Wellen- und Katastrophenmathematik, Track Transition Curve
David H. von Seggern: CRC handbook of mathematical curves and surfaces. CRC Press, 2. Aufl. 1990, S. 86 f. S. 150 f., S. 208 f., S. 148 f.
https://en.wikipedia.org/wiki/Fresnel_integral, Aufruf am 09.09. 2020.
https://de.wikipedia.org/wiki/Augustin_Jean_Fresnel, Aufruf am 09.09. 2020.
https://de.wikipedia.org/wiki/Regel_von_de_L%E2%80%99Hospital, Aufruf am 11.09. 2020.
https://de.wikipedia.org/wiki/%C3%9Cbergangsbogen, Aufruf am 11.09. 2020.
https://en.wikipedia.org/wiki/Track_transition_curve, Aufruf am 11.09. 2020.
Dysons Spiel mit Zahlen
Freeman Dyson: Some Guesses in the Theory of Partitions. Eureka 8, S. 10-15 (1944).
A. O. L. Atkin & P. Swinnerton-Dyer: Some Properties of Partitions. Proc. London Math. Soc. (3) 4, S. 84-106 (1954).
Freeman Dyson: Missed Opportunities. Bull. of the Amer. Math. Soc, Vol. 78, Nr. 5, S. 635-652 (1972).
G. E. Andrews & F. G. Garvan: Dyson's Crank of a Partition. Bull. Amer. Soc. 18, S. 167-171 (1988).
Freeman Dyson: Playing with Numbers. IAS, Princton, USA, https://www.ictp.it/media/1867024/100reasons-Dyson.pdf, Aufruf am 06.08.2020.
Freeman Dyson: Maker of Patterns: An Autobiography Through Letters. Liveright Publishing, 2018.
Analysis und Wirtschaftsmathematik
Beweisidee für den Satz von Weierstraß nach:
Paul Günther et al.: Grundkurs Analysis I, Teubner, Leipzig, 1972, S. 161.
Mathematik für eine Tonmeisterin
Frequenzen der Musikinstrumente
http://www.flutepage.de/deutsch/goodies/physik.php, Aufruf am 14.07.2020
https://de.wikipedia.org/wiki/Stimmen_einer_Gitarre, Aufruf am 14.07.2020
https://www.physikalische-schulexperimente.de/physo/Frequenz_und_Wellenl%C3%A4ngen_einer_Fl%C3%B6te, Aufruf am 14.07.2020
Wellengleichung
Jay Orear: Physik. Carl Hanser Verlag, München, Wien, 1982, S. 474 ff.
Lawrence C. Evans: Partial Differential Equations. AMS, Providence, 2. Aufl. 2010, S. 65 ff.
https://de.wikipedia.org/wiki/Wellengleichung, Aufruf am 15.07.2020
Goldener Schnitt
Dora Musielak: Sophies Diary. Author House, Bloomington, 2008, S. 118-120.
Umberto Eco: Geschichte der Schönheit. Hanser, München, Wien, 2004, S. 67.
2-Farben-Problem für pythagoreische Tripel
Marijin J. H. Heule, Oliver Kullmann, and Viktor W. Marek: Solving and Veryfying the boolean Pythagorean Triples problem via Cube-and-Conquer. Theory and Applications of Satisfiability Testing – SAT 2016, pp. 228-245. https://arxiv.org/abs/1605.00723, Aufruf am 01.07.2020
Jeremy Avigad: The Mechanization of Mathematics. Notices of AMS June/July 2018, S. 681-690.
https://en.wikipedia.org/wiki/Boolean_Pythagorean_triples_problem, Aufruf am 01.07.2020
Liste der pythagoreischen Tripel
http://www.boelte.homepage.t-online.de/seiten/pythagoreischezahlen.html, Aufruf am 01.07.2020
Weiteres zum CNF-Format
https://people.sc.fsu.edu/~jburkardt/data/cnf/cnf.html, Aufruf am 02.07.2020
Transzendente Funktionen – sin π/7
Tabellen und Formeln, Volk und Wissen, Berlin, 1994, S. 30
Rekursive Folge
Idee nach:
Kurt Meyberg, Peter Vachenauer: Höhere Mathematik 1, Springer, Berlin, Heidelberg, New York, 3. Aufl., 1995, S. 100.
Die Eulerformel
Leonard Euler: Einleitung in die Analysis des Unendlichen. Erster Teil, dt. Übersetzung, Berlin, Springer, 1885. Kap. 6 und 8.
Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, Aufg. 7. S. 125
Vladimir A. Zorich: Analysis I, Berlin, Springer, 2006, S. 285, 310 ff.
Näherung von e, KI und Kant
Heinz Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, S. 116. Aufg. 18.
Brent Mittelstadt : Principles alone cannot guarantee ethical AI, Nature Machine Intelligence, Vol. 1, November 2019, S. 501–507, www.nature.com/natmachintell, https://doi.org/10.1038/s42256-019-0114-4, Aufruf am 06.05.2020.
Eulersche Zahl e: https://de.wikipedia.org/wiki/Eulersche_Zahl, Aufruf am 06.05.2020.
Immanuel Kant: Kritik der reinen Vernunft, 1781, Anacoda. Pos. 237.
Wachstumsprozesse, Exponentialfunktionen
Die Aufgabe zum Buchenwachstum stammt aus:
Heinz Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, S. 122.
Lineares Wachstum nach:
https://www.gartenjournal.net/buche-alter, Aufruf am 30.05.2020
Angaben zum Größenwachstum bei Buchen findet man bei:
https://de.wikipedia.org/wiki/Rotbuche#Gestalt_und_Wuchs, Aufruf am 22.05.2020
Texas Instruments: TI-84 Plus Benutzerhandbuch, 2010, S. 52, S. 427. https://education.ti.com/guides, 17.04.2020
Wolfgang Gregor Stagl: Versuche zur Prägung bei phytophagen Insekten: Das Fraß- und Eiablageverhalten von Gastrophysea viridula Leg. Wien, 1973. https://www.zoologicalbulletin.de/BzB_Volumes/Volume_29_1_2_3/222_241_BZB29_1_2_3_Stagl_WolfgangG.PDF
13.04.2020
https://de.wikipedia.org/wiki/Gr%C3%BCner_Sauerampferk%C3%A4fer
13.04.2020
Berechnung von √2 durch Bisektion. In: K. Erikson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul, Vol. 1, Springer, Berlin, Heidelberg, 2004, S. 204-208.
https://de.wikipedia.org/wiki/Differenzenquotient, 05.05.2020
Texas Instruments: TI-84 Plus Benutzerhandbuch, 2010, S. 52, https://education.ti.com/guides, 17.04.2020
Heinz Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, S. 111, 124.
Komplexe Sinus- und Kosinusfunktionen
Die Aufgabe stammt aus:
Reidt-Wolff: Die Elemente der Mathematik, Bd. 3- Oberstufe, Arithmetik, Algebra und Analysis. Schöningh Paderborn, 1961, S. 344 f.
Die Berechnung der neuen Eiszeit, Gletschermodelle, schwache Lösungen, Differenzengleichung, Transportgleichung
Clément Mouhot: Linear Transport Equations, Skript, 2010. https://cmouhot.files.wordpress.com/2010/01/chapter3.pdf Aufruf am 1.4.2020
Franck Boyer, Pierre Fabrie: Mathematical Tools for the Study of the Incompressible Navier-Stokes, Springer, 2013.
Daten zum Hintereisferner und Foto :
Daniel Schrott: Flächenhafte Modellierung der Energie- und Massenbilanz am Hintereisferner: das Haushaltsjahr 2003/04, Diplomarbeit, Institut für Meteorologie und Geophysik, Leopold-Franzens-Universität, Innsbruck 2006.
Differenzenschema und Stabilitätsbedingung:
Martin Burger: Numerik partieller Differentialgleichungen, Institut für Numerische und Angewandte Mathematik, Uni Münster, Wintersemester 2006/07, S. 11-14.
Unstetiges Beispiel der linearen Transportgleichung, Existenz und Eigenschaften schwacher Lösungen:
Arne Roggensack: Low Mach number equations with a heat source on networks. Modelling and analysis, Diss., Universität Hamburg, 2014, S. 55.
Theorie schwacher Lösungen:
R. J. DiPerna, P.L. Lions: Ordinary differential equations, transport theory and Sobolev spaces. Invent. math. 98, 511-547 (1989).
Fabien Maussion et al.: The Open Global Glacier Model (OGGM) v1.1. Geosci. Model Dev., 12, 909–931, 2019. https://doi.org/10.5194/gmd-12-909-2019, Aufruf am 16.01.2019.
https://de.wikipedia.org/wiki/Gletscherdynamik, Aufruf am 21.02.2019.
Gletscher, Größe und Höhe: https://de.wikipedia.org/wiki/Gletscher, Aufruf am 3.11.2019.
Eisbildung, Dichte: https://www.geo.fu-berlin.de/v/pg-net/geomorphologie/glazialmorphologie/Gletscher/Eisbildung/index.html, Aufruf am 3.11.2019.
https://wgms.ch/products_ref_glaciers/hintereisferner-alps/
Aufruf am 28.01.2020.
https://wgms.ch/latest-glacier-mass-balance-data/
Aufruf am 31.01.2020.
Die linearen Gleichungen wurde mit einem Tool auf https://www.arndt-bruenner.de/mathe/scripts/gleichungssysteme.htm berechnet, Stand vom 29.01.2020.
Unglückliche Matheaufgabe im Schulbuch:
A. Bigalke, N. Köhler: Mathematik, Gymnasiale Oberstufe 11 in Brandenburg, Cornelsen, Berlin, 2019, S. 364.
Pendel
https://en.wikipedia.org/wiki/Pendulum_(mathematics), Aufruf am 09.12.2019
https://en.wikipedia.org/wiki/Elliptic_integral, Aufruf am 01.01.2020
Lars Grüne: Numerische Methoden für Gewöhnliche Differentialgleichungen, Skript, Uni Bayreuth, 2010, S. 12 ff., S. 25 ff. u. S. 136 ff.
Runge-Kutta-Verfahren: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods, Aufruf am 11.12.2019
Laplacian-based Network Embedding
Gregorio Alanis-Lobato, Pablo Mier & Miguel A. Andrade-Navarro: Efficient embedding of complex networks to hyperbolic space via their Laplacian. Sci. Rep. 6, 30108; doi: 10.1038/srep30108 (2016).
Warteschlangen
Rolf H. Möhring: Computerorientierte Mathematik I mit Java, Manuskript, TU Berlin, WS 2009/10, S. 102.
Juraj Hromkovič, Tobias Kohn: einfach Informatik – Programmieren, Klett, 2018.
Hyperbolische Geometrie
Marián Boguñá, Fragkiskos Papadopoulos & Dmitri Krioukov: Sustaining the Internet with hyperbolic mapping. Nature Communications, Vol. 162 (2010), S. 1-8.
Was die Welt im Innersten zusammenhält
Johann Wolfgang von Goethe: Faust: Eine Tragödie. 1808, Zitat von https://gutenberg.spiegel.de/buch/faust-eine-tragodie-3664/4
Aufruf am 18.09.2019
Lawrence C. Evans: Partial Differential Equations. American Mathematical Society, 2. Aufl. 2010, S. 21.
Hans Triebel: Höhere Analysis. Deutscher Verlag der Wissenschaften, Berlin, 1972, S. 599.
Zum Weiterlesen über Linearität:
Yuri I. Manin: Mathematik und Physik, Mathematik als Metapher Bd. 3, e-enterprise, 2017, S. 26-42.
Die Berliner Tunnelaufgabe
Mathe-Abiaufgaben 2019
https://www.tagesspiegel.de/downloads/24309422/1/abi-berlin.pdf
Simplon-Tunnel
https://upload.wikimedia.org/wikipedia/commons/4/4d/Simplon_Sudportal.jpg
Höhenprofil
https://upload.wikimedia.org/wikipedia/commons/a/a6/Simplontunnel.png
Aufrufe aller dieser am 17.08.2019
I. N. Bronstein, K.A. Semendjajew: Taschenbuch der Mathematik, Teubner, Stuttgart, Leipzig, Nauka, Moskau, 25. Aufl., 1991, S. 229 f.
Autobahnaufgabe
A. Bigalke, N. Köhler: Mathematik, Gymnasiale Oberstufe 11 in Brandenburg, Cornelsen, Berlin, 2019, S. 236
Doppelter Zufall
Kevin Hartnett: Random Surfaces Hide an Intricate Order, Quanta Magazine, vom 2. 07.2019,
https://www.quantamagazine.org/random-surfaces-hide-an-intricate-order-20190702/, Aufruf am 19.08.2019
Joachim Wedekind: Codierte Kunst, Tübingen, 2018, S. 171
Diskrete Faltung
https://en.wikipedia.org/wiki/Kernel_(image_processing), Aufruf am 04.08.2019
Faltung in Adobe Photoshop: http://ian-albert.com/old/custom_filters/, Aufruf am 04.08.2019
Fermat-Zahlen
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 2, 7, 579.
Die Primfaktorzerlegung erfolgte mit https://www.mathepower.com/primfaktor.php, Aufruf am 15.07.2019.
Für die größte bekannte Fermat-Primzahl siehe https://en.wikipedia.org/wiki/Fermat_number#Factorization_of_Fermat_numbers, Aufruf am 02.08.2019
Pépin-Test: https://en.wikipedia.org/wiki/P%C3%A9pin%27s_test, Aufruf am 10.08.2019.
Rekonstruktion von Bildern
Niloy Mitra, Iasonas Kokkinos, Paul Guerrero, Vladimir Kim, Kostas Rematas, Tobias Ritschel: Deep Learning for Graphics and Geometry Processing, Part 4: Supervised Applications, Vortrag auf der Eurographics 2018. http://geometry.cs.ucl.ac.uk/dl_for_CG/, Aufruf am 30.06.2019
David Eigen, Rob Fergus: Predicting Depth, Surface Normalsand Semantic Labels with a Common Multi-Scale Convolutional Architecture, ICCV 2015.
Zufallszahlen und CG
Idee nach: Donald Knuth: The Art of Computer Programming, Seminumerical Algorithms, Vol. 2, Addison Wesley Longman, 1997, S. 2
Zufallszahlen
Donald Knuth: The Art of Computer Programming, Seminumerical Algorithms, Vol. 2, Addison Wesley Longman, 1997, S. 10-17.
Zufallszahlentest
Heuristische Zufallszahlen, ebda. ÜA S. 6-7
Kritik an der Kongruenz-Methode:
https://de.wikipedia.org/wiki/Kongruenzgenerator#M%C3%A4ngel_der_erzeugten_Zahlen
https://de.wikipedia.org/wiki/Mersenne-Twister
Aufruf am 08.06.2019
Primzahlen
https://de.wikibooks.org/wiki/Primzahlen:_Tabelle_der_Primzahlen_(2_-_100.000)
Aufruf am 08.06.2019
TigerJython
www.tigerjython.ch, Aufruf am 25.04.2019
Liste aller Befehle: http://www.tigerjython.ch/index.php?inhalt_links=navigation.inc.php&inhalt_mitte=turtle/turtledoc.html, Aufruf am 17.06.2019
Juraj Hromkovič, Tobias Kohn: einfach Informatik – Programmieren, Klett, 2018.
Datenbanken: Ebda., S. 117.
Volkslauf-Beispiel: Ebda. S. 120
Neuronale Netze
Kevin Hartnett: Foundations Built for a General Theory of Neural Networks. Qunata Magazin, 31. 01. 2019, https://www.quantamagazine.org/foundations-built-for-a-general-theory-of-neural-networks-20190131/. Aufruf am 17.04.2019.
David Rolnick, Max Tegmark: The power of deeper networks for expressing natural functions, 2018, https://arxiv.org/pdf/1705.05502. Aufruf am 17.04.2019.
Henry W. Lin, Max Tegmark, and David Rolnick: Why does deep and cheap learning work so well? 2017, https://arxiv.org/pdf/1608.08225v4, Aufruf am 08.05.2019.
Satz von Bayes: https://de.wikipedia.org/wiki/Satz_von_Bayes, Aufruf am 08.05.2019.
Weierstrass' Approximationssatz: https://en.wikipedia.org/wiki/Stone%E2%80%93Weierstrass_theorem, Aufruf am 08.05.2019.
Bubble Sort Party
Donald Knuth: The Art of Computer Programming, Sorting and Searching, Addison-Wesley, 1998, S. 105 ff.
Der Zauberlehrling
Das Gedicht stammt von Goethe. Hier die Originalversion: https://de.wikisource.org/wiki/Der_Zauberlehrling_(1798), Aufruf am 14.04.2019.
Für die Abbildung des Goethe-Denkmals im Titelbild benutzte Oliver Hinzmann das Bild von © Bwag/Wikimedia auf https://de.wikipedia.org/wiki/Liste_der_Goethedenkm%C3%A4ler#/media/File:Wien_-_Goethedenkmal_(2).JPG als Vorlage.
Markus Gabriel: Schlauer als jeder Mensch? FAZ, 21.05.2018
https://www.faz.net/aktuell/wirtschaft/kuenstliche-intelligenz/kuenstliche-intelligenz-schlauer-als-jeder-mensch-15598222.html?premium, Aufruf am 20.03.2019.
Shannon-Formel für Buchstaben bei "Effi Briest"
Textvorlagen
Theodor Fontane: Effi Briest, Berlin, 1896. http://www.gutenberg.org/ebooks/5323, Aufruf am 2.3.2017
Alex Eskin, Maryam Mirzakhani: Invariant and stationary measures for the SL(2,R) action on Moduli space, https://arxiv.org/pdf/1302.3320.pdf, Aufruf am 31.03.2019.
Ludwig Wittgenstein: Tractatus logico-philosophicus, http://tractatus-online.appspot.com/Tractatus/jonathan/D.html, Aufruf am 31.03.2019.
Die Kunst des Programmierens
Donald Knuth: The Art of Computer Programming, Vol. 1, Addison Wesley Longman, 1997. S. 2 ff.
Maschinelles Lernen
https://www.nature.com/articles/s42256-018-0002-3.pdf, 05.03.2019.
Mathematische Gitter und Restklassen
Akshay Venkatesh: What Information Might the Topology of Locally Symmetric Spaces Contain? 2018. https://www.ias.edu/ideas/venkatesh-locally-symmetric-spaces (Aufruf am 26.02.2019)
Smith-Diagramm
https://de.wikipedia.org/wiki/Komplexe_Wechselstromrechnung
https://de.wikipedia.org/wiki/Leistungsanpassung
18.02.2019
Mathematisches Billard
Nach:
Marco Bettinaglio, Ferdinando Lehmann: Mathematisches Billard. Zwei Vorschläge zu projektartigem Unterricht, ETH Zürich, 1997, online hier.
Beim gleichseitigen Dreieck ist ihnen ein kleiner Fehler unterlaufen, sie schreiben
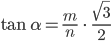
statt
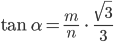
Komplexe Früchte
Hans Triebel: Analysis und mathematische Physik, Leipzig, 1981, S. 154 f.
Möbiustransformation
Das Beispiel stammt aus:
http://www2.math.uni-wuppertal.de/~fritzsch/lectures/geo/ge_k4b.pdf
Allgemeine Theorie komplexer Funktionen:
I. I. Priwalow: Einführung in die Theorie komplexer Veränderlicher, Moskau, 1983 (in Ru). S. 108 ff.
P. Günther, K. Beyer, S. Gottwald, V. Wünsch: Grundkurs Analysis, 1974, Teubner, S. 157 ff.
Retardierte Dgln
Alfred Döblin: Berlin Alexanderplatz. Die Geschichte vom Franz Biberkopf, Deutscher Taschenbuchverlag München, 48. Aufl. 2009, S. 99-100
Stefan Kretzmar, Nils Weber: Hölleluja!: Warum Handball der absolute Wahnsinn ist, Edel Books, Hamburg, 2018.
https://de.wikipedia.org/wiki/Retardierte_Differentialgleichung, Aufruf am 07.01.2019
Die Headerbilder dazu benutzen ein Foto von Alexander auf http://galerie.designnation.de/bild/44063, Aufruf am 07.01.2019.
Permutationen
Nach Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 189-190.
Logarithmische Kosmetikwerbung
Séduction #3/2018, Beilage der Süddeutschen Zeitung vom 17.11.2018
Quellen für weitere Preise
Valmont, Augenpflege
https://www.mehr-kosmetik-shop.de/valmont/pflege-augenringe.traenensaecke/
Hublot Big bang one click
https://www.hublot.com/de/kollektion/big-bang/big-bang-one-click-pink-sapphire-diamonds-39mm
Shalimar Guerlain
https://www.douglas.de/productbrand_091700.html?trac=+de.07x.guerlain..listing.cc.000009
Korrigan, lubin
https://www.meinduft.de/lubin-korrigan.html?gclid=EAIaIQobChMIpaqpsuGQ3wIVB-d3Ch30mAIjEAYYAiABEgKjvfD_BwE
Castaña Cloon Keen Atelier (2011)
https://www.jangeorge.com/products/cloon-keen-eau-de-parfums?variant=12442658734177
Dior J'adore
https://www.douglas.de/D%25C3%25BCfte-Damend%25C3%25BCfte-D%25C3%25BCfte-DIOR-J%E2%80%99adore_product_019720.html
Aufruf aller dieser am 09.12.2018
Bruttoinlandsprodukt
https://de.wikipedia.org/wiki/Liste_der_L%C3%A4nder_nach_Bruttoinlandsprodukt_pro_Kopf
Aufruf am 15.12.2018
Kamera-Charakteristik
Orhan Pamuk: Balkon, Steidl, 2018.
Jochem Berlemann: Audiovisuelle Produktion, e-enterprise, 2014, S. 123.
Marlene Schnelle-Schneyder: Sehen und Photographieren – Von der Ästhetik zum Bild, Springer, 2003, S. 138.
Weiterführende Literatur zum Zonensystem
Anselm Adam: The Negative, Little, Brown and Company, 13. Aufl. 2007.
Chris Johnson: The Practical Zone System for Film and Digital Photography, Focal Press, 4. Aufl. 2007.
Phil Davis: Beyond the Zone System, Focal Press, 4. Aufl. , 1999.
Detlef Möllering, Peter C. Slansky: Handbuch der professionellen Videoaufnahme, edition Filmwerkstatt, 1993.
Graphische Liebe
Die Euler-Charakteristik steht auf:
https://en.wikipedia.org/wiki/Euler_characteristic, Aufruf am 17.11.2018.
Mersenne-Zahlen
https://de.wikipedia.org/wiki/Mersenne-Zahl
https://www.mersenne.org/ Aufruf von beiden am 09.11.2018
https://www.mersenne.org/primes/?press=M82589933, Aufruf am 26.12.2018.
Evelyn Lamb: The Largest Known Prime Number. In: Mircea Pitici (Hrsg.) The Best Writing on Mathematics 2017, Princeton University Press, Princeton, Oxford, S. 7-9.
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 3.
Kachujin ... lineare Überlagerung von Gesichtern
Kim Hyeongwoo, Pablo Garrido, Ayush Tewari, Weipeng Xu, Justus Thies, et al.: Deep Video Portraits, ACM Trans. Graph., Vol. 37, No. 4, Article 163. Publication date: August 2018, arXiv:1805.11714v1 und Christian Theobalt: Vortrag auf der FMX 2018, Stuttgart am 27.4.2018.
3D-Models: maximo.com, 04.11.2018
3D-Rekonstruktion
Siehe auch, insbesondere fürs Bewegtbild:
Michael Zollhöfer, Patrick Stotko, Andreas Görlitz, Christian Theobalt, Matthias Nießner, Reinhard Klein, Andreas Kolb: State of the Art on 3D Reconstruction with RGB-D Cameras. In: K. Hildebrandt and C. Theobalt (Guest Editors): EUROGRAPHICS 2018, Volume 37 (2018), Number 2, STAR – State of The Art Report.
Christian Theobalt: Capturing and Editing Models of the Real World in Motion, Vortrag auf der FMX 2018, Stuttgart am 27.4.2018.
Ramanujan-Test
Die Anekdote steht auf https://en.wikipedia.org/wiki/Srinivasa_Ramanujan, Aufruf am 19.10.2018.
Schopenhauer
Arthur Schopenhauer: Die Welt als Wille und Vorstellung, Brockhaus, Leipzig, 1844. S. 143 ff.
https://opacplus.bsb-muenchen.de/Vta2/bsb10927136/bsb:BV011177450?page=13, Aufruf am 06.10.2018.
Pythagoreische Tripel
https://de.wikipedia.org/wiki/Pythagoreisches_Tripel
Antrittsvorlesung von Prof. Peter Scholze: https://www.youtube.com/watch?v=NdgQQfQLtWw, Aufruf beider am 5.10.2018
Kunst und Mathematik
https://en.wikipedia.org/wiki/Reynolds_transport_theorem, Aufruf am 22.09.2018
Genie-Kurve
Lu Liu et al.: Hot Streakes in artistic, cultural, and scientific careers, Nature vol. 559, S. 396-399 (2018).
Männer-tötendes Gift
Titelbild: © Madboy74, Drosophila melanogaster, Creative Commons CC0 1.0, https://de.wikipedia.org/wiki/Drosophila_melanogaster
Toshiyuki Harumoto & Bruno Lemaitre: Male-killing toxin in a bacterial symbiont of Drosophila, Nature 557, S. 252-255 (2018).
Handball-Wurfübung
Die Übung (mit einem Tennisball) stammt aus:
www.blv-nachwuchs.ch/service/Ball06.pdf, S. 4, Aufruf am 15.08.2018.
Torsion
Ignaz Urban: Monographia Loasacearum, Abhandlungen der Kaiserlichen Leopoldinisch-Carolinischen Deutschen Akademie der Naturforscher, Bd. 76, Halle, 1900.
L. D. Landau, E. M. Lifschitz: Lehrbuch der theoretischen Physik, Bd. VII, Elastizitätstheorie, Berlin, 1975, S. 73 ff.
Blaualgen
A. P. Belov, J. D. Giles: Dynamical model of buoyant cyanobacteria, Hydrobiologia 349: S. 87–97, 1997.
Ziomara P. Gerdtzen, J. Cristian Salgado, Axel Osses, Juan A. Asenjo, Ivan Rapaport, Barbara A. Andrews: Modeling heterocyst pattern formation in cyanobacteria, BMC Bioinformatics 2009, 10 (Suppl 6):S16, https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-10-S6-S16, Aufruf am 01.08.2018
G. Sudhakar, B. Jyothi, V. Venkateswarlu: Impact of paper mill effluents on the distribution of Cyanobacteria in the river Godavari, India, Waste Management, Vol. 11, S. 263-269, 1991
Hyun-Seob Song, William R. Cannon, Alexander S. Beliaev, Allan Konopka: Mathematical Modeling of Microbial Community Dynamics: A Methodological Review, Processes 2014, 2, 711-752; doi: 10.3390/pr2040711
S.A. Kulasooriya, D.N. Magana-Arachchi: Nitrogen fixing cyanobacteria: their diversity, ecology and utilisation with special reference to rice cultivation, J. Natn. Sci. Foundation Sri Lanka 2016 44 (2): S. 111-128.
Hans W. Paerl, Valerie J. Paul: Climate change: Links to global expansion of harmful cyanobacteria, water research 46 (2012) S. 1349 - 1363, https://www.sciencedirect.com/science/article/pii/S0043135411004386, Aufruf am 01.08.2018
Über Blaualgen in populären Medien
https://www.mdr.de/brisant/badeseen-ostsee-kueste-blaualgen-gefahren-100.html,
https://www.sueddeutsche.de/politik/blaualgen-die-schattenseite-des-sommers-1.4075022
https://www.zdf.de/nachrichten/heute-19-uhr/blaualgen-vermehren-sich-rasant-100.html
Alle diese wurden am 01.08.2018 aufgerufen.
Wie Apfelsinen natürlich trianguliert werden
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 152ff.
https://de.wikipedia.org/wiki/Euler-Charakteristik, Aufruf am 21.07.2018
Wie der Hirschwurz-Haarstrang mathematisiert wird
Zum Hirschwurz siehe https://de.wikipedia.org/wiki/Hirschwurz-Haarstrang, Aufruf am 15.07.2018
Wie Polynomnäherungen Verwirrung stiften können
Masashi Soga, Kevin J. Gaston: Extinction of experience: evidence, consequences and challenges of loss of human-nature interactions, Front. Ecol. Environ. 14, S. 94-101 (2016)
S. R. Rintoul, et al: Choosing the future of Antarctica, Nature Vol. 558, S. 233-241, 14. Juni 2018
Arndt Brunner: https://www.arndt-bruenner.de/mathe/scripts/gleichungssysteme.htm, Aufruf am 07.07.2018.
Lösung eines linearen Gleichungssystems: http://wims.unice.fr/wims/, Aufruf am 07.07.2018
Wie Natur, Kunst und Mathematik zusammenhängen
Bildungsgesetz der goldenen Spirale
https://en.wikipedia.org/wiki/Golden_spiral, Aufruf am 02.07.2018.
2. Ableitung bei Polarkoordinaten
I. N. Bronstein, K. A. Semendjajew: Taschenbuch der Mathematik, Teubner & Nauka, 1991, S. 283 f.
Raue Oberflächen
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 537 ff.
Andrea Weidlich (Weta Digital): Thinking in Layers - Material Modelling in a Modern Rendering Pipeline, Vortrag am 25.04.2018, FMX 2018, Stuttgart.
Dylan Sisson (Pixar): Latest Developments in Pixar's RenderMan, Vortrag am 25.04.2018, FMX 2018, Stuttgart.
https://en.wikipedia.org/wiki/Specular_highlight, Aufruf am 18.06. 2018.
Positionssysteme mit negativer Basis
Jerzy Dreszer: Mathematik-Handbuch für Technik und Naturwissenschaft, Leipzig, 1975, S.19 f.
Reelle Zahlen
Carl Friedrich Gauß: Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik. Springer, Berlin, 1889, http://resolver.sub.uni-goettingen.de/purl?PPN373456743, Aufruf am 26.5.2018
E. Schwerdtfeger: Trainingsbuch Algebra, Verlag Europa-Lehrmittel, 2017, S. 84 f.
Ganze Zahlen
The Univalent Foundations Program: Quotients. In: Homotopy Type Theory, Institute for Advanced Study, 2013, S. 261 ff.
Eugen Schwerdtfeger: Trainingsbuch Algebra, Verlag Europa-Lehrmittel, 2017, S. 16.
Vollständige Induktion
Wolfgang Sartorius von Waltershausen: Gauss zum Gedächtniss. S. Hirzel, Leipzig, 1856, S. 12–13.
Linus Kramer: Was ist Mathe? In: Sira Busch: Was ist Mathe? http://summa.stiftungrechnen.de/was-ist-mathe/, Aufruf am 13.5.2018.
Gaußsche Summenformel: https://de.wikipedia.org/wiki/Gau%C3%9Fsche_Summenformel, Aufruf am 13.5.2018.
Rudolf vom Hofe, Bernhard Humpert, Heinz Griesel, Helmut Postel: Mathematik heute 9. Mittelschule/Oberschule Sachsen Hauptschulbildungsgang, Bildungshaus Schulbildungsverlage, Braunschweig, 2016, S. 182.
Terme und Umformungen
The Univalent Foundations Program: The natural numbers. In: Homotopy Type Theory, Institute for Advanced Study, 2013, S. 49.
Yuri Manin: Gödels Theorem. In: Mathematik als Metapher, e-enterprise, 2016, S. 237-272
Eugen Schwerdtfeger: Trainingsbuch Algebra, Verlag Europa-Lehrmittel, 2017, S. 7, 10, 11.
Feuerwehrfunktion
Christoph Berg, Julian Brüggemann, Bertold Heinrich et al.: Mathematik Technik – Fachoberschulreife, Cornelsen, Berlin, 2015, S. 56 f.
Gauß-Algorithmus
ebda. S. 22.
Dgln in der 10. Klasse
V. I. Arnold: Gewöhnliche Differentialgleichungen, Berlin, 1979, S. 23 f.
H. Griesel, H. Postel, R. v. Hofe: Mathematik heute 10, Regelschule Thüringen, Schroedel, 2014, S. 113.
Horizont als Zufallsweg
Kevin Hartnett: A Unified Theory of Randomness. In: Mircea Pitici (Hrsg.): The Best Writings in Mathematics 2017, Princeton University Press, Princeton und Oxford, S. 10-23.
Jason Miller, Scott Sheffield, Wendelin Werner: Non-simple SLE curves are not determined by their range. arxiv:1609.04799v3, 2018.
Steffen Rohde, Oded Schramm: Basic properties of SLE, arxiv:math/0106036v4, 2004.
Wiener Prozess: https://de.wikipedia.org/wiki/Wiener-Prozess, Aufruf am 31.03.2018.
Hausdorff-Dimension: https://de.wikipedia.org/wiki/Hausdorff-Dimension, Aufruf am 31.03.2018
Van der Corput-, Halton- und Hammersleyfolgen
https://en.wikipedia.org/wiki/Low-discrepancy_sequence , Aufruf am 25.05.2018.
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 443 ff.
Harald Niederreiter: Random Number Generation and Quasi-Monte Carlo Methods, SIAM, Philadelphia, 1992.
Hawkings schwarze Löcher
Nach: S. W. Hawking: Into a Black Hole, http://www.hawking.org.uk/into-a-black-hole.html, Aufruf am 21.3.2018
S. W. Hawking: Virtual Black Holes, https://arxiv.org/pdf/hep-th/9510029.pdf, Aufruf am 21.3.2018
Kontinuumshypothese I und II
Zum Weiterlesen für Teil I:
Yuri I. Manin: Georg Cantor und sein Erbe. In: Mathematik als Metapher, e-enterprise, 2016, S. 207-232.
Rationale und reelle Zahlen, rationaler Zahlenstrahl:
K. Erikson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul, Vol. 1, Springer, Berlin, Heidelberg, 2004, S. 201-215.
Axiomensystem reeller Zahlen:
Vladimir A. Zorich: Analysis I, Springer, Berlin, Heidelberg, 2006, S. 38-82.
Paul Cohen: Wie ich »Forcing« entdeckte, e-enterprise, Lemgo, 2017, S. 126-128.
Übersetzung von:
Paul Cohen: The Discovery of Forcing, Rocky Mountain Journal of Mathematics, Vol. 32 (4), 2002, S. 1071-1100.
Im Zitat ist vermutlich gemeint:
Paul Cohen: Set Theory and the Cotinuum Hypothesis, New York, Benjamin, 1963.
Parakonsistente Logik
Alain Badiou, Gilles Haéri: Lob der Mathematik, Passagen Verlag, 2018, S. 60 f.
Alain Badiou: Logic of Worlds, Being and Event 2, continuum, 2009, S. 166 ff.
Bild an der Wand nach: Tamfang: H2checkers_2ii.png auf https://en.wikipedia.org/wiki/Triangle_group#/media/File:H2checkers_2ii.png, auf dem Tisch nach: Anton Sherwood: File:H2checkers 34i.png auf https://en.wikipedia.org/wiki/File:H2checkers_34i.png, alle beide am 03.03.2018 aufgerufen, sowie nach dem Muster vom letzten Beitrag von Tamfang, H2checkers_iii.
Mehrwertige Logik: Wie mehrwertige Logik Mathematik 4.0 einleitet In: Mathezartbitter 2015-2017, 25. Beitrag, e-enterprise, 2017.
Hyperbolische Parkettierung
Für das Poincare-Disk-Modell, siehe https://en.wikipedia.org/wiki/Poincar%C3%A9_disk_model
https://en.wikipedia.org/wiki/Uniform_tilings_in_hyperbolic_plane
Tamfang: H2checkers iii.png, siehe: https://commons.wikimedia.org/wiki/File:H2checkers_iii.png
Alle Aufrufe am 26.02.2018.
Wie Antonija die beste hyperbolische Idee hat. In: Mathezartbitter 2015-2017, 66. Beitrag, e-enterprise, 2017.
Bullet Time Setup
Bewegungsstudie nach https://whitelines.com/, Aufruf am 16.02.2018.
Tensoren
Lucien Hardy: On The Theory of Composition in Physics, arXiv:1303.1537v2, 2013.
Philip Ball: A World without cause and effect, Nature Vol. 546, S. 590-592, 29. 6. 2017.
Magdalena Zych, Fabio Costa, Igor Pikovski, Timothy C. Ralph, Caslav Brukner: General relativistic effects in quantum interference of photons, arXiv:1206.0965v2, 2012.
Michael Reed, Barry Simon: Methods of Modern Mathematical Physics, Academic Press, Rev. Edition, 1980, S. 49-53.
Yuri I. Manin: Mathematik und Physik, e-enterprise, 2017, S. 117-119.
Prozentrechnung
H. Athen, H. Griesel: Mathematik heute 7 für Gymnasien in Baden-Württemberg, Schroedel, Hannover, 1979, S. 7, 12.
Negativer Index of Refraction
Fresnelsche Formeln
https://en.wikipedia.org/wiki/Fresnel_equations, Aufruf am 18.1.2018
IOR
https://en.wikipedia.org/wiki/List_of_refractive_indices, Aufruf am 18.1.2018
Circe of Confusion
Nach: The Thin Lens Model and Depth of Fields. In: Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 368-375.
Für weitere Infos zum DoF siehe:
Jochem Berlemann: Audiovisuelle Produktion. 2. Aufl., e-enterprise, 2014.
Dunkirk-Zeittransformationen
Nolan-Interview:
Christopher Nolan explains the 'audio illusion' that created the unique music in 'Dunkirk', http://www.businessinsider.de/dunkirk-music-christopher-nolan-hans-zimmer-2017-7?r=UK&IR=T, Aufruf am 1.1.2017.
Topologische Begriffe:
Michael Reed, Barry Simon: Methods of Modern Mathematical Physics, Academic Press, Rev. Edition, 1980.
Dunkirk-Struktur
Filminfos, Bilder:
https://www.rottentomatoes.com/m/dunkirk_2017/#&gid=1&pid=n-1764181
https://www.warnerbros.com/dunkirk
http://www.dunkirkmovie.com/
Aufruf am 17.12.2017.
Joshua Levine: Dunkirk, The History Behind the Major Motion Picture, William Collins, 2017.
Nolan-Interview:
https://www.dga.org/Craft/DGAQ/All-Articles/1703-Summer-2017/WWII-Dunkirk.aspx,
Aufruf am 17.12.2017.
Infos zur Geschichte der Evakuierung:
https://de.wikipedia.org/wiki/Dunkirk_(2017)
https://en.wikipedia.org/wiki/Dunkirk_(2017_film)
https://de.wikipedia.org/wiki/Operation_Dynamo
Churchills Rede:
https://www.youtube.com/watch?v=1Okt_YrKPdw
https://www.winstonchurchill.org/resources/speeches/1940-the-finest-hour/we-shall-fight-on-the-beaches/
Aufruf aller dieser am 28.12.2017.
Kameramodelle
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 82, 355ff., 378.
Rendergleichung
Das mathematische Modell stammt aus: A. A. Penzov, I. T. Dimov, L. Szirmay-Kalos, V. N. Koylazov: Analysis of the Monte Carlo Image Creation by Uniform Separation. In: I. Lirkov, S. Margenov, and J. Wa´sniewski (Hsgb.): LSSC 2009, LNCS 5910, S. 419–426, 2010, Springer-Verlag Berlin Heidelberg 2010.
James T. Kajiya: The Rendering Equation. Siggraph 1986, ACM 0-89791-196-2/86/008/0143
Reelle Zahlen
https://en.wikipedia.org/wiki/Real_number, Aufruf am 4.11.2017
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 2.
Vladimir A. Zorich: Analysis I, Springer, 2006, S. 38ff.
Jean Dieudonné: Grundzüge der modernen Analysis, Vieweg, 1985, S. 29 ff.
Linkin Park: Crawling, Musik/Text: Chester Bennington, Rob Bourdon, Brad Delson, Joseph Hahn, Mike Shinoda. In: Hybrid Theory, Warner Bros. Records Inc. , 2000.