Was die Welt im Innersten zusammenhält

Jenny hat Lila eingeladen, ihr ihre Uni zu zeigen.

Lila Wie bist Du mit Deinem Mathestudium zufrieden?

Jenny Weißt Du, wir haben viele mathematische Fächer und Wahlmöglichkeiten, ich könnte Dir von allen erzählen, ein paar Anekdoten von den Profs und von uns Studis, aber das ist ja nicht das Wichtigste. Ich habe für mich entdeckt, dass die meisten Vorlesungen axiomatisch aufgebaut sind:

Mathematik im Kleinen

In der Analysis fängt man mit Zahlen, Folgen, Reihen an, dann Funktionen, ihre Ableitung und Integrale. Das geht ziemlich straight forward, ohne groß nach Zahlen oder Folgen selbst zu fragen, als wollte der Prof nur den Grenzwert definieren. Als der Grenzwertbegriff dann an der Tafel stand, haben seine Augen richtig geleuchtet. Als wäre er einen Berg hinaufgeklettert und angekommen. Aber kaum waren wir beim Grenzwert angenommen, ging es zum Nächsten. Als läuft er uns davon und wir hinterher. Nur jetzt im Sommer habe ich mal Gelegenheit, über alles nachzudenken. Kennst Du das:

Ob mir durch Geistes Kraft und Mund
Nicht manch Geheimnis würde kund;
Daß ich nicht mehr mit saurem Schweiß
Zu sagen brauche, was ich nicht weiß;
Daß ich erkenne, was die Welt
Im Innersten zusammenhält...

Lila Goethes Faust!

Jenny Du kennst Du das!

Lila Ja klar, Goethes Faust – wir hatten das in der Schule, das ist für mich ein Stück Deutschland. Mit Max habe ich über den Zauberlehrling gesprochen. Goethe ist echt cool – und so zeitlos!

Jenny In der Algebra geht es mit Mengen, Gruppen, Ringen, Körpern, Abbildungen und Vektorräumen los. Das bleibt ziemlich abstrakt. Anfangs habe ich mich gar nicht 'reingefunden, weil das algebraische Denken so anders ist. Das habe ich Dir ja schon erzählt. Später Funktionalanalysis, lineare Operatoren in Hilbert- und Banach-Räumen, Distributionen, Sobolew-Räume für partielle Differentialgleichungen usw. Jedes Fach wird für sich allein entwickelt. Es wird immer abstrakter; und ich hatte nicht das Gefühl, dass alles zusammenhängt.

Lila Und wie weit bist Du gekommen – mit Deiner Philosophie über Mathematik?

Linearität im Großen

Jenny Ich habe gemerkt, dass wir immer wieder lineare Strukturen verwenden. In der linearen Algebra sowieso, da haben wir meist mit endlich dimensionalen linearen Räumen zu tun, aber auch in der Analysis gibt es lineare Räume. Das sind unendlich dimensionale Funktionenräume. Bei den Differentialgleichungen haben wir lineare gelöst, die Lösungen haben wieder lineare Strukturen, bei den linearen partiellen ebenso.

Linearität

Lila Was ist eine lineare Struktur?

Jenny Im einfachsten Fall ist das ein Zahlbereich, wo die Addition erklärt ist, zum Beispiel die ganzen Zahlen bilden eine Gruppe bzgl. der Addition.

Die ganzen Zahlen als additive Gruppe. 0 ist das 1-Element.

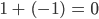
Das ist die einfachste Struktur. Dann gibt es lineare Räume wie den R³: Da drin hast Du Vektoren. Hier!

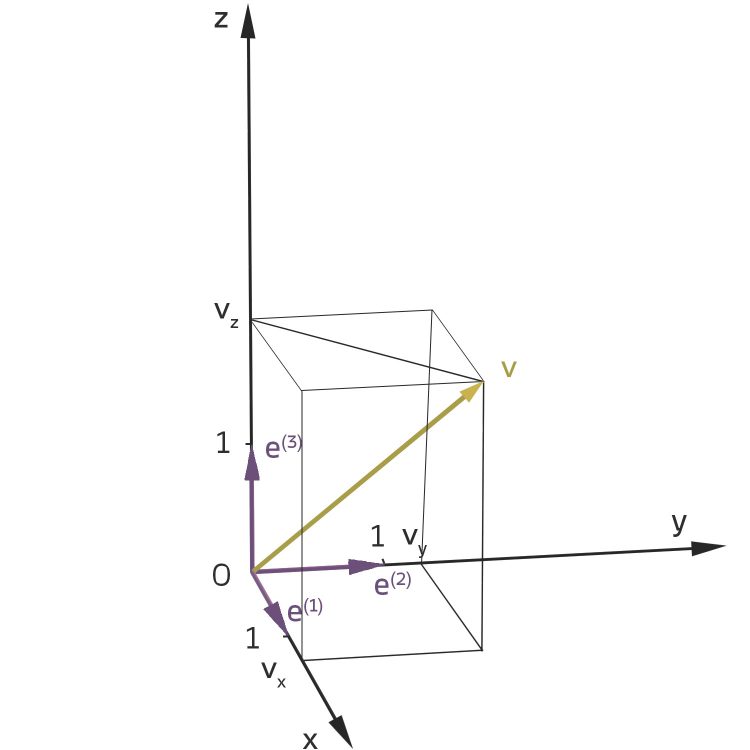
koordinaten_cam_03_14-04 — Darstellung eines Vektors v durch 3 Einheitsvektoren im 3-dimenisionalen Vektorraum

Du kannst mit den Vektoren e⁽¹⁾, e⁽²⁾ und e⁽³⁾ alle Positionen v im Raum beschreiben:

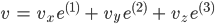
Mit den 3 Koordinaten (v_x , v_y, v_z) kannst Du v festlegen. Durch Summenbildung und Vielfache erhältst Du alle Punkte im Raum. Linearität ist, wenn die Summe 2er Elemente aus einem Raum V wieder in V liegt, wie auch das α-Fache:

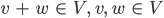
α ist eine Zahl.

Lila Klar, ich verstehe.

Jenny Gut, dann mache ich mal weiter. Wenn Du einen Punkt im Raum hast, dann kannst Du ihm eine Temperatur zuordnen. Oder auch eine Konzentration oder was anderes. Sagen wir mal,

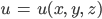
Lass mich das mal eindimensional zeichnen. So könnte eine Temperaturverteilung aussehen:

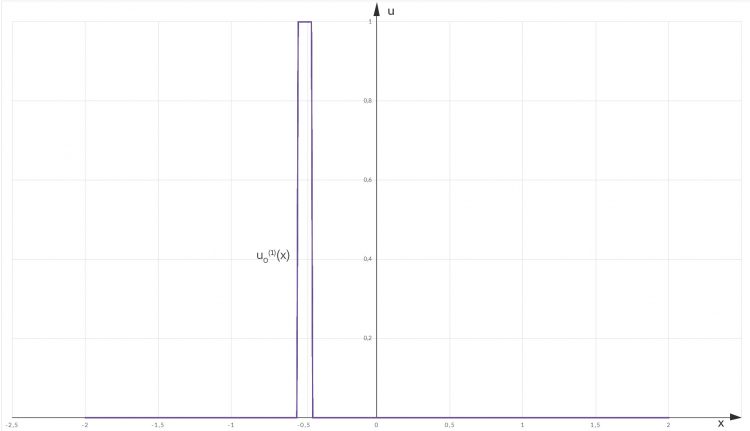
IV_32_waermeleitung_u01_08 — Funktion u₀⁽¹⁾(x) zur Beschreibung einer Temperatur in Abhängigkeit vom Ort x.

Solche stetigen Funktionen bilden wieder einen linearen Raum, einen Funktionen-Raum. Du kannst darin addieren und Vielfache bilden. Dieser Raum ist jetzt so ein unendlich dimensionaler Funktionenraum.

Lila Okay, finde ich gut, dass man darin addieren kann.

Wärmeleitungsgleichung

Jenny Schließlich hast Du die Wärmeleitungsgleichung:

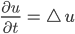
Lila Was ist das für eine Formel?

Jenny Die linke Seite steht für die Änderung mit der Zeit, die rechte Seite steht für eine Diffusion. Das Dreieck ist der Laplace-Operator. Er steht für die Summe der örtlichen 2. Ableitungen:

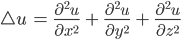
Das ist das fouriersche Gesetz zur Ausbreitung von Wärme. Ich habe mal alle Koeffizienten 1 gesetzt.

Lila Aha!

Jenny Jetzt nehmen wir mal eine Temperaturverteilung zur Zeit t = 0, das nennt sich Anfangswertproblem. Diese hier, u₀⁽¹⁾, die beschreibt zum Beispiel, dass es in einem Intervall recht heiß ist, sonst kalt. So eine Art Kochplatte. Dann gibt es eine LÖsungsformel, um die Temperaturverteilung zu einer anderen Zeit t auszurechnen. Das ist gar nicht selbstverständlich, aber für die Wärmeleitug gibt es eine lineare Vorschrift.

Lila Ach – wie sich die Kochplatte abkühlt und wie die Umgebung wärmer wird?

Jenny Genau, die geht so:

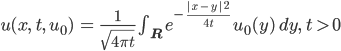
Lila Sag mal, die Exponentialfunktion kann ich gut berechnen. Aber wie kann man das Integral ausrechnen?

Jenny Da gibt es keine Stammfunktion.

Integralnäherung

Lila Kann man das Integral numerisch annähern? I mean - ohne Grenzwert?

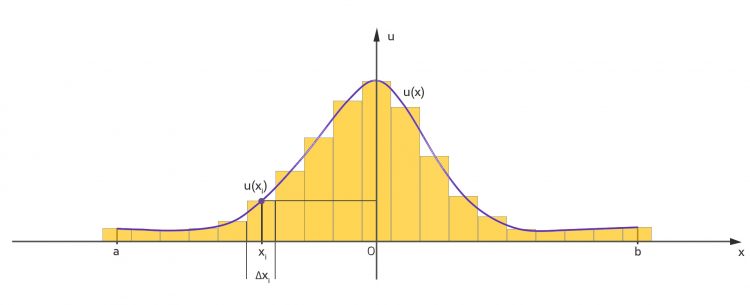
Jenny Hmm, statt des Integrals nehmen wir die Summe der Funktionswerte

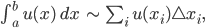
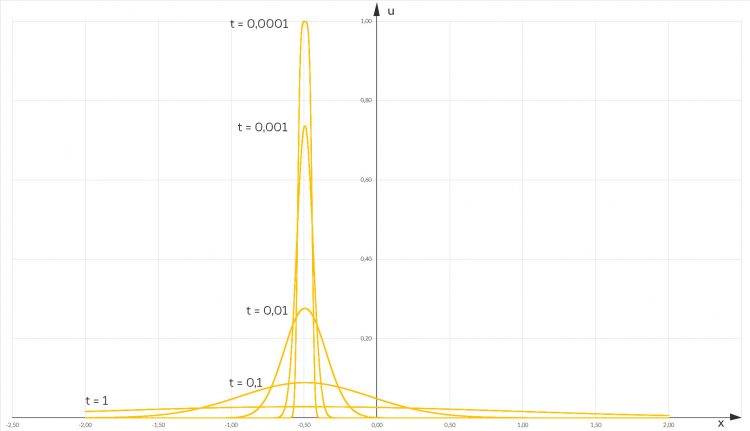
dabei ist 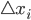die Länge des Intervalls auf der x-Achse.

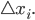
IV_32_integral_08 — Einfache Näherung der Fläche unter der Kurve u(x) durch die gelbe Fläche- Diese besteht aus Rechtecken mit den Höhen u(x_i) und Breiten

Einfache Näherung der Fläche unter der Kurve u(x) durch die gelbe Fläche- Diese besteht aus Rechtecken mit den Höhen u(x_i) und Breiten

Numerische Lösung der Wärmeleitungsgleichung für 1 Kochplatte

Lila Hey, das kann ich Dir ausrechnen! Das brauche ich nicht einmal eine Programmierumgebung, das geht mit einem einfachen Tabellenkalkulationsprogramm! Hier:

IV_32_waermeleitung_06 — Numerische Lösung der Wärmeleitungsgleichung mit obiger Anfangsverteilung u₀⁽¹⁾

Jenny Lila, Du bist toll! Du hast die Formel konstruktiv gemacht!

Lila Und wie ist das nun mit dem Linearen?

Jenny Die Lösungsformel ist linear in u₀.

Lila ????

Jenny Wenn wir die Wärmeleitungslösungsformel nehmen und für 2 verschiedene Anfangswerte addieren:

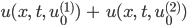
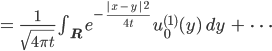
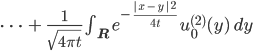
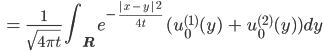
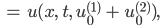
dann können wir dieselbe Lösungsformel für die Summe der Anfangswere nehmen. Das funktioniert wegen der Linearität des Integrals.

Lila Ooh!

Jenny Stell Dir vor, wir hätten eine 2. Anfangsbedingung , ähnlich wie unsere 1., lass sie uns einfach an der u-Achse spiegeln, dann könnten wir wieder die Lösung für verschiedenen Zeiten t ausrechnen.

Lila Eine andere Kochplatte?

Jenny Genau!

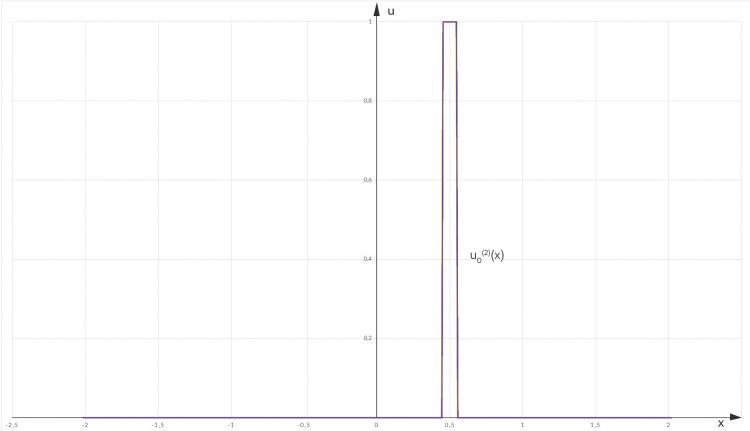
IV_32_waermeleitung_u02_09 — Zweite Anfangsbedingung u₀⁽²⁾(x).

Lila Dann komm diesselbe Lösung raus, nur gespiegelt, ist ja klar.

Numerische Lösung der Wärmeleitungsgleichung für 2 Kochplatten

Jenny Wenn wir jetzt beide Kochplatten anstellen, kriegen wie eine Lösung, die ist dann die Summe der beiden einzelnen Lösungen. So geht Linearität!

Lila Das probiere ich mal. Das wäre die Summe der Anfangswerte:

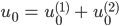
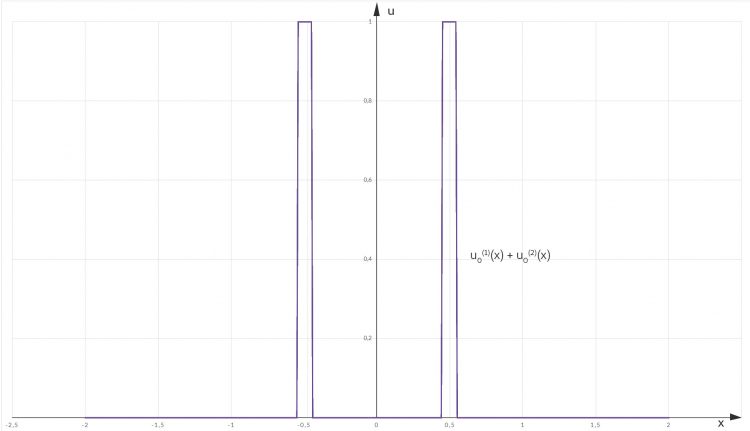
IV_32_waermeleitung_summe_u0_08 — Anfangsbedingung für die Wärmeleitungsgleichung zur Zeit t = 0 – die Summe der beiden Anfangswerte u₀⁽¹⁾(x) und u₀⁽²⁾(x).

Jenny Stimmt!

Lila Okay, warte, das geht jetzt ganz schnell!

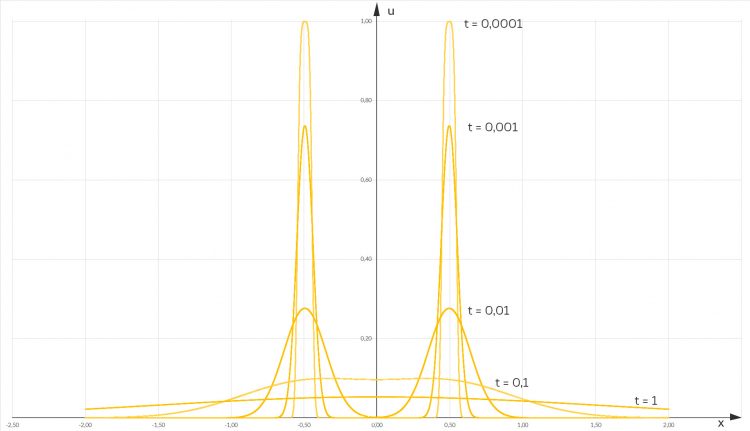
IV_32_waermeleitung_summe_06 — Numerische Lösung für die Anfangsbedingung aus u₀⁽¹⁾(x) + u₀⁽²⁾(x).

Jenny Cool!

Lila Diese Linearität ist wirklich etwas, was die Welt im Innersten zusammenhält!

Jenny Ja.

***

Verständnisfragen

Wie sehen Anfangswerte für Situationen aus, wo es nicht um die Ausbreitung von Wärme sondern um Kälte geht? Gilt da auch die Wärmeleitungsgleichung?

Lösungen

Zum Beispiel wäre 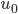ein Anfangswert für eine kleine kalte Stelle in einer sonst warmen Umgebung:

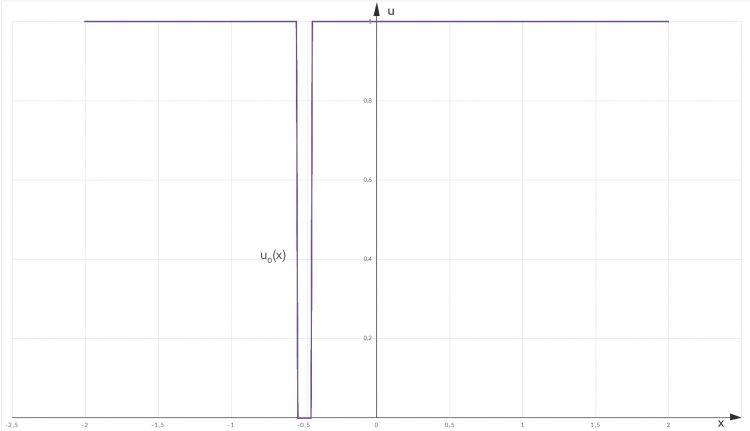
IV_32_kaelteleitung_awa_08 — Anfangswert mit einer "kalten" Stelle

Die Wärmeleitungsgleichung kann für beliebige Funktionen (mit gewissen Regularitätseigenschaften, zB Stetigkeit) als Anfangswert (AW) angewendet werden. Sie kann für nichtnegative Funktionen als Wärme interpretiert werden. Lösung für diesen AW:

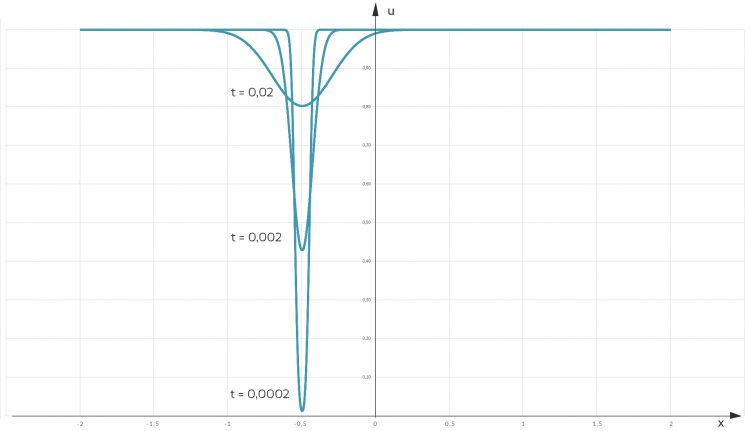
Numerische Lösung der Wäremleitungsgleichung für den obigen AW

Solche Lösungen kann man kaum als Kältewellen bezeichnen.