Wie schön pythagoreische Tripel sind

Rike steht am Abend nach getaner Arbeit am Fenster ihres Apartments. Es regnet. Endlich ein Abend für sich selbst. Dann schaut sie ein bisschen im Netz und kommt immer wieder zu den diesjährigen Preisträgern der Fields-Medaille. Sie freut sich für Peter Scholze und bewundert ihn. Vielleicht ist heute der Abend gekommen, ihn zu verstehen?

Parametrische Lösung für die pythagoreischen Tripel

Sie schaut sich seine Antrittsvorlesung an und versucht, alles zu verstehen. Als er über den großen Fermatschen Satz spricht, möchte sie, so wie er die ganzen Zahlen und Eigenschaften von ihnen verstehen. So ist bekannt, dass es unendlich viele ganzzahlige Lösungen x, y, z für

x² + y² = z²

gibt. Diese kann man konstruieren, in dem man für beliebige ganzzahlige, positive Zahlen u und v, u > v, die Zahlen des Tripels x, y und z wie folgt berechnet:

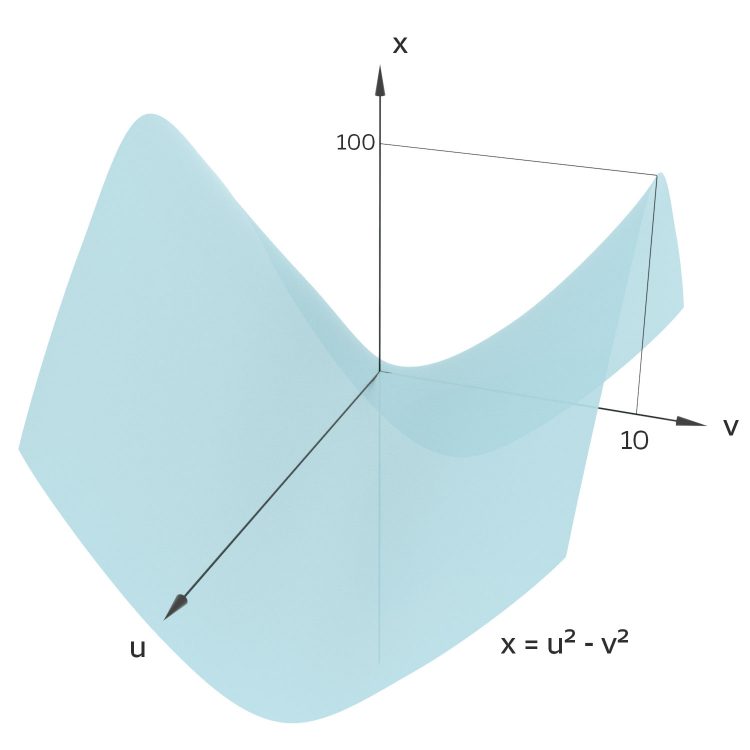
x = u² - v²

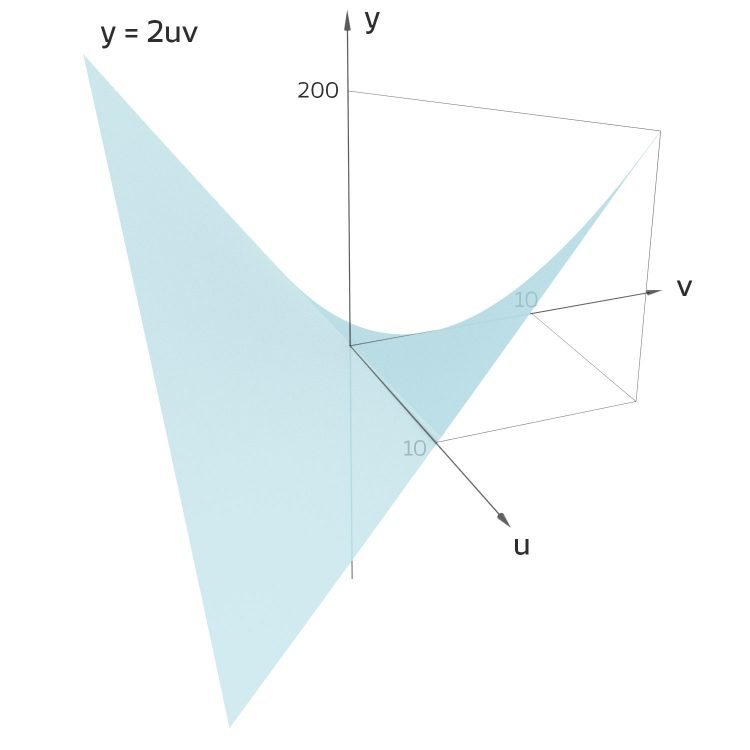
y = 2uv

z = u² + v².

x-Koordinate

Für die erste Funktion x = x(u, v) erhält man einen sogenannten Sattel.

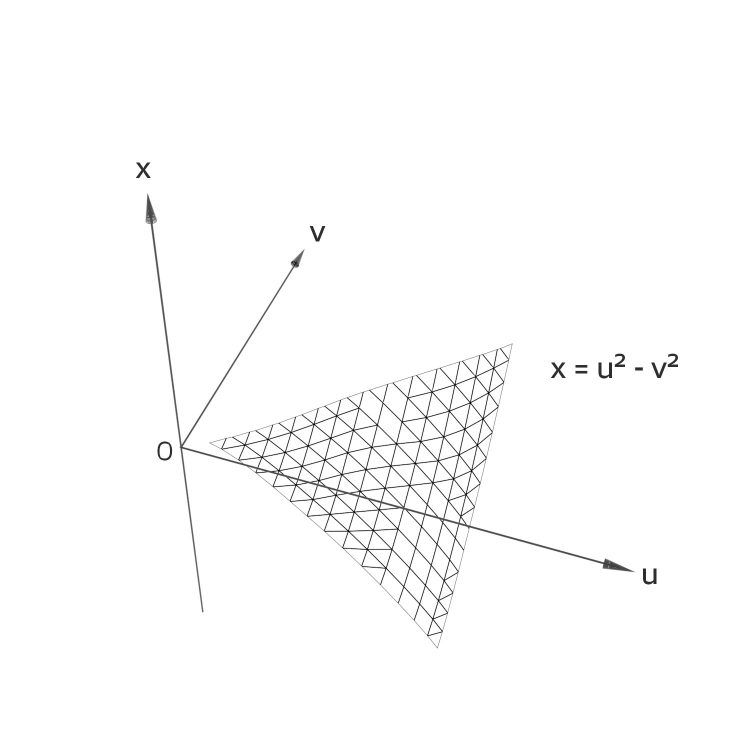
Für die Tripel nehmen wir nur einen Teil der Fläche: die positiven, ganzen Zahlen u und v, u > v, und nur die Punkte, wo sich die Gitterlinien schneiden.

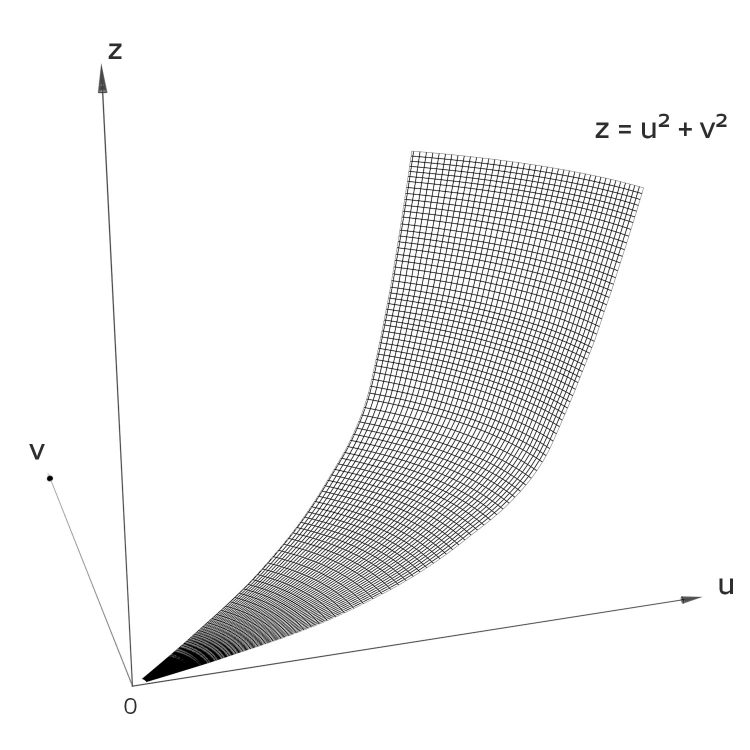
y-Koordinate

Für y = 2uv erhält man die Fläche, die in Null auch einen Sattel hat:

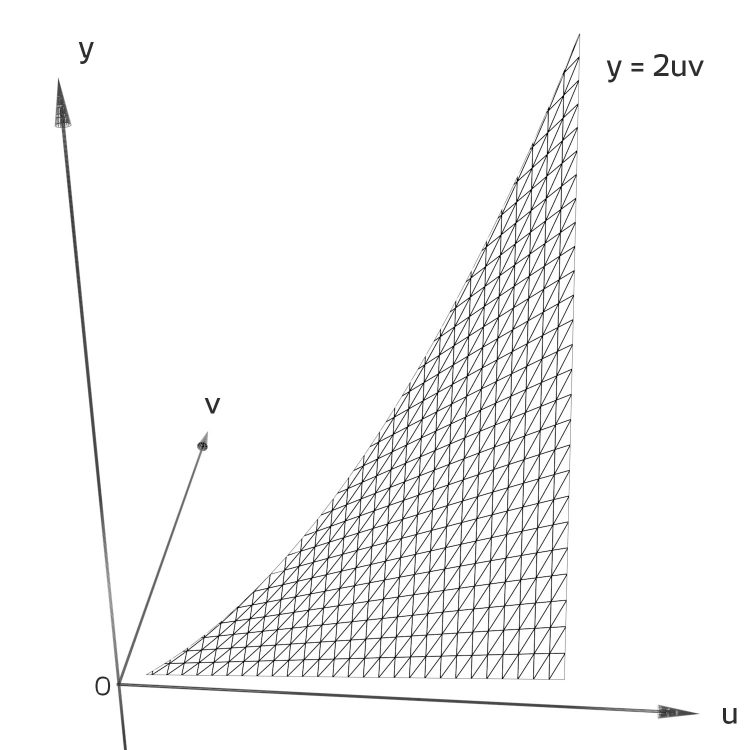
und für ganze Zahlen u > v >0 sieht das so aus:

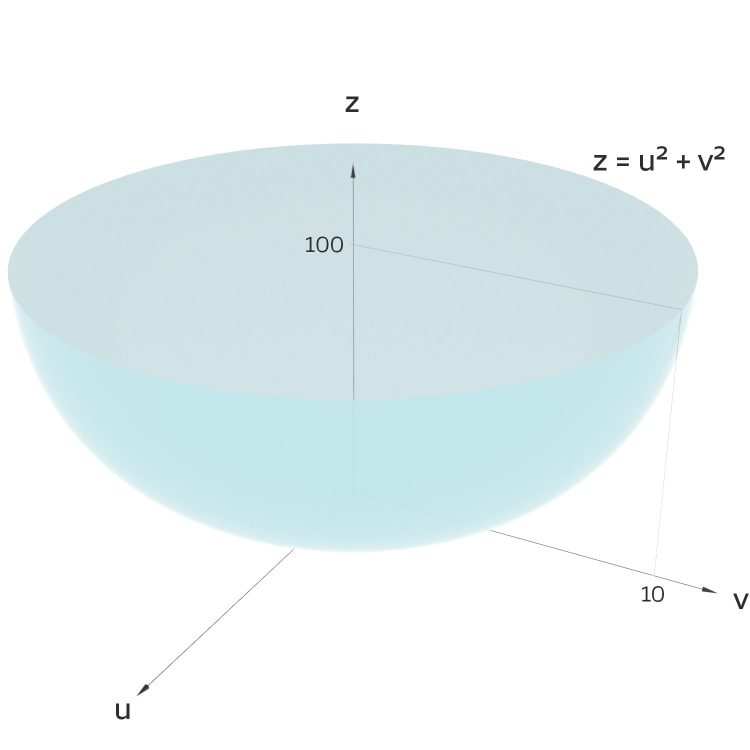
z-Koordinate

Für z = u² + v² erhält man eine "Tasse":

Davon sind für die Tripel-Konstruktion nur die Schnittpunkte des Gitters zugelassen:

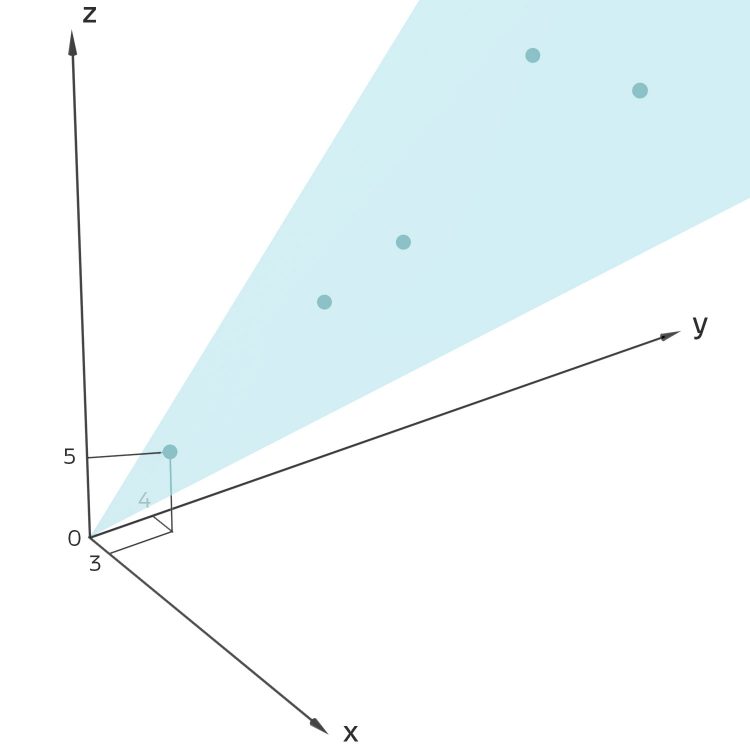
Die kleinsten Tripel

So erhält man für

u = 2, v = 1:

x = u² - v² = 2² - 1² = 3,

y = 2uv = 2 · 2 · 1 = 4,

z = u² + v² = 2²+1² = 5,

also

P = (3, 4, 5),

das ist das erste Tripel.

Primitive Tripel

Rike überlegt, wenn sie dieses Tripel P = (x, y, z) gefunden hat, so sind auch Vielfache (x · k, y · k, z · k) dieser Zahlen Lösungen der Gleichung

x² + y² = z²,

das heißt, schon aus (3, 4, 5) kann sie durch Vielfache davon

(3k, 4k, 5k), k ganze Zahl,

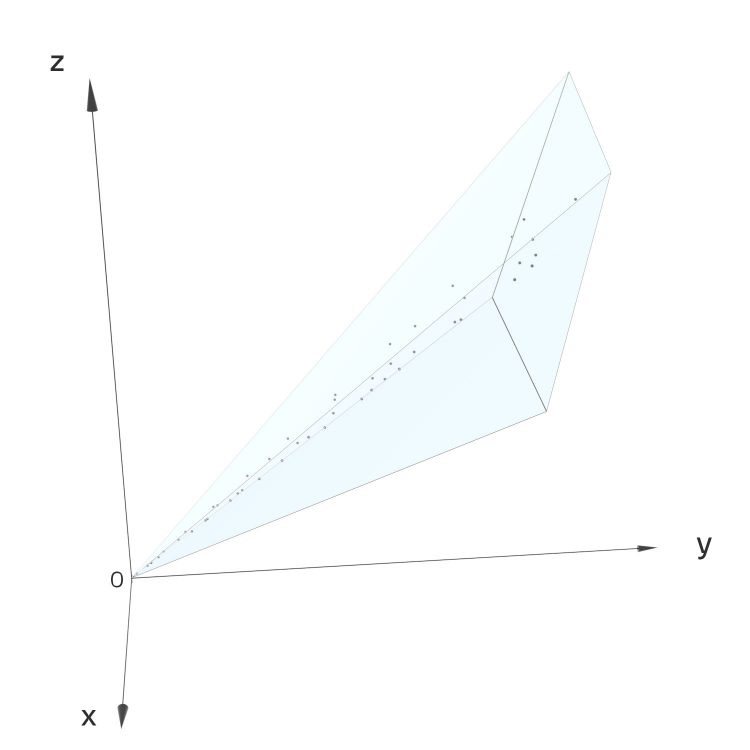
unendlich viele Lösungen finden. Diese liegen auf einer Gerade im 3D-Raum. Um solche "trivialen" Tripel auszuschließen, hat man den Begriff der primitiven Tripel geschaffen, das sind solche, die keinen gemeinsamen Teiler haben. Rike zeichnet die ersten 47 primitiven Tripel, ihr gefällt die Struktur, die sie bilden. Sie könnte beinahe Zahlentheoretikerin werden, aber nur beinahe.

***

Übungsaufgaben

1. Überprüfe, ob die parametrischen Flächen x = u² - v², y = 2uv, z= u² + v² tatsächlich x² + y² = z² lösen.
2. Was passiert, wenn u und v beide ungerade sind?

Lösungenen

1. OK
2. Dann sind x, y und z gerade, also ist das Tripel (x, y, z) nicht primitiv.