Ski-Thema
Charlys Skiflugaufgabe
Die Formel zur Fluglänge stammt von LEIFIphysik, Joachim Herz Stiftung, Hamburg, 06.06.2024.
Informationen zu Skisprungschanzen und dem Konstruktionspunkt wurden von Wikipedia benutzt, 06.06.2024.
Das Titelbild wurde von Stability AI erzeugt, Prompt: “a fantasy landscape with a sportsman ski flying in a lot of white, blue and little orange colors, digital art” und Benutzung einer schematischen Abb. einer Skischanze von Wikipedia, siehe ebenda. Abb. erzeugt am 04.06.2024 und danach von M.E. bearbeitet.
Dieses Bild von einer Skifahrerin wurde ebenfalls von Stability AI erzeugt, Prompt: "a winter landscape with a girl on ski trails and mountains in a lot of white, blue and little orange colors", 02.05.2024 und danach von M.E. bearbeitet.
Die unglaubliche Skipiste
Das Titelbild wurde von Stability AI erzeugt, Prompt: “A fantasy skiing hall in a lot of white, blue and little orange, digital art” und Vorlage einer Profilkurve; das Skifahrerbild: ebenso, Prompt: "A small skiing hall in a lot of white, blue and little orange", beide vom 06.05.2024 und danach von M.E. bearbeitet.
Newtons Original und Rikes Anwendung
Isaak Newton: Fluxes (ca. 1665-1700). Method of Curves and Infinite Series, and application to the Geometry of Curves. Cambridge University Library, https://cudl.lib.cam.ac.uk/view/MS-ADD-03960/327, Rechte: ebenda bzw. direkt am Bild: https://images.lib.cam.ac.uk/content/images/MS-ADD-03960-014-00003.jpg, Aufruf vom 16.04. 2024.
Das Titelbild wurde von Stability AI erzeugt, Prompt: “professor with very long gray hair without beard before a fantasy winter landscape with big mountains in a lot of white, blue and some orange colors, 150 years ago”, 10.04.2024, danach von M.E. bearbeitet
Trainingsstrecken-Aufgaben
Aufgabe und Lösung stammen aus:
Mathematik Abitur 2024. Leistungskurs. Berlin und Brandenburg. Prüfungen und Lösungen, L&K development GmbH, Berlin, 2023, S. 43 ff., S. 112 ff.
Mathematical Image Analysis Group: Das Newton-Verfahren, mia.uni-saarland.de, Universität des Saarlandes, letzter Aufruf am 05.04.2024.
Bigalke, Anton; Köhler, Norbert (Hrsgb.): Mathematik. Band 1. Analysis, Cornelsen Verlag, Berlin, 2013, S. 124 ff. Das Zitat stammt von S. 125. Das Beispiel zur Quadratwurzel ist auf S. 128.
fx-570EX, FX-991EX User's Guide, CASIO COMPUTER CO., LTD., Tokio/Norderstedt, 2015, S. 19. casio-manual.pdf, letzter Aufruf am 18.04.2024
Das Titelbild wurde von Stability AI erzeugt, Prompt: “A boy and girl with ski running in a great landscape..., digital art”, 02.04.2024, und danach von M.E. bearbeitet
Das Titelbild für Teil 2: Die Entfernung der besten Skipiste zum Mittelpunkt der Erde wurde ebenfalls von Stability AI erzeugt, Prompt: “a fantasy winter landscape with ski trail in white, blue and little orange colors..., digital art”, 03.04.2024, danach von M.E. bearbeitet
Das Titelbild für Teil 3: Rikes Begegnung mit Newton wurde ebenfalls von Stability AI erzeugt, Prompt: “a young man with long gray hair, beardless in front of a fantasy winter landscape with big mountains in a lot of white, blue and some orange colors,” und Vorlage des Newton-Porträts von Godfrey Kneller, 10.04.2024, danach von M.E. bearbeitet
Splines
de.wikipedia.org/wiki/Spline-Interpolation, Aufruf am 26.05.202.
en.wikipedia.org/wiki/Spline_interpolation, Aufruf am 26.05.202.
Für Anwendungen in der Computergrafik siehe:
Eric Lengyel: Mathematics for 3D Game Programming and Computer Graphics, 3. Aufl., Course Technology, 2012, S. 317-359.
Die schräge Ellipsenaufgabe
Roland Ott, Wolfgang Schomburg: Abitur 2022. Aufgabensammlung zur zentralen schriftlichen Abiturprüfung Berlin/Brandenburg Mathematik, Merkur Verlag Rinteln, 4. Aufl. 2021, S. 203.
Bob Blume: Tötet ChatGPT das Lernen? https://bobblume.de/2022/12/14/toetet-chatgpt-das-lernen/, Aufruf am 15.05.202.
AI-generierte Bilder
Aditya Ramesh, Prafulla Dhariwal, Alex Nichol, Casey Chu, Mark Chen: Hierarchical Text-Conditional Image Generation with CLIP Latents, https://arxiv.org/abs/2204.06125, Aufruf am 26.10.2022.
Chitwan Saharia, William Chan, Huiwen Chang, Chris A. Lee, Jonathan Ho, Tim Salimans, David J. Fleet, Mohammad Norouzi: Palette: Image-to-Image Diffusion Models, ACM SIGGRAPH, August 8-11, 2022, Vancouver, https://arxiv.org/abs/2111.05826, Aufruf am 26.10.2022.
Dr. Mike Pound: How AI Image Generators Work (Stable Diffusion / Dall-E) - Computerphile, https://www.youtube.com/watch?v=1CIpzeNxIhU, Aufruf am 26.10.2022.
Jonathan Ho; Ajay Jain, Pieter Abbeel: Denoising Diffusion Probabilistic Models, 34th Conference on Neural Information Processing Systems (NeurIPS 2020), Vancouver, Canada, https://arxiv.org/pdf/2006.11239.pdf, 07.12.2022.
Wiki Diffusion model: wiki/Diffusion_model, 07.12.2022
Ari Seff: What are Diffusion Models?
vom 20.04.2022, www.youtube.com
Die rot-grüne Urnenaufgabe
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, Analysis-Aufgabe von 2019, S. 38 f., S. 48 f., https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Rikes alternative Bonsai-Aufgabe
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, Analysis-Aufgabe von 2019, S. 72 f. https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Bonsais
https://bonsai.org/de/
https://www.bonsaiempire.de/grundlagen
https://www.bonsai-shop.com/bonsai/kiefern,
Aufrufe am 05.08.2022.
Die Gutschein-App
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, Stochastik-Aufgabe von 2021, S. 13, 35 f. https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Die rot-grüne Programmieraufgabe
Das Gesetz der großen Zahlen - Satz von Bernoulli, Version aus
B. W. Gnedenko: Lehrbuch der Wahrscheinlichkeitsrechnung, Berlin, 1979, S. 189.
Die rot-grüne Würfelaufgabe
Abiaufgabe darin
Mathematik Abitur 2022, Grundkurs, Berlin Brandenburg, S. 44, 64 f. https://www.abitur-berlin.de/mathe/pruefungsheft-2022, Aufruf am 01.05.2022.
Zum Wahrscheinlichkeitsbegriff und -auffassungen
Stuart J. Russell; Peter Norvig: Artificial Intelligence. A Modern Approach, Pearson, 3. Aufl., 2016, S. 490 f.
Absurde Bevölkerungsstruktur und Freizeitverhalten
Studien zur Freizeit (leider nicht vom Autor verwendet)
https://de.statista.com/themen/64/freizeit/#topicHeader__wrapper
http://www.freizeitmonitor.de/
Abiaufgabe 2017 vom Bildungsserver Berlin-Brandenburg: https://bildungsserver.berlin-brandenburg.de/fileadmin/bbb/unterricht/pruefungen/abitur_bb/Zabi_Mathematik/17_Ma_LK_CAS_Aufgaben_neu.pdf, S. 9
Benutze Zahnarztstudie
Nele Kettler, Regine Chenot und A. Rainer Jordan: Subjektives Qualitätsverständnis von Vertragszahnärzten im Umgang mit Qualitätsmanagement- Ergebnisse eines bundesweiten Surveys von Health insurance dentists’ subjective perceptions of quality when implementing quality management in practice – results from a nationwide survey - Zeitschrift für Evidenz, Fortbildung und Qualität im Gesundheitswesen (zefq-journal.com), 2015, S. 695-703.
Yuri I. Manin, Matilde Marcolli: Semantic Spaces, 2016, Math. Comput. Sci. 10, no. 4, 2016, S. 459-477, https://arxiv.org/pdf/1605.04238.pdf
Aufruf am 18.5.2022 für alle
Sigma-Regeln und Zahnarztaufgabe
Zahnärztliche Studien
Vom Institut der Deutschen Zahnärzte:
Kassenzahnärztliche Bundesvereinigung, Geschäftsbericht 2013/2014:
https://www.kzbv.de/geschaeftsbericht-2013-2014.877.de.html
Aufruf am 1.5.2022 für alle
Potsdam, Sportschule, Bevölkerung
https://de.wikipedia.org/wiki/Sportschule_Potsdam_%E2%80%9EFriedrich_Ludwig_Jahn%E2%80%9C
https://de.wikipedia.org/wiki/Potsdam
Aufruf am 1.5.2022 für alle
Statistikaufgaben und -thoerie
bildungsserver.berlin-brandenburg, 2015, S. 9, letzter Aufruf am 08.05.2022
Norbert Henze: Stochastik für Einsteiger. Eine Einführung in die faszinierende Welt des Zufalls. 10. Aufl., Springer-Spektrum, 2013, S. 221 ff.
Anton Bigalke, Norbert Köhler (Hrsg.): Mathematik, Gymnasiale Oberstufe, Grundkurs, 12. Cornelsen, 2020, S. 210 ff.
Modell des Gebisses
von VikingDigital auf Turbosqiud.com, Aufruf am 07.05.2022
Satz von Moivre-Laplace
B. W. Gnedenko: Lehrbuch der Wahrscheinlichkeitsrechnung. Akademie-Verlag Berlin, 1979, S. 80 ff.
Wissenschaftlicher Taschenrechner von Casio
https://www.casio-schulrechner.de/de/produkte/software/classwizemulator/
https://support.casio.com/storage/de/manual/pdf/DE/004/fx-87_991DEX_DE.pdf
Aufruf am 21.04.2022 für beide
en.wikipedia.org/wiki/De_Moivre , Aufruf am 13.04.2022.
Flaubert und Python
Für das Titelbild wurde das folgende Bild von Flaubert auf Wikipedia verwendet:
https://fr.wikipedia.org/wiki/Gustave_Flaubert#/media/Fichier:Gustave-Flaubert2.jpg, Aufruf am 22.03.2022.
Mathematische Erektionen
Gustave Flaubert: Briefe. Herausgegeben und übersetzt von Helmut Scheffel, Diogenes, 1977.
Wörterbuch der Gepflogenheiten: S. 153, 223
Brief an Louise Colet: S. 224 ff.
Frz. Originaltext: S. 752
Charakter im Titelbild: Whiteclown N Hallin von Deadgnv auf mixamo.com, Pose auch von mixamo.com Aufruf am 08.03.2022.
Paulas merkwürdige Sägezahnkurve
Rike hat den RSA-Algorithmus für Max in einem 15. Beitrag unseres Blogs von 2015-2017 und einem vollständig berechneten Beispiel mit kleinem 
dargelegt, das findet sich jetzt in einem E-Book Mathezartbitter. Die Effi-Briest-Analyse ist dort ebenfalls, Beiträge 54-59.
Die neue Sichtweise auf den RSA-Algorithmus und das Beispiel mit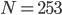 
gehen auf das folgende Buch zurück:
Johannes Buchmann: Einführung in die Krytographie, Springer, 4. Aufl., 2008
Düsseldorfer Kaffee-Aufgabe und die Methode der kleinsten Quadrate
Die Aufgabe
Standardsicherung NRW, S. 3 ff. Aufruf am 17.08.2021.
Methode der kleinsten Quadrate
https://de.wikipedia.org/wiki/Methode_der_kleinsten_Quadrate, Aufruf am 17.08.2021.
PDEs und Maschinelles Lernen
Zongyi Li et al.: Fourier Neural Operator For Parametric Partial Differential Equations, Version vom 17.05.2021, https://arxiv.org/pdf/2010.08895.pdf, Version vom 17.05.2021, Letzter Aufruf: 23.06.2021.
Anil Ananthaswamy: Latest Neural Nets Solve World’s Hardest Equations Faster Than Ever Before, Quantamagazine, Version vom 19.4.2021, https://www.quantamagazine.org/new-neural-networks-solve-hardest-equations-faster-than-ever-20210419/, Letzter Aufruf: 23.06.2021.
Jon McLoone: From Zero to AI in 60 minutes: https://www.wolfram.com/wolfram-u/machine-learning-zero-to-AI-60-minutes/ Letzter Aufruf am 20.06.2021.
Die rückwärtige Wärmeleitungsgleichung
K. Eriksson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul. Bd. 3, 2003, Heidelberg, S. 1140-1143.
A. A. Samarskij: Theorie der Differenzenverfahren, Leipzig, 1984, S. 32, 169-179.
John Archibald Wheeler: Frontiers of Time, Vortrag auf der International School of Physics Enrico Fermi, Varenna, 1977, S. 46, 134.
Integraltrichter
Peter Deufhard, Folkmar Bornemann: Numerische Mathematik 2. Gewöhnliche Differentialgleichungen, 3. Aufl., 2008, Berlin, S. 51-56.
Hellmuth Kneser: Über die Lösung eines Systems gewöhnlicher Differentialgleichungen, das der Lipschitzchen Bedingung nicht genügt, S.-B. Preuß. Akad. Wiss. Phys. Math. KI. (1923), 171-174.
Charles C. Pugh: Funnel Sections, J. of Diff. Equ. 19, 270-295 (1975).
Kollaps bei "inversen" Schwingungen, uneigentliches Integral
Peter Deuflhard, Folkmar Bornemann: Numerische Mathematik, Bd. 2, Gewöhnliche Differentialgleichungen, 3. Aufl., Walter de Gruyter, Berlin, New York, 2008, S.50 f., S. 128 ff.
Runge-Kutta-Methode: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods, Aufruf am 15.03.2021.
Unfalltod
K. Eriksson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul, Bd. 2, Springer, 2013, S. 754 ff.
Planetenbahnen
Jochen Werner: Gewöhnliche Differentialgleichungen und ihre numerische Behandlung, Vorlesungsskript, Wintersemester 2001/2002, Uni Göttingen, S. 22 - 31.
K. Eriksson, D. Estep, C. Johnson: Angewande Mathematik: Body and Soul, Bd. 3, Springer, 2013, S. 901 ff.
https://de.wikipedia.org/wiki/Exzentrizit%C3%A4t_(Mathematik), Aufruf am 20.02.2021.
https://de.wikipedia.org/wiki/Merkur_(Planet), Aufruf am 20.02.2021.
Lotka-Volterra-Modell
Jochen Werner: Gewöhnliche Differentialgleichungen und ihre numerische Behandlung, Vorlesungsskript, Wintersemester 2001/2002, Uni Göttingen, S. 6 - 11.
Kermack-McKendrick-Modell
Jochen Werner: Gewöhnliche Differentialgleichungen und ihre numerische Behandlung, Vorlesungsskript, Wintersemester 2001/2002, Uni Göttingen, S. 13 f.
Wienerprozess
https://en.wikipedia.org/wiki/Wiener_process, Aufruf am 27.01
Martin Hairer: Taming Infinities, Weierstraß-Vortrag, 19. Mai 2017, Uni Paderborn.
Chi-Quadrat-Test
Donald Knuth: The Art of Computer Programming, Seminumerical Algorithms, Band 2, 3. Aufl., Addison Wesley Longman, 1998, S. 41-44.
Superspace Modell – Teichmüllerräume, Roulette
John Archibald Wheeler: Frontiers of Time, Vortrag auf der International School of Physics Enrico Fermi, Varenna, 1977.
Navier-Stokes-Gleichungen
Hölderstetigkeit
Philip Isett: Hölder Continuous Euler Flows in Three Dimensions with Compact Support in Time, 2014, https://arxiv.org/abs/1211.4065v4, Aufruf am 21.11.2020.
https://de.wikipedia.org/wiki/H%C3%B6lderstetigkeit, Aufruf am 21.11.2020.
https://en.wikipedia.org/wiki/H%C3%B6lder_condition, Aufruf am 21.11.2020.
Das allgemeine Problem
Charles L. Feffermann: Existence and Smoothness of the Navier-Stokes Equation. https://www.claymath.org/sites/default/files/navierstokes.pdf, Aufruf am 13.11.2020.
Spezielle Lösung und Regularität
Lars Onsager: Statistical hydrodynamics. Nuovo Cim, 6(S2), S. 279–287, März 1949.
Camillo De Lellis, László Székelyhidi Jr.: On turbulence and geometry: from Nash to Onsager, 8 Jan 2019. https://arxiv.org/abs/1901.02318v1, Aufruf am 13.11.2020.
László Székelyhidi: Convex integration for fluid dynamics, Vortrag auf der DMV-Jahrestagung 2020.
Sobolev-Räume
https://de.wikipedia.org/wiki/Sobolev-Raum, Aufruf am 13.11.2020.
Skalarprodukt und Hilbertraum
Die Konvergenz im quadratischen Mittel und nicht punktweise wird immer wieder in den angewandten Wissenschaften bestaunt, siehe auch die Wikipediaseite zum Gibbsschen Phänomen.
Tschebyschew-Polynome
https://en.wikipedia.org/wiki/Chebyshev_polynomials
ONS, Hilbertraum, Konvergenz
Friedrich Riesz & Béla Sz.-Nagy: Vorlesungen über Funktionalanalysis, Deutscher Verlag der Wissenschaften, Berlin, 1982.
Vektorraum
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 2.S.54 f.
Projektionsaufgabe, Einführung des Skalarproduktes
Anton Bigalke, Norbert Köhler: Mathematik, Gymnasiale Oberstufe Grundkurs 12, Brandenburg, Cornelsen, 2020, S. 48, 64 ff.
Koordiantensysteme
Griesel, H. et. Al: Elemente der Mathematik, NRW, Westermann, 2017, S. 153 f.
Manin, Yuri: Mathematik und Physik, e-enterprise, 2017, S. 31.
Lilas Wellen- und Katastrophenmathematik, Track Transition Curve
David H. von Seggern: CRC handbook of mathematical curves and surfaces. CRC Press, 2. Aufl. 1990, S. 86 f. S. 150 f., S. 208 f., S. 148 f.
https://en.wikipedia.org/wiki/Fresnel_integral, Aufruf am 09.09. 2020.
https://de.wikipedia.org/wiki/Augustin_Jean_Fresnel, Aufruf am 09.09. 2020.
https://de.wikipedia.org/wiki/Regel_von_de_L%E2%80%99Hospital, Aufruf am 11.09. 2020.
https://de.wikipedia.org/wiki/%C3%9Cbergangsbogen, Aufruf am 11.09. 2020.
https://en.wikipedia.org/wiki/Track_transition_curve, Aufruf am 11.09. 2020.
Dysons Spiel mit Zahlen
Freeman Dyson: Some Guesses in the Theory of Partitions. Eureka 8, S. 10-15 (1944).
A. O. L. Atkin & P. Swinnerton-Dyer: Some Properties of Partitions. Proc. London Math. Soc. (3) 4, S. 84-106 (1954).
Freeman Dyson: Missed Opportunities. Bull. of the Amer. Math. Soc, Vol. 78, Nr. 5, S. 635-652 (1972).
G. E. Andrews & F. G. Garvan: Dyson's Crank of a Partition. Bull. Amer. Soc. 18, S. 167-171 (1988).
Freeman Dyson: Playing with Numbers. IAS, Princton, USA, https://www.ictp.it/media/1867024/100reasons-Dyson.pdf, Aufruf am 06.08.2020.
Freeman Dyson: Maker of Patterns: An Autobiography Through Letters. Liveright Publishing, 2018.
Analysis und Wirtschaftsmathematik
Beweisidee für den Satz von Weierstraß nach:
Paul Günther et al.: Grundkurs Analysis I, Teubner, Leipzig, 1972, S. 161.
Mathematik für eine Tonmeisterin
Frequenzen der Musikinstrumente
http://www.flutepage.de/deutsch/goodies/physik.php, Aufruf am 14.07.2020
https://de.wikipedia.org/wiki/Stimmen_einer_Gitarre, Aufruf am 14.07.2020
https://www.physikalische-schulexperimente.de/physo/Frequenz_und_Wellenl%C3%A4ngen_einer_Fl%C3%B6te, Aufruf am 14.07.2020
Wellengleichung
Jay Orear: Physik. Carl Hanser Verlag, München, Wien, 1982, S. 474 ff.
Lawrence C. Evans: Partial Differential Equations. AMS, Providence, 2. Aufl. 2010, S. 65 ff.
https://de.wikipedia.org/wiki/Wellengleichung, Aufruf am 15.07.2020
Goldener Schnitt
Dora Musielak: Sophies Diary. Author House, Bloomington, 2008, S. 118-120.
Umberto Eco: Geschichte der Schönheit. Hanser, München, Wien, 2004, S. 67.
2-Farben-Problem für pythagoreische Tripel
Marijin J. H. Heule, Oliver Kullmann, and Viktor W. Marek: Solving and Veryfying the boolean Pythagorean Triples problem via Cube-and-Conquer. Theory and Applications of Satisfiability Testing – SAT 2016, pp. 228-245. https://arxiv.org/abs/1605.00723, Aufruf am 01.07.2020
Jeremy Avigad: The Mechanization of Mathematics. Notices of AMS June/July 2018, S. 681-690.
https://en.wikipedia.org/wiki/Boolean_Pythagorean_triples_problem, Aufruf am 01.07.2020
Liste der pythagoreischen Tripel
http://www.boelte.homepage.t-online.de/seiten/pythagoreischezahlen.html, Aufruf am 01.07.2020
Weiteres zum CNF-Format
https://people.sc.fsu.edu/~jburkardt/data/cnf/cnf.html, Aufruf am 02.07.2020
Transzendente Funktionen – sin π/7
Tabellen und Formeln, Volk und Wissen, Berlin, 1994, S. 30
Rekursive Folge
Idee nach:
Kurt Meyberg, Peter Vachenauer: Höhere Mathematik 1, Springer, Berlin, Heidelberg, New York, 3. Aufl., 1995, S. 100.
Die Eulerformel
Leonard Euler: Einleitung in die Analysis des Unendlichen. Erster Teil, dt. Übersetzung, Berlin, Springer, 1885. Kap. 6 und 8.
Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, Aufg. 7. S. 125
Vladimir A. Zorich: Analysis I, Berlin, Springer, 2006, S. 285, 310 ff.
Näherung von e, KI und Kant
Heinz Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, S. 116. Aufg. 18.
Brent Mittelstadt : Principles alone cannot guarantee ethical AI, Nature Machine Intelligence, Vol. 1, November 2019, S. 501–507, www.nature.com/natmachintell, https://doi.org/10.1038/s42256-019-0114-4, Aufruf am 06.05.2020.
Eulersche Zahl e: https://de.wikipedia.org/wiki/Eulersche_Zahl, Aufruf am 06.05.2020.
Immanuel Kant: Kritik der reinen Vernunft, 1781, Anacoda. Pos. 237.
Wachstumsprozesse, Exponentialfunktionen
Die Aufgabe zum Buchenwachstum stammt aus:
Heinz Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, S. 122.
Lineares Wachstum nach:
https://www.gartenjournal.net/buche-alter, Aufruf am 30.05.2020
Angaben zum Größenwachstum bei Buchen findet man bei:
https://de.wikipedia.org/wiki/Rotbuche#Gestalt_und_Wuchs, Aufruf am 22.05.2020
Texas Instruments: TI-84 Plus Benutzerhandbuch, 2010, S. 52, S. 427. https://education.ti.com/guides, 17.04.2020
Wolfgang Gregor Stagl: Versuche zur Prägung bei phytophagen Insekten: Das Fraß- und Eiablageverhalten von Gastrophysea viridula Leg. Wien, 1973. https://www.zoologicalbulletin.de/BzB_Volumes/Volume_29_1_2_3/222_241_BZB29_1_2_3_Stagl_WolfgangG.PDF
13.04.2020
https://de.wikipedia.org/wiki/Gr%C3%BCner_Sauerampferk%C3%A4fer
13.04.2020
Berechnung von √2 durch Bisektion. In: K. Erikson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul, Vol. 1, Springer, Berlin, Heidelberg, 2004, S. 204-208.
https://de.wikipedia.org/wiki/Differenzenquotient, 05.05.2020
Texas Instruments: TI-84 Plus Benutzerhandbuch, 2010, S. 52, https://education.ti.com/guides, 17.04.2020
Heinz Griesel et al.: Elemente der Mathematik, Nordrhein-Westfalen Qualifikationsphase Grundkurs. Schroedel Westermann, 2015, S. 111, 124.
Komplexe Sinus- und Kosinusfunktionen
Die Aufgabe stammt aus:
Reidt-Wolff: Die Elemente der Mathematik, Bd. 3- Oberstufe, Arithmetik, Algebra und Analysis. Schöningh Paderborn, 1961, S. 344 f.
Die Berechnung der neuen Eiszeit, Gletschermodelle, schwache Lösungen, Differenzengleichung, Transportgleichung
Clément Mouhot: Linear Transport Equations, Skript, 2010. https://cmouhot.files.wordpress.com/2010/01/chapter3.pdf Aufruf am 1.4.2020
Franck Boyer, Pierre Fabrie: Mathematical Tools for the Study of the Incompressible Navier-Stokes, Springer, 2013.
Daten zum Hintereisferner und Foto :
Daniel Schrott: Flächenhafte Modellierung der Energie- und Massenbilanz am Hintereisferner: das Haushaltsjahr 2003/04, Diplomarbeit, Institut für Meteorologie und Geophysik, Leopold-Franzens-Universität, Innsbruck 2006.
Differenzenschema und Stabilitätsbedingung:
Martin Burger: Numerik partieller Differentialgleichungen, Institut für Numerische und Angewandte Mathematik, Uni Münster, Wintersemester 2006/07, S. 11-14.
Unstetiges Beispiel der linearen Transportgleichung, Existenz und Eigenschaften schwacher Lösungen:
Arne Roggensack: Low Mach number equations with a heat source on networks. Modelling and analysis, Diss., Universität Hamburg, 2014, S. 55.
Theorie schwacher Lösungen:
R. J. DiPerna, P.L. Lions: Ordinary differential equations, transport theory and Sobolev spaces. Invent. math. 98, 511-547 (1989).
Fabien Maussion et al.: The Open Global Glacier Model (OGGM) v1.1. Geosci. Model Dev., 12, 909–931, 2019. https://doi.org/10.5194/gmd-12-909-2019, Aufruf am 16.01.2019.
https://de.wikipedia.org/wiki/Gletscherdynamik, Aufruf am 21.02.2019.
Gletscher, Größe und Höhe: https://de.wikipedia.org/wiki/Gletscher, Aufruf am 3.11.2019.
Eisbildung, Dichte: https://www.geo.fu-berlin.de/v/pg-net/geomorphologie/glazialmorphologie/Gletscher/Eisbildung/index.html, Aufruf am 3.11.2019.
https://wgms.ch/products_ref_glaciers/hintereisferner-alps/
Aufruf am 28.01.2020.
https://wgms.ch/latest-glacier-mass-balance-data/
Aufruf am 31.01.2020.
Die linearen Gleichungen wurde mit einem Tool auf https://www.arndt-bruenner.de/mathe/scripts/gleichungssysteme.htm berechnet, Stand vom 29.01.2020.
Unglückliche Matheaufgabe im Schulbuch:
A. Bigalke, N. Köhler: Mathematik, Gymnasiale Oberstufe 11 in Brandenburg, Cornelsen, Berlin, 2019, S. 364.
Pendel
https://en.wikipedia.org/wiki/Pendulum_(mathematics), Aufruf am 09.12.2019
https://en.wikipedia.org/wiki/Elliptic_integral, Aufruf am 01.01.2020
Lars Grüne: Numerische Methoden für Gewöhnliche Differentialgleichungen, Skript, Uni Bayreuth, 2010, S. 12 ff., S. 25 ff. u. S. 136 ff.
Runge-Kutta-Verfahren: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods, Aufruf am 11.12.2019
Laplacian-based Network Embedding
Gregorio Alanis-Lobato, Pablo Mier & Miguel A. Andrade-Navarro: Efficient embedding of complex networks to hyperbolic space via their Laplacian. Sci. Rep. 6, 30108; doi: 10.1038/srep30108 (2016).
Warteschlangen
Rolf H. Möhring: Computerorientierte Mathematik I mit Java, Manuskript, TU Berlin, WS 2009/10, S. 102.
Juraj Hromkovič, Tobias Kohn: einfach Informatik – Programmieren, Klett, 2018.
Hyperbolische Geometrie
Marián Boguñá, Fragkiskos Papadopoulos & Dmitri Krioukov: Sustaining the Internet with hyperbolic mapping. Nature Communications, Vol. 162 (2010), S. 1-8.
Was die Welt im Innersten zusammenhält
Johann Wolfgang von Goethe: Faust: Eine Tragödie. 1808, Zitat von https://gutenberg.spiegel.de/buch/faust-eine-tragodie-3664/4
Aufruf am 18.09.2019
Lawrence C. Evans: Partial Differential Equations. American Mathematical Society, 2. Aufl. 2010, S. 21.
Hans Triebel: Höhere Analysis. Deutscher Verlag der Wissenschaften, Berlin, 1972, S. 599.
Zum Weiterlesen über Linearität:
Yuri I. Manin: Mathematik und Physik, Mathematik als Metapher Bd. 3, e-enterprise, 2017, S. 26-42.
Die Berliner Tunnelaufgabe
Mathe-Abiaufgaben 2019
https://www.tagesspiegel.de/downloads/24309422/1/abi-berlin.pdf
Simplon-Tunnel
https://upload.wikimedia.org/wikipedia/commons/4/4d/Simplon_Sudportal.jpg
Höhenprofil
https://upload.wikimedia.org/wikipedia/commons/a/a6/Simplontunnel.png
Aufrufe aller dieser am 17.08.2019
I. N. Bronstein, K.A. Semendjajew: Taschenbuch der Mathematik, Teubner, Stuttgart, Leipzig, Nauka, Moskau, 25. Aufl., 1991, S. 229 f.
Autobahnaufgabe
A. Bigalke, N. Köhler: Mathematik, Gymnasiale Oberstufe 11 in Brandenburg, Cornelsen, Berlin, 2019, S. 236
Doppelter Zufall
Kevin Hartnett: Random Surfaces Hide an Intricate Order, Quanta Magazine, vom 2. 07.2019,
https://www.quantamagazine.org/random-surfaces-hide-an-intricate-order-20190702/, Aufruf am 19.08.2019
Joachim Wedekind: Codierte Kunst, Tübingen, 2018, S. 171
Diskrete Faltung
https://en.wikipedia.org/wiki/Kernel_(image_processing), Aufruf am 04.08.2019
Faltung in Adobe Photoshop: http://ian-albert.com/old/custom_filters/, Aufruf am 04.08.2019
Fermat-Zahlen
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 2, 7, 579.
Die Primfaktorzerlegung erfolgte mit https://www.mathepower.com/primfaktor.php, Aufruf am 15.07.2019.
Für die größte bekannte Fermat-Primzahl siehe https://en.wikipedia.org/wiki/Fermat_number#Factorization_of_Fermat_numbers, Aufruf am 02.08.2019
Pépin-Test: https://en.wikipedia.org/wiki/P%C3%A9pin%27s_test, Aufruf am 10.08.2019.
Rekonstruktion von Bildern
Niloy Mitra, Iasonas Kokkinos, Paul Guerrero, Vladimir Kim, Kostas Rematas, Tobias Ritschel: Deep Learning for Graphics and Geometry Processing, Part 4: Supervised Applications, Vortrag auf der Eurographics 2018. http://geometry.cs.ucl.ac.uk/dl_for_CG/, Aufruf am 30.06.2019
David Eigen, Rob Fergus: Predicting Depth, Surface Normalsand Semantic Labels with a Common Multi-Scale Convolutional Architecture, ICCV 2015.
Zufallszahlen und CG
Idee nach: Donald Knuth: The Art of Computer Programming, Seminumerical Algorithms, Vol. 2, Addison Wesley Longman, 1997, S. 2
Zufallszahlen
Donald Knuth: The Art of Computer Programming, Seminumerical Algorithms, Vol. 2, Addison Wesley Longman, 1997, S. 10-17.
Zufallszahlentest
Heuristische Zufallszahlen, ebda. ÜA S. 6-7
Kritik an der Kongruenz-Methode:
https://de.wikipedia.org/wiki/Kongruenzgenerator#M%C3%A4ngel_der_erzeugten_Zahlen
https://de.wikipedia.org/wiki/Mersenne-Twister
Aufruf am 08.06.2019
Primzahlen
https://de.wikibooks.org/wiki/Primzahlen:_Tabelle_der_Primzahlen_(2_-_100.000)
Aufruf am 08.06.2019
TigerJython
www.tigerjython.ch, Aufruf am 25.04.2019
Liste aller Befehle: http://www.tigerjython.ch/index.php?inhalt_links=navigation.inc.php&inhalt_mitte=turtle/turtledoc.html, Aufruf am 17.06.2019
Juraj Hromkovič, Tobias Kohn: einfach Informatik – Programmieren, Klett, 2018.
Datenbanken: Ebda., S. 117.
Volkslauf-Beispiel: Ebda. S. 120
Neuronale Netze
Kevin Hartnett: Foundations Built for a General Theory of Neural Networks. Qunata Magazin, 31. 01. 2019, https://www.quantamagazine.org/foundations-built-for-a-general-theory-of-neural-networks-20190131/. Aufruf am 17.04.2019.
David Rolnick, Max Tegmark: The power of deeper networks for expressing natural functions, 2018, https://arxiv.org/pdf/1705.05502. Aufruf am 17.04.2019.
Henry W. Lin, Max Tegmark, and David Rolnick: Why does deep and cheap learning work so well? 2017, https://arxiv.org/pdf/1608.08225v4, Aufruf am 08.05.2019.
Satz von Bayes: https://de.wikipedia.org/wiki/Satz_von_Bayes, Aufruf am 08.05.2019.
Weierstrass' Approximationssatz: https://en.wikipedia.org/wiki/Stone%E2%80%93Weierstrass_theorem, Aufruf am 08.05.2019.
Bubble Sort Party
Donald Knuth: The Art of Computer Programming, Sorting and Searching, Addison-Wesley, 1998, S. 105 ff.
Der Zauberlehrling
Das Gedicht stammt von Goethe. Hier die Originalversion: https://de.wikisource.org/wiki/Der_Zauberlehrling_(1798), Aufruf am 14.04.2019.
Für die Abbildung des Goethe-Denkmals im Titelbild benutzte Oliver Hinzmann das Bild von © Bwag/Wikimedia auf https://de.wikipedia.org/wiki/Liste_der_Goethedenkm%C3%A4ler#/media/File:Wien_-_Goethedenkmal_(2).JPG als Vorlage.
Markus Gabriel: Schlauer als jeder Mensch? FAZ, 21.05.2018
https://www.faz.net/aktuell/wirtschaft/kuenstliche-intelligenz/kuenstliche-intelligenz-schlauer-als-jeder-mensch-15598222.html?premium, Aufruf am 20.03.2019.
Shannon-Formel für Buchstaben bei "Effi Briest"
Textvorlagen
Theodor Fontane: Effi Briest, Berlin, 1896. http://www.gutenberg.org/ebooks/5323, Aufruf am 2.3.2017
Alex Eskin, Maryam Mirzakhani: Invariant and stationary measures for the SL(2,R) action on Moduli space, https://arxiv.org/pdf/1302.3320.pdf, Aufruf am 31.03.2019.
Ludwig Wittgenstein: Tractatus logico-philosophicus, http://tractatus-online.appspot.com/Tractatus/jonathan/D.html, Aufruf am 31.03.2019.
Die Kunst des Programmierens
Donald Knuth: The Art of Computer Programming, Vol. 1, Addison Wesley Longman, 1997. S. 2 ff.
Maschinelles Lernen
https://www.nature.com/articles/s42256-018-0002-3.pdf, 05.03.2019.
Mathematische Gitter und Restklassen
Akshay Venkatesh: What Information Might the Topology of Locally Symmetric Spaces Contain? 2018. https://www.ias.edu/ideas/venkatesh-locally-symmetric-spaces (Aufruf am 26.02.2019)
Smith-Diagramm
https://de.wikipedia.org/wiki/Komplexe_Wechselstromrechnung
https://de.wikipedia.org/wiki/Leistungsanpassung
18.02.2019
Mathematisches Billard
Nach:
Marco Bettinaglio, Ferdinando Lehmann: Mathematisches Billard. Zwei Vorschläge zu projektartigem Unterricht, ETH Zürich, 1997, online hier.
Beim gleichseitigen Dreieck ist ihnen ein kleiner Fehler unterlaufen, sie schreiben
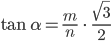
statt
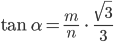
Komplexe Früchte
Hans Triebel: Analysis und mathematische Physik, Leipzig, 1981, S. 154 f.
Möbiustransformation
Das Beispiel stammt aus:
http://www2.math.uni-wuppertal.de/~fritzsch/lectures/geo/ge_k4b.pdf
Allgemeine Theorie komplexer Funktionen:
I. I. Priwalow: Einführung in die Theorie komplexer Veränderlicher, Moskau, 1983 (in Ru). S. 108 ff.
P. Günther, K. Beyer, S. Gottwald, V. Wünsch: Grundkurs Analysis, 1974, Teubner, S. 157 ff.
Retardierte Dgln
Alfred Döblin: Berlin Alexanderplatz. Die Geschichte vom Franz Biberkopf, Deutscher Taschenbuchverlag München, 48. Aufl. 2009, S. 99-100
Stefan Kretzmar, Nils Weber: Hölleluja!: Warum Handball der absolute Wahnsinn ist, Edel Books, Hamburg, 2018.
https://de.wikipedia.org/wiki/Retardierte_Differentialgleichung, Aufruf am 07.01.2019
Die Headerbilder dazu benutzen ein Foto von Alexander auf http://galerie.designnation.de/bild/44063, Aufruf am 07.01.2019.
Permutationen
Nach Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 189-190.
Logarithmische Kosmetikwerbung
Séduction #3/2018, Beilage der Süddeutschen Zeitung vom 17.11.2018
Quellen für weitere Preise
Valmont, Augenpflege
https://www.mehr-kosmetik-shop.de/valmont/pflege-augenringe.traenensaecke/
Hublot Big bang one click
https://www.hublot.com/de/kollektion/big-bang/big-bang-one-click-pink-sapphire-diamonds-39mm
Shalimar Guerlain
https://www.douglas.de/productbrand_091700.html?trac=+de.07x.guerlain..listing.cc.000009
Korrigan, lubin
https://www.meinduft.de/lubin-korrigan.html?gclid=EAIaIQobChMIpaqpsuGQ3wIVB-d3Ch30mAIjEAYYAiABEgKjvfD_BwE
Castaña Cloon Keen Atelier (2011)
https://www.jangeorge.com/products/cloon-keen-eau-de-parfums?variant=12442658734177
Dior J'adore
https://www.douglas.de/D%25C3%25BCfte-Damend%25C3%25BCfte-D%25C3%25BCfte-DIOR-J%E2%80%99adore_product_019720.html
Aufruf aller dieser am 09.12.2018
Bruttoinlandsprodukt
https://de.wikipedia.org/wiki/Liste_der_L%C3%A4nder_nach_Bruttoinlandsprodukt_pro_Kopf
Aufruf am 15.12.2018
Kamera-Charakteristik
Orhan Pamuk: Balkon, Steidl, 2018.
Jochem Berlemann: Audiovisuelle Produktion, e-enterprise, 2014, S. 123.
Marlene Schnelle-Schneyder: Sehen und Photographieren – Von der Ästhetik zum Bild, Springer, 2003, S. 138.
Weiterführende Literatur zum Zonensystem
Anselm Adam: The Negative, Little, Brown and Company, 13. Aufl. 2007.
Chris Johnson: The Practical Zone System for Film and Digital Photography, Focal Press, 4. Aufl. 2007.
Phil Davis: Beyond the Zone System, Focal Press, 4. Aufl. , 1999.
Detlef Möllering, Peter C. Slansky: Handbuch der professionellen Videoaufnahme, edition Filmwerkstatt, 1993.
Graphische Liebe
Die Euler-Charakteristik steht auf:
https://en.wikipedia.org/wiki/Euler_characteristic, Aufruf am 17.11.2018.
Mersenne-Zahlen
https://de.wikipedia.org/wiki/Mersenne-Zahl
https://www.mersenne.org/ Aufruf von beiden am 09.11.2018
https://www.mersenne.org/primes/?press=M82589933, Aufruf am 26.12.2018.
Evelyn Lamb: The Largest Known Prime Number. In: Mircea Pitici (Hrsg.) The Best Writing on Mathematics 2017, Princeton University Press, Princeton, Oxford, S. 7-9.
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 3.
Kachujin ... lineare Überlagerung von Gesichtern
Kim Hyeongwoo, Pablo Garrido, Ayush Tewari, Weipeng Xu, Justus Thies, et al.: Deep Video Portraits, ACM Trans. Graph., Vol. 37, No. 4, Article 163. Publication date: August 2018, arXiv:1805.11714v1 und Christian Theobalt: Vortrag auf der FMX 2018, Stuttgart am 27.4.2018.
3D-Models: maximo.com, 04.11.2018
3D-Rekonstruktion
Siehe auch, insbesondere fürs Bewegtbild:
Michael Zollhöfer, Patrick Stotko, Andreas Görlitz, Christian Theobalt, Matthias Nießner, Reinhard Klein, Andreas Kolb: State of the Art on 3D Reconstruction with RGB-D Cameras. In: K. Hildebrandt and C. Theobalt (Guest Editors): EUROGRAPHICS 2018, Volume 37 (2018), Number 2, STAR – State of The Art Report.
Christian Theobalt: Capturing and Editing Models of the Real World in Motion, Vortrag auf der FMX 2018, Stuttgart am 27.4.2018.
Ramanujan-Test
Die Anekdote steht auf https://en.wikipedia.org/wiki/Srinivasa_Ramanujan, Aufruf am 19.10.2018.
Schopenhauer
Arthur Schopenhauer: Die Welt als Wille und Vorstellung, Brockhaus, Leipzig, 1844. S. 143 ff.
https://opacplus.bsb-muenchen.de/Vta2/bsb10927136/bsb:BV011177450?page=13, Aufruf am 06.10.2018.
Pythagoreische Tripel
https://de.wikipedia.org/wiki/Pythagoreisches_Tripel
Antrittsvorlesung von Prof. Peter Scholze: https://www.youtube.com/watch?v=NdgQQfQLtWw, Aufruf beider am 5.10.2018
Kunst und Mathematik
https://en.wikipedia.org/wiki/Reynolds_transport_theorem, Aufruf am 22.09.2018
Genie-Kurve
Lu Liu et al.: Hot Streakes in artistic, cultural, and scientific careers, Nature vol. 559, S. 396-399 (2018).
Männer-tötendes Gift
Titelbild: © Madboy74, Drosophila melanogaster, Creative Commons CC0 1.0, https://de.wikipedia.org/wiki/Drosophila_melanogaster
Toshiyuki Harumoto & Bruno Lemaitre: Male-killing toxin in a bacterial symbiont of Drosophila, Nature 557, S. 252-255 (2018).
Handball-Wurfübung
Die Übung (mit einem Tennisball) stammt aus:
www.blv-nachwuchs.ch/service/Ball06.pdf, S. 4, Aufruf am 15.08.2018.
Torsion
Ignaz Urban: Monographia Loasacearum, Abhandlungen der Kaiserlichen Leopoldinisch-Carolinischen Deutschen Akademie der Naturforscher, Bd. 76, Halle, 1900.
L. D. Landau, E. M. Lifschitz: Lehrbuch der theoretischen Physik, Bd. VII, Elastizitätstheorie, Berlin, 1975, S. 73 ff.
Blaualgen
A. P. Belov, J. D. Giles: Dynamical model of buoyant cyanobacteria, Hydrobiologia 349: S. 87–97, 1997.
Ziomara P. Gerdtzen, J. Cristian Salgado, Axel Osses, Juan A. Asenjo, Ivan Rapaport, Barbara A. Andrews: Modeling heterocyst pattern formation in cyanobacteria, BMC Bioinformatics 2009, 10 (Suppl 6):S16, https://bmcbioinformatics.biomedcentral.com/articles/10.1186/1471-2105-10-S6-S16, Aufruf am 01.08.2018
G. Sudhakar, B. Jyothi, V. Venkateswarlu: Impact of paper mill effluents on the distribution of Cyanobacteria in the river Godavari, India, Waste Management, Vol. 11, S. 263-269, 1991
Hyun-Seob Song, William R. Cannon, Alexander S. Beliaev, Allan Konopka: Mathematical Modeling of Microbial Community Dynamics: A Methodological Review, Processes 2014, 2, 711-752; doi: 10.3390/pr2040711
S.A. Kulasooriya, D.N. Magana-Arachchi: Nitrogen fixing cyanobacteria: their diversity, ecology and utilisation with special reference to rice cultivation, J. Natn. Sci. Foundation Sri Lanka 2016 44 (2): S. 111-128.
Hans W. Paerl, Valerie J. Paul: Climate change: Links to global expansion of harmful cyanobacteria, water research 46 (2012) S. 1349 - 1363, https://www.sciencedirect.com/science/article/pii/S0043135411004386, Aufruf am 01.08.2018
Über Blaualgen in populären Medien
https://www.mdr.de/brisant/badeseen-ostsee-kueste-blaualgen-gefahren-100.html,
https://www.sueddeutsche.de/politik/blaualgen-die-schattenseite-des-sommers-1.4075022
https://www.zdf.de/nachrichten/heute-19-uhr/blaualgen-vermehren-sich-rasant-100.html
Alle diese wurden am 01.08.2018 aufgerufen.
Wie Apfelsinen natürlich trianguliert werden
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 152ff.
https://de.wikipedia.org/wiki/Euler-Charakteristik, Aufruf am 21.07.2018
Wie der Hirschwurz-Haarstrang mathematisiert wird
Zum Hirschwurz siehe https://de.wikipedia.org/wiki/Hirschwurz-Haarstrang, Aufruf am 15.07.2018
Wie Polynomnäherungen Verwirrung stiften können
Masashi Soga, Kevin J. Gaston: Extinction of experience: evidence, consequences and challenges of loss of human-nature interactions, Front. Ecol. Environ. 14, S. 94-101 (2016)
S. R. Rintoul, et al: Choosing the future of Antarctica, Nature Vol. 558, S. 233-241, 14. Juni 2018
Arndt Brunner: https://www.arndt-bruenner.de/mathe/scripts/gleichungssysteme.htm, Aufruf am 07.07.2018.
Lösung eines linearen Gleichungssystems: http://wims.unice.fr/wims/, Aufruf am 07.07.2018
Wie Natur, Kunst und Mathematik zusammenhängen
Bildungsgesetz der goldenen Spirale
https://en.wikipedia.org/wiki/Golden_spiral, Aufruf am 02.07.2018.
2. Ableitung bei Polarkoordinaten
I. N. Bronstein, K. A. Semendjajew: Taschenbuch der Mathematik, Teubner & Nauka, 1991, S. 283 f.
Raue Oberflächen
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 537 ff.
Andrea Weidlich (Weta Digital): Thinking in Layers - Material Modelling in a Modern Rendering Pipeline, Vortrag am 25.04.2018, FMX 2018, Stuttgart.
Dylan Sisson (Pixar): Latest Developments in Pixar's RenderMan, Vortrag am 25.04.2018, FMX 2018, Stuttgart.
https://en.wikipedia.org/wiki/Specular_highlight, Aufruf am 18.06. 2018.
Positionssysteme mit negativer Basis
Jerzy Dreszer: Mathematik-Handbuch für Technik und Naturwissenschaft, Leipzig, 1975, S.19 f.
Reelle Zahlen
Carl Friedrich Gauß: Carl Friedrich Gauss' Untersuchungen über höhere Arithmetik. Springer, Berlin, 1889, http://resolver.sub.uni-goettingen.de/purl?PPN373456743, Aufruf am 26.5.2018
E. Schwerdtfeger: Trainingsbuch Algebra, Verlag Europa-Lehrmittel, 2017, S. 84 f.
Ganze Zahlen
The Univalent Foundations Program: Quotients. In: Homotopy Type Theory, Institute for Advanced Study, 2013, S. 261 ff.
Eugen Schwerdtfeger: Trainingsbuch Algebra, Verlag Europa-Lehrmittel, 2017, S. 16.
Vollständige Induktion
Wolfgang Sartorius von Waltershausen: Gauss zum Gedächtniss. S. Hirzel, Leipzig, 1856, S. 12–13.
Linus Kramer: Was ist Mathe? In: Sira Busch: Was ist Mathe? http://summa.stiftungrechnen.de/was-ist-mathe/, Aufruf am 13.5.2018.
Gaußsche Summenformel: https://de.wikipedia.org/wiki/Gau%C3%9Fsche_Summenformel, Aufruf am 13.5.2018.
Rudolf vom Hofe, Bernhard Humpert, Heinz Griesel, Helmut Postel: Mathematik heute 9. Mittelschule/Oberschule Sachsen Hauptschulbildungsgang, Bildungshaus Schulbildungsverlage, Braunschweig, 2016, S. 182.
Terme und Umformungen
The Univalent Foundations Program: The natural numbers. In: Homotopy Type Theory, Institute for Advanced Study, 2013, S. 49.
Yuri Manin: Gödels Theorem. In: Mathematik als Metapher, e-enterprise, 2016, S. 237-272
Eugen Schwerdtfeger: Trainingsbuch Algebra, Verlag Europa-Lehrmittel, 2017, S. 7, 10, 11.
Feuerwehrfunktion
Christoph Berg, Julian Brüggemann, Bertold Heinrich et al.: Mathematik Technik – Fachoberschulreife, Cornelsen, Berlin, 2015, S. 56 f.
Gauß-Algorithmus
ebda. S. 22.
Dgln in der 10. Klasse
V. I. Arnold: Gewöhnliche Differentialgleichungen, Berlin, 1979, S. 23 f.
H. Griesel, H. Postel, R. v. Hofe: Mathematik heute 10, Regelschule Thüringen, Schroedel, 2014, S. 113.
Horizont als Zufallsweg
Kevin Hartnett: A Unified Theory of Randomness. In: Mircea Pitici (Hrsg.): The Best Writings in Mathematics 2017, Princeton University Press, Princeton und Oxford, S. 10-23.
Jason Miller, Scott Sheffield, Wendelin Werner: Non-simple SLE curves are not determined by their range. arxiv:1609.04799v3, 2018.
Steffen Rohde, Oded Schramm: Basic properties of SLE, arxiv:math/0106036v4, 2004.
Wiener Prozess: https://de.wikipedia.org/wiki/Wiener-Prozess, Aufruf am 31.03.2018.
Hausdorff-Dimension: https://de.wikipedia.org/wiki/Hausdorff-Dimension, Aufruf am 31.03.2018
Van der Corput-, Halton- und Hammersleyfolgen
https://en.wikipedia.org/wiki/Low-discrepancy_sequence , Aufruf am 25.05.2018.
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 443 ff.
Harald Niederreiter: Random Number Generation and Quasi-Monte Carlo Methods, SIAM, Philadelphia, 1992.
Hawkings schwarze Löcher
Nach: S. W. Hawking: Into a Black Hole, http://www.hawking.org.uk/into-a-black-hole.html, Aufruf am 21.3.2018
S. W. Hawking: Virtual Black Holes, https://arxiv.org/pdf/hep-th/9510029.pdf, Aufruf am 21.3.2018
Kontinuumshypothese I und II
Zum Weiterlesen für Teil I:
Yuri I. Manin: Georg Cantor und sein Erbe. In: Mathematik als Metapher, e-enterprise, 2016, S. 207-232.
Rationale und reelle Zahlen, rationaler Zahlenstrahl:
K. Erikson, D. Estep, C. Johnson: Angewandte Mathematik: Body and Soul, Vol. 1, Springer, Berlin, Heidelberg, 2004, S. 201-215.
Axiomensystem reeller Zahlen:
Vladimir A. Zorich: Analysis I, Springer, Berlin, Heidelberg, 2006, S. 38-82.
Paul Cohen: Wie ich »Forcing« entdeckte, e-enterprise, Lemgo, 2017, S. 126-128.
Übersetzung von:
Paul Cohen: The Discovery of Forcing, Rocky Mountain Journal of Mathematics, Vol. 32 (4), 2002, S. 1071-1100.
Im Zitat ist vermutlich gemeint:
Paul Cohen: Set Theory and the Cotinuum Hypothesis, New York, Benjamin, 1963.
Parakonsistente Logik
Alain Badiou, Gilles Haéri: Lob der Mathematik, Passagen Verlag, 2018, S. 60 f.
Alain Badiou: Logic of Worlds, Being and Event 2, continuum, 2009, S. 166 ff.
Bild an der Wand nach: Tamfang: H2checkers_2ii.png auf https://en.wikipedia.org/wiki/Triangle_group#/media/File:H2checkers_2ii.png, auf dem Tisch nach: Anton Sherwood: File:H2checkers 34i.png auf https://en.wikipedia.org/wiki/File:H2checkers_34i.png, alle beide am 03.03.2018 aufgerufen, sowie nach dem Muster vom letzten Beitrag von Tamfang, H2checkers_iii.
Mehrwertige Logik: Wie mehrwertige Logik Mathematik 4.0 einleitet In: Mathezartbitter 2015-2017, 25. Beitrag, e-enterprise, 2017.
Hyperbolische Parkettierung
Für das Poincare-Disk-Modell, siehe https://en.wikipedia.org/wiki/Poincar%C3%A9_disk_model
https://en.wikipedia.org/wiki/Uniform_tilings_in_hyperbolic_plane
Tamfang: H2checkers iii.png, siehe: https://commons.wikimedia.org/wiki/File:H2checkers_iii.png
Alle Aufrufe am 26.02.2018.
Wie Antonija die beste hyperbolische Idee hat. In: Mathezartbitter 2015-2017, 66. Beitrag, e-enterprise, 2017.
Bullet Time Setup
Bewegungsstudie nach https://whitelines.com/, Aufruf am 16.02.2018.
Tensoren
Lucien Hardy: On The Theory of Composition in Physics, arXiv:1303.1537v2, 2013.
Philip Ball: A World without cause and effect, Nature Vol. 546, S. 590-592, 29. 6. 2017.
Magdalena Zych, Fabio Costa, Igor Pikovski, Timothy C. Ralph, Caslav Brukner: General relativistic effects in quantum interference of photons, arXiv:1206.0965v2, 2012.
Michael Reed, Barry Simon: Methods of Modern Mathematical Physics, Academic Press, Rev. Edition, 1980, S. 49-53.
Yuri I. Manin: Mathematik und Physik, e-enterprise, 2017, S. 117-119.
Prozentrechnung
H. Athen, H. Griesel: Mathematik heute 7 für Gymnasien in Baden-Württemberg, Schroedel, Hannover, 1979, S. 7, 12.
Negativer Index of Refraction
Fresnelsche Formeln
https://en.wikipedia.org/wiki/Fresnel_equations, Aufruf am 18.1.2018
IOR
https://en.wikipedia.org/wiki/List_of_refractive_indices, Aufruf am 18.1.2018
Circe of Confusion
Nach: The Thin Lens Model and Depth of Fields. In: Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 368-375.
Für weitere Infos zum DoF siehe:
Jochem Berlemann: Audiovisuelle Produktion. 2. Aufl., e-enterprise, 2014.
Dunkirk-Zeittransformationen
Nolan-Interview:
Christopher Nolan explains the 'audio illusion' that created the unique music in 'Dunkirk', http://www.businessinsider.de/dunkirk-music-christopher-nolan-hans-zimmer-2017-7?r=UK&IR=T, Aufruf am 1.1.2017.
Topologische Begriffe:
Michael Reed, Barry Simon: Methods of Modern Mathematical Physics, Academic Press, Rev. Edition, 1980.
Dunkirk-Struktur
Filminfos, Bilder:
https://www.rottentomatoes.com/m/dunkirk_2017/#&gid=1&pid=n-1764181
https://www.warnerbros.com/dunkirk
http://www.dunkirkmovie.com/
Aufruf am 17.12.2017.
Joshua Levine: Dunkirk, The History Behind the Major Motion Picture, William Collins, 2017.
Nolan-Interview:
https://www.dga.org/Craft/DGAQ/All-Articles/1703-Summer-2017/WWII-Dunkirk.aspx,
Aufruf am 17.12.2017.
Infos zur Geschichte der Evakuierung:
https://de.wikipedia.org/wiki/Dunkirk_(2017)
https://en.wikipedia.org/wiki/Dunkirk_(2017_film)
https://de.wikipedia.org/wiki/Operation_Dynamo
Churchills Rede:
https://www.youtube.com/watch?v=1Okt_YrKPdw
https://www.winstonchurchill.org/resources/speeches/1940-the-finest-hour/we-shall-fight-on-the-beaches/
Aufruf aller dieser am 28.12.2017.
Kameramodelle
Matt Pharr, Wenzel Jakob, Greg Humphreys: Physically Based Rendering, 3. Aufl., Morgan Kaufmann Publishers, 2017, S. 82, 355ff., 378.
Rendergleichung
Das mathematische Modell stammt aus: A. A. Penzov, I. T. Dimov, L. Szirmay-Kalos, V. N. Koylazov: Analysis of the Monte Carlo Image Creation by Uniform Separation. In: I. Lirkov, S. Margenov, and J. Wa´sniewski (Hsgb.): LSSC 2009, LNCS 5910, S. 419–426, 2010, Springer-Verlag Berlin Heidelberg 2010.
James T. Kajiya: The Rendering Equation. Siggraph 1986, ACM 0-89791-196-2/86/008/0143
Reelle Zahlen
https://en.wikipedia.org/wiki/Real_number, Aufruf am 4.11.2017
Bertram Huppert, Wolfgang Willems: Lineare Algebra, Vieweg, 2010, S. 2.
Vladimir A. Zorich: Analysis I, Springer, 2006, S. 38ff.
Jean Dieudonné: Grundzüge der modernen Analysis, Vieweg, 1985, S. 29 ff.
Linkin Park: Crawling, Musik/Text: Chester Bennington, Rob Bourdon, Brad Delson, Joseph Hahn, Mike Shinoda. In: Hybrid Theory, Warner Bros. Records Inc. , 2000.