Finja, Fabian, Justin, Charly und Max sitzen in Italien fest. Sie müssen noch ein bisschen ausharren, kein Busunternehmen will sie nach Hause fahren. Aber das macht nichts. Sie freuen sich über die Berge, fahren ein bisschen Ski, messen Temperaturen, untersuchen den Hintereisferner und diskutieren das Open Global Glacier Model (OGGM) mit der partiellen DGL
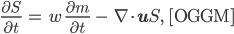
wobei
S ... Querschnittsfläche durch den Gletscher mit Parabelform,
w … Breite des Gletschers
u … Vektor für die Geschwindigkeit, mit der sich das Eis bewegt oder Wasser wegfließt
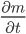 … Masseänderung
… Masseänderung
sind. Sie wollten diese Gleichung entlang eines Weges 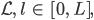 vom Gletschergipfel bis zum Fuß beschreiben, jeden Querschnitt, Stück für Stück. Inzwischen haben Justin und Charly sich im Internet über diese Gleichung informiert und festgestellt, dass dies die sogenannte Transportgleichung ist, hier ist es eine lineare. Sie sieht einfach aus, sie beschreibt den Transport von Flüssigkeiten mit bekannten Geschwindigkeiten u. Diese Gleichung ist immer noch eine große mathematische Herausforderung. Im nichtlinearen Fall heißt sie Navier-Stokes-Gleichung und zählt zu den Millenium-Problemen der Mathematik.
vom Gletschergipfel bis zum Fuß beschreiben, jeden Querschnitt, Stück für Stück. Inzwischen haben Justin und Charly sich im Internet über diese Gleichung informiert und festgestellt, dass dies die sogenannte Transportgleichung ist, hier ist es eine lineare. Sie sieht einfach aus, sie beschreibt den Transport von Flüssigkeiten mit bekannten Geschwindigkeiten u. Diese Gleichung ist immer noch eine große mathematische Herausforderung. Im nichtlinearen Fall heißt sie Navier-Stokes-Gleichung und zählt zu den Millenium-Problemen der Mathematik.
Schwache Gletscherlösungen
Charly Meist findet man für diese Probleme nur schwache Lösungen, also solche, die nicht unbedingt differenzierbar sind, sondern nur mit Testfunktionen aus geeigneten Räumen funktionieren …
Justin Ich verstehe gar nichts.
Charly Wenn wir mal unsere OGGM-DGL nehmen:
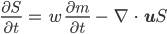
und alle Teile auf eine Seite der Gleichung bringen:
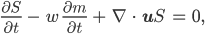
dann haben die beiden Gleichungen dieselben Lösungen. Wenn wir jetzt die Gleichung mit einer Funktion φ multiplizieren, die vielleicht an einer Stelle 0 ist, dann hat die neue Gleichung mehr Lösungen S:
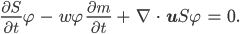
Jetzt benutzen wir noch den Trick: wir integrieren über ein Zeitintervall [0, T] und über die ganze Strecke  des Gletschers.
des Gletschers.
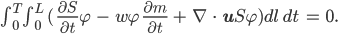
Justin Aha! Und was hat man davon?
Partielle Integration
Charly Man benutzt so eine Art partielle Integration, die kommt aus der Produktableitung zweier Funktionen:
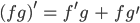
Justin Das kenne ich!
Charly Das stellen wir geschickt um:
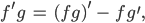
integrieren es und erhalten:
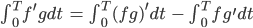
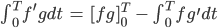
Wir fordern, dass eine der Funktionen f oder g am Rand 0 wird, nehmen wir mal g:
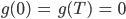
Dann geht es weiter, der mittlere Teil entfällt und:
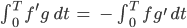
Definition schwacher Gletscherlösungen
Jetzt hat man die Aufgabe, f abzuleiten, auf die Aufgabe, g abzuleiten „abgewälzt“. Nur das Vorzeichen ändert sich bei den Teilen mit Ableitung – oder bei den Teilen ohne Ableitung. Wenn f an manchen Stellen nicht differenzierbar ist, dann ist das nicht schlimm, solange g differenzierbar ist, das Integral lässt solche Unstetigkeiten „verschwinden“. Auf diese Weise findet man mehr Lösungen der DGL – sogenannte schwache – und hofft, dass unter diesen Lösungen eine geeignete stetige und differenzierbare ist.
Bei uns wäre S eine schwache Lösung des OGGM, wenn für alle geeigneten Testfunktionen φ
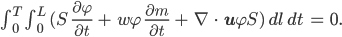
und den Bedingungen
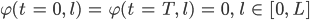
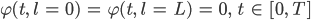
ist. Das mal so ganz grob. Dazu gehören noch Räume und die Randbedingungen wären auch noch anzupassen, aber verstehst du ungefähr das Prinzip?
Justin Ja, ich glaub‘ schon.
Charly Das ist eine bekannte Theorie von 1989 von Pierre-Louis Lions und Ronald DiPerna. Außerdem ist es möglich, dass es gar keine oder nur schwache Lösungen des OGGM für den Hintereisferner gibt.
Justin Wie kann ich mir denn schwache Lösungen vorstellen? Gibt es da mal ein Beispiel?
Konstruktion des Beispiels der linearen Transportgleichung
Charly Ja, schau mal hier, ich habe was gefunden: Nehmen wir mal die Gleichung
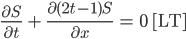
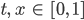
Justin Hmm, ein Teil unserer partiellen DGL fällt weg?
Charly Ja, der Teil mit der Masseänderung.
Justin Na, gut.
Charly Für diese Gleichung sind 2 verschiedene Lösungen bekannt:
1. Lösung
Die 1. Lösung ist die:
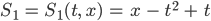
Justin Hmm?
Charly Lass uns die mal zeichnen. Wir überlegen mal, wie sie am Rand des Definitionsgebietes aussieht.
Justin Klar, mache ich, für
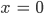
haben wir
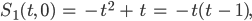
das ist eine Parabel mit Nullstellen in 0 und 1, für

haben wir
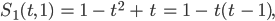
das ist dieselbe Parabel, nur um 1 nach oben verschoben.
Für
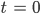
wird aus der Formel für S1:
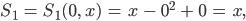
das ist ein linearer Anstieg und für
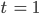
kriegen wir dasselbe raus:
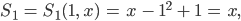
mit einem Grafikprogramm kann ich das zeichnen:
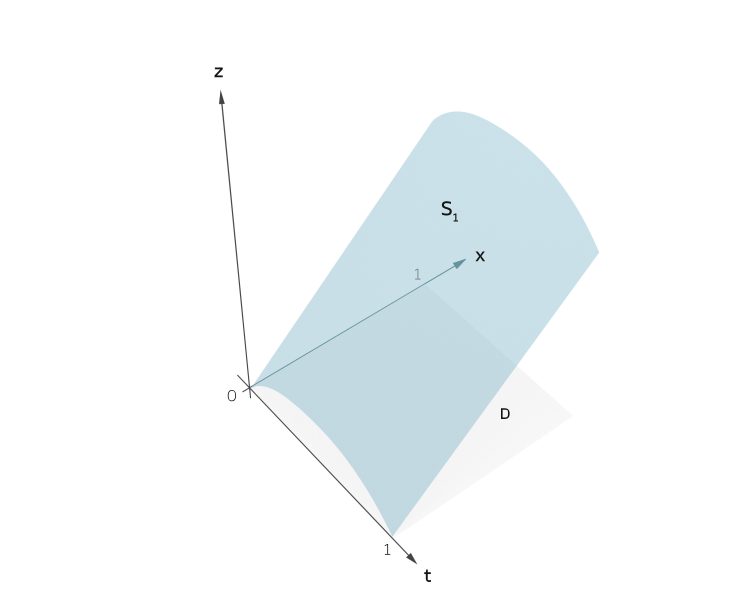
Justin Okay, die Fläche ist aber differenzierbar!
2. Lösung
Charly Ja, richtig. Es geht noch weiter. Für ein kleines Stück des Definitionsbereiches
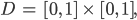
nämlich da, wo
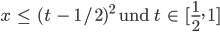
ist, da gibt es eine 2. Lösung:
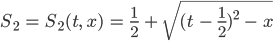
Justin Verstehe, man kann die Wurzel nur ziehen, wenn
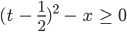
Charly Stimmt. Lass uns mal den Weg 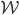
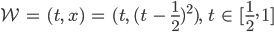
betrachten. Er teilt den Definitionsbereich D in 2 Teile: D1 und D2. Kannst du mal diese Fläche S2 mit einem Grafikprogramm zeichnen?
Justin Klar, hier!
Charly Und jetzt geht die Idee so, dass wir eine zusammengesetzte Lösung konstruieren, im Teil D1 nehmen wir S1,
in dem anderen die S2.
Justin Moment, ich zeichne das mal:
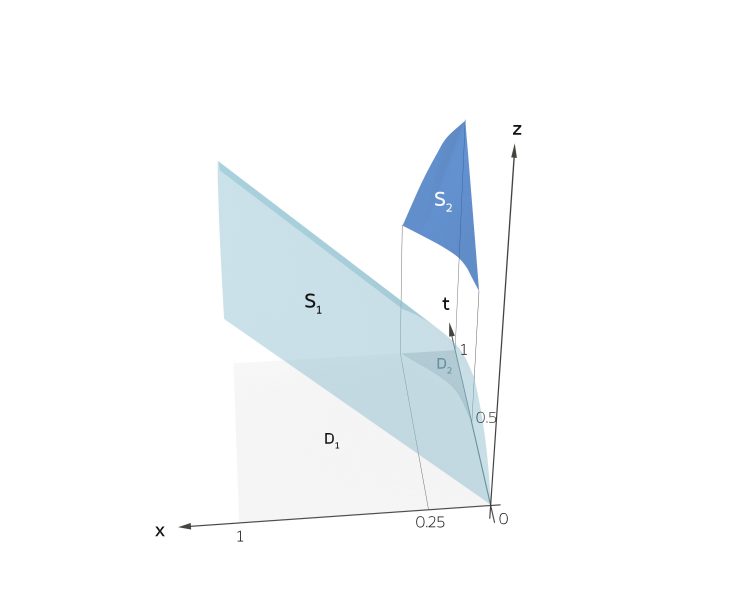
Charly Gut! Siehst du, dass genau über dem Weg 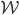 ein Sprung ist? Hier wäre die Lösung weder zeitlich noch räumlich stetig.
ein Sprung ist? Hier wäre die Lösung weder zeitlich noch räumlich stetig.
Justin Stimmt, da gibt es einen richtigen Sprung. Ist das trotzdem eine „schwache Lösung“ der DGL?
Charly Ja, ist es. Wenn das tatsächlich eine Gletscher-Querschnittsfläche wäre, dann wäre sie für manche Zeiten t und machen Punkte x nicht stetig. Das passt aber nicht zu unserer Anwendung. Das Schmelzen des Eises sollte differenzierbar in Zeit und Raum sein.
Justin Und nun? Gibt es keine „richtigen“ Lösungen, ist es hoffnungslos, die Gletscher zu berechnen? Aber die Geologen haben doch die Gletscher simuliert?! Wir müssen sie fragen, was sie eigentlich berechnet haben!
Charly Unsere Überlegungen und Deine Zeichnungen sind nicht umsonst. Wir verstehen das Problem jetzt besser und morgen fragen wir den Geologen.
Übungsaufgaben
- Teste ob, S1(t, x) und S2(t, x) Lösungen von [LT] sind!
- Ist
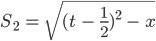
für
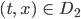 auch Lösung von [LT]?
auch Lösung von [LT]?
Lösung
2. Ja

Ein kleines Gedicht zur Mathematik:
MATHEFANS
Die Mathematik erfordert Wissen,
Dich nicht als ewiges Ruhekissen.
Für die mathematischen Prozesse
Braucht es Geist und Akkuratesse.
Sie lieben Summen und Differenzen
Genauso wie Wurzeln und Potenzen.
Vektorrechnung und Trigonometrie,
Wie auch die Algebra begeistern sie.
Differential, Integral - ganz egal,
Sie beherrschen Infinitesimal.
Sie quadrieren und interpolieren,
Wollen ständig mit Zahlen jonglieren.
Sie steh'n auf Euklid und Pythagoras,
Haben an Logarithmen großen Spaß.
Sie bearbeiten Funktionen versiert,
Die Kurvendiskussion wird geführt.
Extremwerte sind gar kein Problem,
Sie lösen jedes Gleichungssystem.
Sie führen die kniffligsten Beweise,
Berechnen flott Trapeze und Kreise.
Das alles ohne den geringsten Frust,
Mathematik ist ihnen eine Lust.
Rainer Kirmse , Altenburg
Mit freundlichen Grüßen