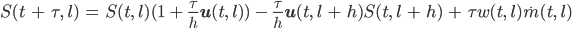Heute fahren Finja, Fabian, Justin, Charly und Max mit dem Wissenschaftler von der Uni zum Teufelsegg (3050 m). Ausnahmsweise dürfen sie heute mit dem Lift hochfahren, sie sind ja keine Touristen. Die schönste Hütte Südtirols ist leider geschlossen. Sie wollen die Wetterstation Teufelsegg am Hintereisferner besichtigen. Dort treffen sie den Spezialisten Matthias von der Uni.
Matthias Seid gegrüßt, ihr Buben und mein Mädel, wie ischts? Wir stehen grad hier auf 3000 m, wo die größte Schnee- und Eisfläche ist, hier ist ungefähr die Stelle, wo die Massenbilanz des Gletschers ihr Vorzeichen ändert. Das ist auch die Stelle, wo sich der Eisfluss im Vorzeichen ändert. Nach oben war bis jetzt immer ewiges Eis, nach unten ist es – natürlich im Jahresmittel – geschmolzen. Das muss man alles berücksichtigen, um die Dynamik am Kees zu simulieren.
Justin Guten Tag, Matthias. Wir haben gestern mit Charly die lineare Transportgleichung besprochen und herausgefunden, dass die sehr schwierig ist und – möglicherweise ist sie gar nicht lösbar. Wir verstehen nicht, was ihr an der Uni genau nähert, wenn es vielleicht gar nichts gibt, was zu nähern ist. Sie haben von ihren Simulationen erzählt, und jetzt wollen wir wissen, was sie genau an ihrer Uni simulieren.
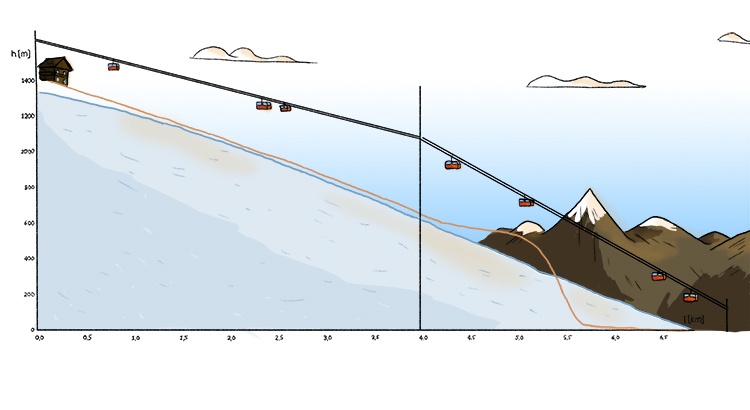
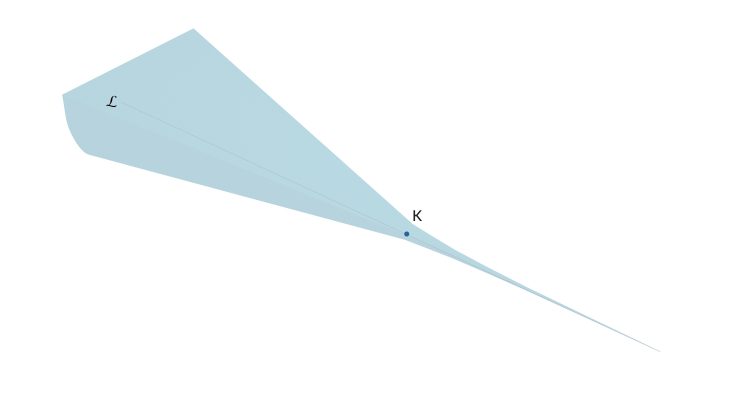
Matthias Leiwand! Iahr seid mir welche! Schaut mal hier, das ist der Hintereisferner. Er hat oben, oberhalb dieses kritischen Punktes K sehr viel Eis – und nach unten folgt die Zunge. Wir haben ein parabelförmiges Profil entlang des Wege 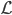 . Wenn wir den Weg etwas vereinfachen, dann kann ich euch unseren Algorithmus erklären, und ihr könnt den selbst prüfen und überlegen, wie gut er ist.
. Wenn wir den Weg etwas vereinfachen, dann kann ich euch unseren Algorithmus erklären, und ihr könnt den selbst prüfen und überlegen, wie gut er ist.

Justin Ja, gut, das machen wir.
Matthias Also, wir haben die DGL für unser Transportproblem am Kees:
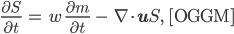
wobei
S ... Querschnittsfläche durch den Gletscher mit Parabelform,
w … Breite des Gletschers
u … Vektor für die Geschwindigkeit, mit der sich das Eis bewegt oder Wasser wegfließt
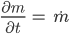 … Masseänderung
… Masseänderung
Jetzt nehmen wir den Weg 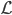 einfacher, also ohne Kurven und Ecken, ungefähr so:
einfacher, also ohne Kurven und Ecken, ungefähr so:
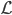 und kritischem Punkt K
und kritischem Punkt K
Justin Linear? Das ist eine starke Vereinfachung.
Matthias Du kannst ja dann die echte Kurve nehmen, haha.
Vorwärtsdifferenzen für die Zeit
Für die zeitliche Ableitung von S nehmen wir sogenannte Vorwärtsdifferenzen
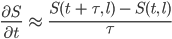
Fall u ≥ 0
Ist u ≥ 0, dann nehmen wir sogenannte rückwertige Differenzen für den Ort:
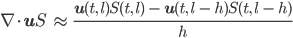
Das setzten wir in die DGL ein und erhalten die Differenzengleichung:
1. Differenzengleichung
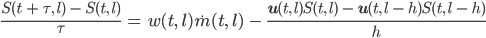
Daraus ergibt sich eine Rechenvorschrift, mit der man die Fläche zu einem nächsten Zeitpunkt t + τ:
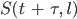
in Abhängigkeit von
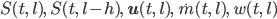
berechnen kann:
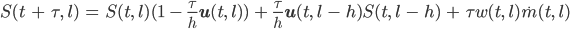
Courant-Friedrichs-Levy-Bedingung
Ist der Anfangswert
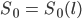
zur Zeit t = 0 gegeben und u, 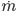 , w bekannt, dann kann man S(t, l) von l=0 bis zum Ende l=L berechnen, man muss nur überlegen, wie man die Enden l=0 und l=L behandelt, das nennt sich Randbedingung. Das Verfahren ist stabil für bestimmte Verhältnisse von τ und h, nämlich, wenn
, w bekannt, dann kann man S(t, l) von l=0 bis zum Ende l=L berechnen, man muss nur überlegen, wie man die Enden l=0 und l=L behandelt, das nennt sich Randbedingung. Das Verfahren ist stabil für bestimmte Verhältnisse von τ und h, nämlich, wenn
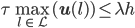
ist und
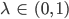 .
.
Justin Verstehe. Dann liegt der Faktor bei S(t, l) zwischen 0 und 1, so können die Werte für S nicht unbeschränkt wachsen.
Matthias Recht so!
Finja Wollen wir das mal berechen, sieht doch gar nicht so schwer aus!
Matthias Klar, habt ihr schon gesehen, dass unser Vektor u, der jetzt eine Zahl wird, oberhalb vom Teufelsegg u negativ wird, da fließt nichts ab!
Finja Na gut. Wir können es ja trotzdem probieren!
Matthias Du bischt ja fesch! Das läuft total aus dem Ruder! Das geht gar nicht. Für negative u muscht du eine andere Diskretisierung wählen.
Finja Aha, und wie geht die? Sollen wir dann das Gegenteil machen? u kommt nur im Ort vor, also Vorwärtsdifferenzen für die örtliche Ableitung?
Matthias Ei, Mann, du biascht gud! Jawoll, das machen wir.
Fall u ≤ 0
Ist u ≤ 0, nehmen wir Vorwärtsdifferenzen entlang des Weges:
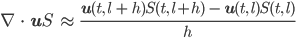
Dann erhalten wir als Differenzengleichung:
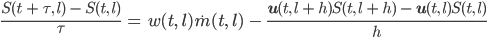
und können
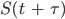
in (anderer) Abhängigkeit von
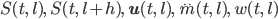
berechnen. Die Stabilitätsbedingung ist in diesem Fall
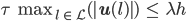
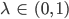
Finja Das war's schon?
Matthias Ja. Wir vereinfachen noch:
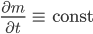
Dann bin ich ja mal gespannt.
Finjas und Justins Gletschersimulation
Finja Wollen wir mal?
Justin Gut. Was nehmen wir für die Weite w entlang des Weges 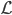 ?
?
Finja Vielleicht eine Exponentialverteilung?
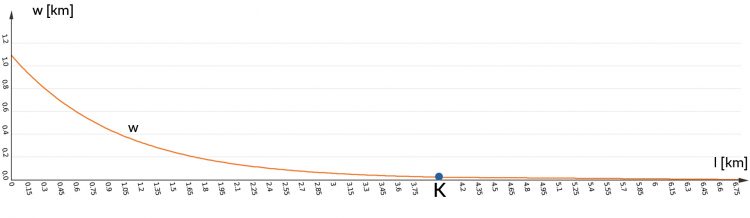
Sie nehmen dieselbe zeitliche Änderung der Masse wie beim letzten Mal. Für den Fluss müssen sie ein bisschen probieren, um mit Matthias mithalten zu können. Sie wählen schließlich einen Fluss u, der oberhalb vom kritischen Punkt K fast Null, aber positiv ist, doch weiter oben negativ ist – ab einem weiteren kritischen Punkt K', dort, wo die Sonne auf den Gletschergipfel knallt; unterhalb K ist u wieder negativ.
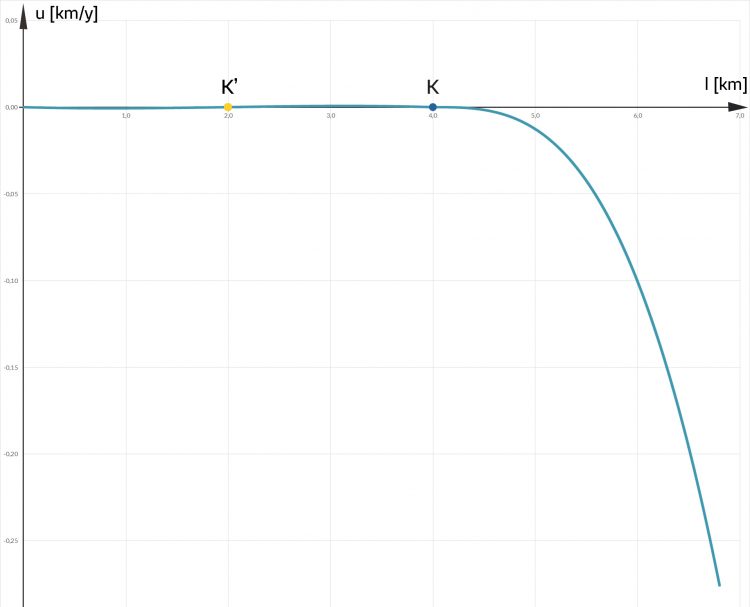
Daraus haben sie das Differenzenschema gelöst, in so vielen Teilschritten, dass es 5 Jahre wurden, haben wegen
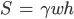
Die Höhe h = h(l) aus S berechnet und folgendes erhalten:
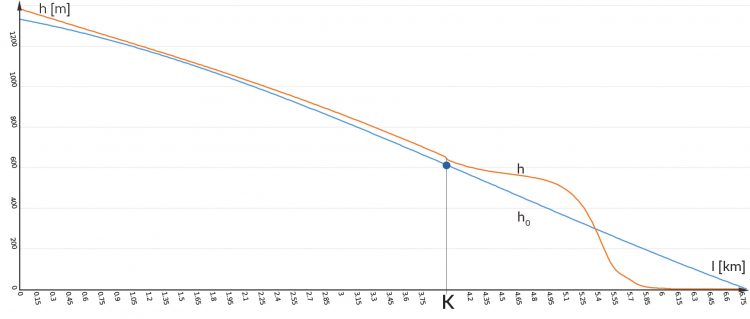
Matthias Mit eurem Setting habt ihr berechnet, dass sich die Zunge in 5 Jahren so schnell zurückgezogen hat wie bisher in 50 Jahren. Jo, mei!
***
Übungsaufgabe
Bestimme die Vorschrift zur Berechnung von S(t + τ, l) für u ≤ 0.
Lösung