Finja, Fabian, Justin, Charly und Max müssen jetzt nach Hause fahren. Die Kinder und Charly nach NRW, Max fährt nach Berlin. Zu Hause kommen sie in eine 14-tägige Quarantäne. Aber mit modernen Medien können sie sich austauschen.
Justin schreibt an alle Hallo! Wie geht es euch? Geht es irgendwie weiter mit unserem Gletscher-Projekt? Sollen wir hier Däumchen drehen?
Finja antwortet an alle Hallo zusammen! Ich habe zwar etwas Fieber und Husten, aber mir ist langweilig! Gestern, als ich so im Bett lag, habe ich mir unsere Rechnung noch mal angeschaut. Da ist mir aufgefallen, dass wir in unserem Eifer bei der Berechnung der Differenzengleichung die eigentliche Fragestellung vergessen haben. Was haben wir eigentlich ausgerechnet?
Differenzengleichung quo Differenzialgleichung
Justin Na, wir haben die Differenzengleichung für den Gletscher gelöst!
Finja Macht das Sinn?
Charly Hallo zusammen! Schön, dass ihr da seid. Ja, ein bisschen Sinn macht das schon. Immerhin konvergiert ja der Differenzenquotient zur Ableitung, wenn die Zeit- oder Ortsschrittweiten nach Null gehen.
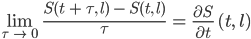
Aber du hast recht, Finja, das geht natürlich nur bei einer differenzierbaren Lösung. Toll, dass du das bemerkt hast. Martin Burger nimmt in seinem Skript zum Differenzenschema sogar eine zweimal differenzierbare Lösung für die Konvergenz der Differenzenlösung an diese.
Finja Aber wir wissen nicht, ob es eine zweimal differenzierbare Lösung gibt? Richtig? Meist gibt es nur schwache Lösungen?
Charly Stimmt! Es ist wirklich schwierig und anspruchsvoll.
Fabian Hallo! Ich bin auch dabei! Mir geht es gut. Ich verstehe nicht, dass bis jetzt kein Mathematiker diese Aufgabe gelöst hat. Keiner in Berlin, keiner in Bonn? Dabei ist das doch so wichtig! Wir wollen ausrechnen oder simulieren, wie lange die Gletscher noch da sind und wie sie sich verändern. Das ist wichtig für unseren Planeten und für unsere Zukunft! Wieso hat keiner Zeit dafür?
Stand der Forschung
Charly Justin, hallo, schön, dass es dir gut geht. Du bist ja ziemlich wütend. Vielleicht stehen die Werkzeuge noch nicht bereit? Beim Fermatproblem hat es 300 Jahre gebraucht.
Einige Mathematiker haben schon etwas in der Richtung gemacht. Pierre-Louis Lions und Ronald DiPerna haben Bedingungen für die Lösungen und Näherungen für Transportgleichungen im n-dimensionalen Raum gefunden. Das kann man eher für Gase, Winde und Auspüffe anwenden.
Fabian Aha! Was noch?
Charly Cédrik Villani und Clément Mouhot haben im n-dimensionalen Raum die Boltzmann-Gleichung untersucht. Die hat Anwendungen in der statistischen Physik und der kinetischen Gastheorie.
Fabian Aber warum haben die nicht die Gletscher untersucht?
Charly Die Boltzmann-Gleichung ist noch schwieriger und war für sie vermutlich reizvoller. Immerhin hat Villani dafür die Fields-Medaille bekommen.
Justin Und was machen die jungen Mathematiker?
Schwache Lösungen im beschränkten Gebiet
Charly Das Beispiel der schwachen, nicht differenzierbaren Lösung stammt von einem jungen Mathematiker, von Arne Roggensack. Warte mal, hier ist seine Dissertation. Er hat unsere Transportgleichung im beschränkten Gebiet untersucht und die Bedingungen für schwache Lösungen formuliert.
Finja Aha, und wie lauten die?
Charly Der Fluss u und die Anfangsbedingung müssen bestimmte sogenannte Regularitätsbedingungen erfüllen. Außerdem müssen die beschränkt sein. Doch vor allem sind die Randbedingungen an das Gebiet – das wäre unser Gletscher – entscheidend. Roggensack teilt die Ränder ein in die Teile mit eingehendem Fluss u- und die mit ausgehenden Fluss u+. Er fordert die Beschränktheit für den auf die Fläche S von außen eingehenden Fluss (Su-).
Finja Wie stelle ich mir das vor?
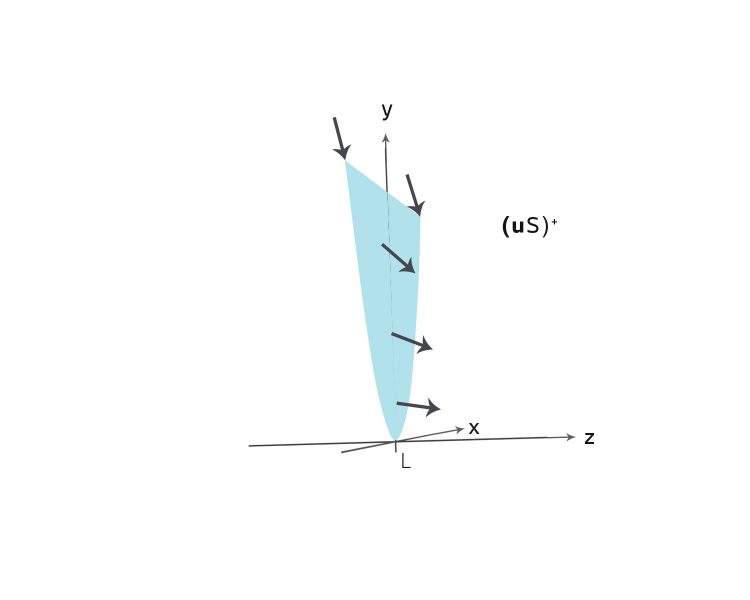
Charly Wenn wir das Modell mit dem parabelförmigen Querschnitt nehmen und die DGL für den Querschnittsfläche S haben, so:
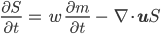
(der Gletscher ist von unten und von der Seite in den Berg eingebettet), dann brauchen wir nur noch die Information, was an den freien Rändern passiert.
Justin Okay! Verstehe! Wenn es schneit, kommt was dazu, wenn die Sonne scheint, schmilzt etwas. Wartet, ich zeichne das!
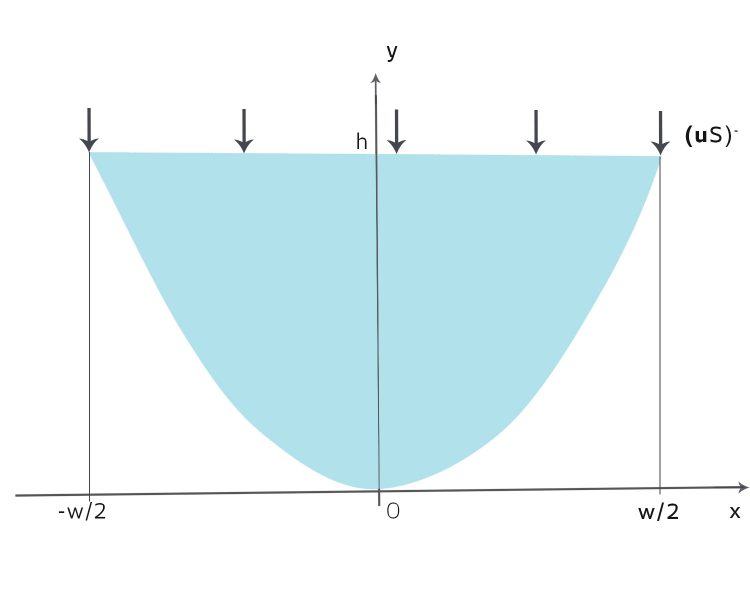
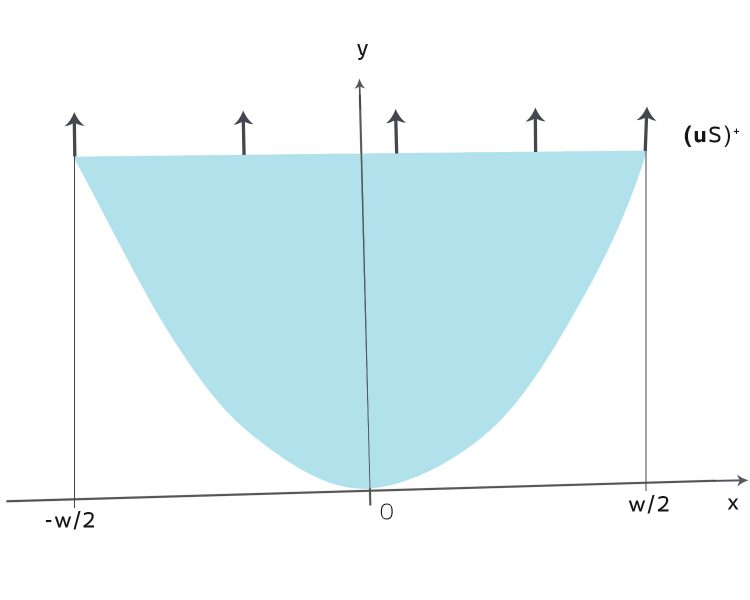
Justin Verstehe! Jetzt brauchen wir die Information, an welcher Stelle was passiert? Bis jetzt gibt es nur 2 Wetterstationen, eine an der Zunge und eine bei 3000 m Höhe. Das reicht nicht!
Ausblick
Finja Ist das nicht alles ganz hoffnungslos? Wir brauchen ganz viele Daten, um auszurechnen, wie sich der Gletscher ändert. Wir brauchen noch viel mehr Wetterstationen? Vielleicht haben die Mathematiker deshalb aufgegeben?
Max Hallo, Finja, Justin, Fabian und Charly! Ich bin gerade in Berlin angekommen. Unsere Berichte vom Hintereisferner sind gelesen worden. Ich soll euch danke sagen! Es ist gar nicht schwer, kleine Wetterstationen einzurichten, wir brauchen ja nur die Temperatur und den Niederschlag zu messen. Teuer ist es auch nicht. Ihr habt ja schon mal ein u mit 2 Vorzeichenwechseln genommen, das war doch genauso gut wie Matthias‘ Simulation!
Charly Hey! Max, grüß dich!
Justin Hey, Max, da mache ich mit! Wir kaufen ein paar Rasperry Pi und messen das Wetter! Super!
Finja Jetzt fehlt nur noch die mathematische Seite. Können wir nicht all die großen und all die jungen talentierten Mathematiker bitten, das Open Global Glacier Model zu lösen? Wir liefern die Daten, wir simulieren die Langzeitentwicklung, wenn wir wissen, dass das Modell für den Hintereisferner eine differenzierbare Lösung hat.
Max Hey Finja, gute Idee! Schreib doch mal einen offenen Brief, ich schaue mal, wo wir den veröffentlichen!
Finja Justin und Fabian, helft ihr mir?
Justin und Fabian Na klar!
***
Übungsaufgabe
Welche Situation bei den Randbedingungen fehlt noch?
Lösung
Wenn man davon ausgeht, dass der Gletscher oben an den Berg grenzt, bleibt noch das offene Ende an der Zunge einzubeziehen.