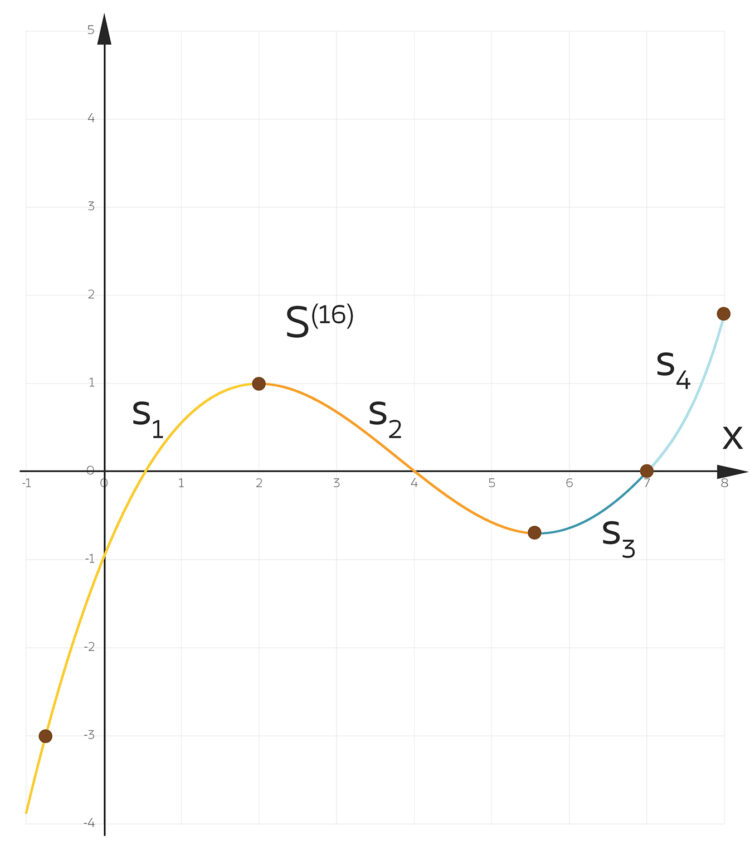
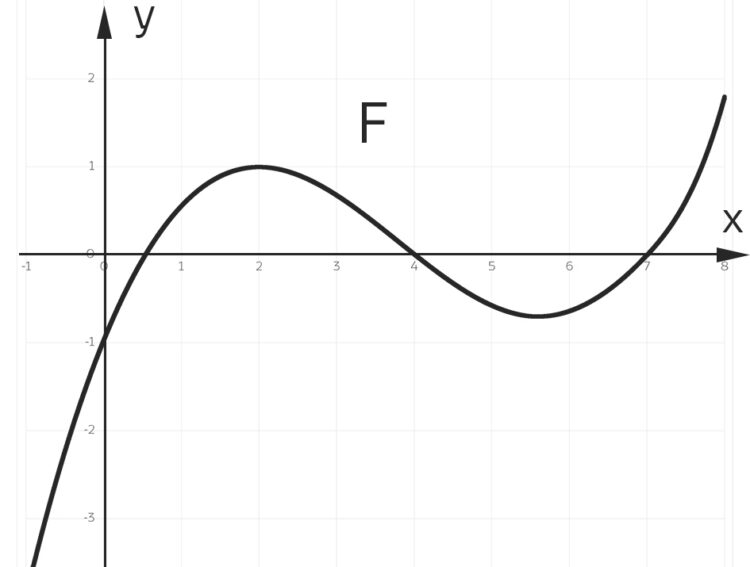
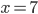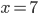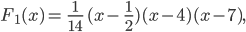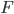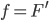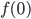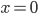Rike und Charly haben sich vorgenommen, als Alternative zur Trainingsstrecken-Aufgabe selbst eine übersichtliche und anwendungsnahe Abiaufgabe zu entwerfen. Geht das zum Thema Skilauf? Charly hat die Idee, kleinere Sprungschanzen, die manchmal zu Skiabfahrtpisten dazugehören, zu untersuchen. Vor allem die Landebahnen dazu sollen wie „richtige“ Skischanzen den gängigen Standards genügen. Er schlägt vor, dass die Schüler und Schülerinnen eine parameterabhängige Kurve p3(x) mit den folgenden Eigenschaften bestimmen:
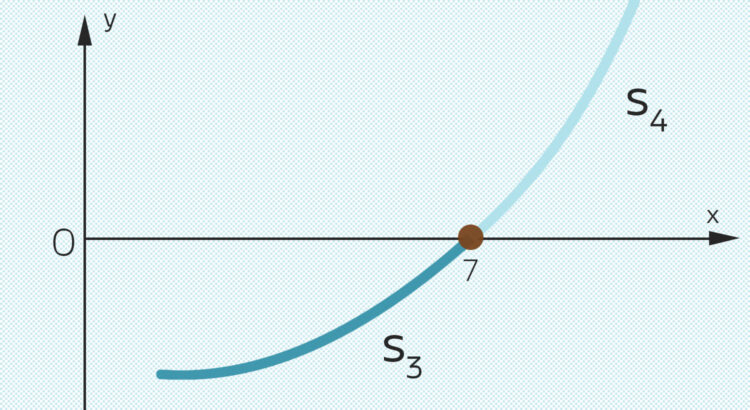
Eigenschaften der Landebahnkurve
Die Kurve p3(x) ist ein Polynom 3. Grades:
p3(x) = ax³ + bx² + cx + d.