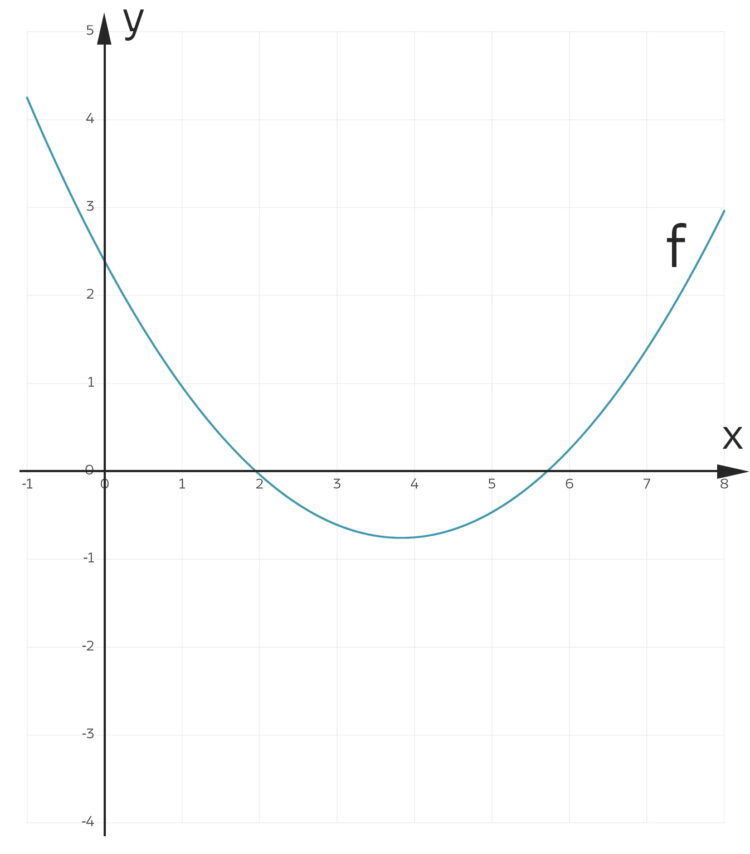
Als Rike vom Joggen wiederkommt, findet sie Charly ganz verzweifelt. Der Stundenplan fürs neue Schuljahr steht so gut wie fest und wie es aussieht, soll Charly neben Sport wieder einen Abikurs in Mathe übernehmen. So hat er sich weitere Abiaufgaben von Berlin-Brandenburg angeschaut, so auch die (hilfsmittelfreie) Analysis-Aufgabe für den Leistungskurs von 2021. In dieser Aufgabe geht es darum, aus einer Grafik für eine Stammfunktion  die zugehörige Funktion
die zugehörige Funktion
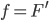
zu finden und deren Eigenschaften zu diskutieren.
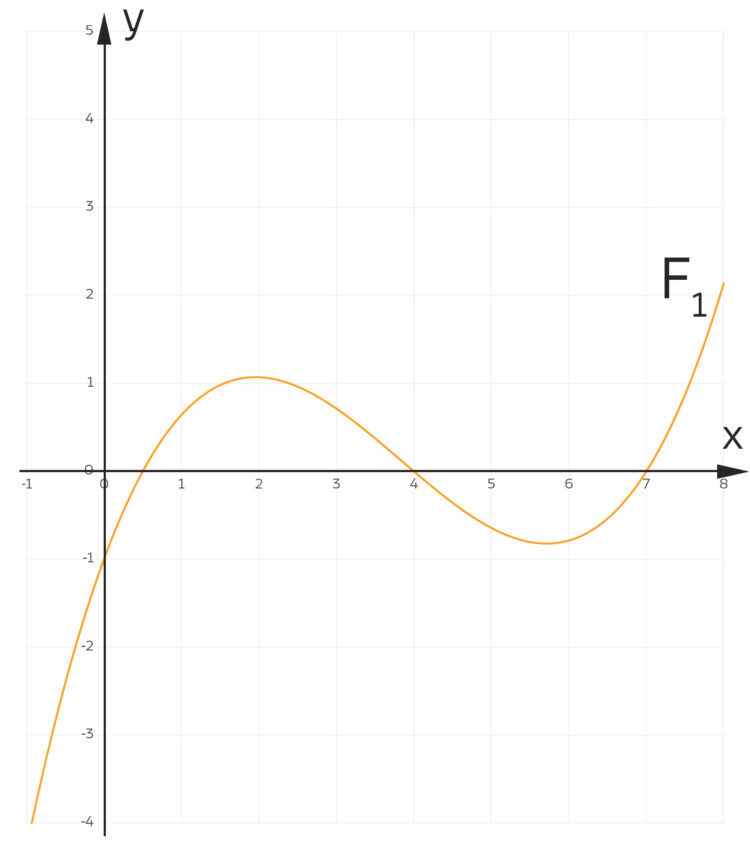
Die grafische Darstellung der Funktion F
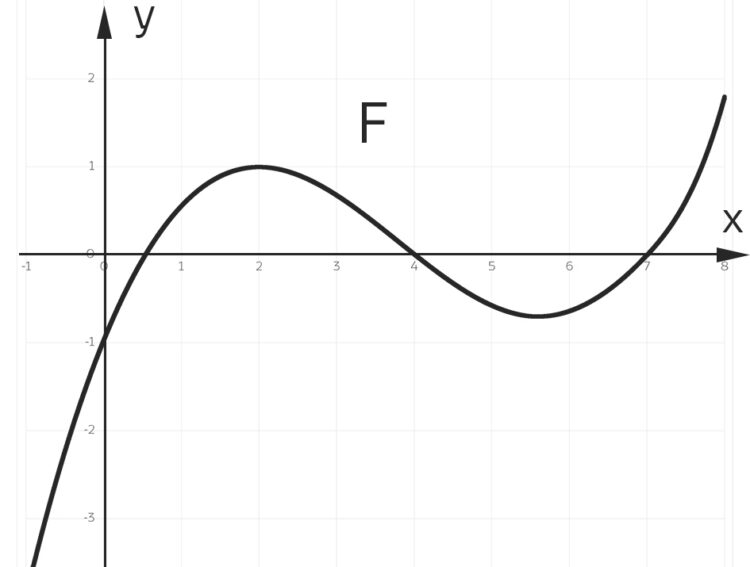
 . Abbildung nach [Ott, Schomburg, 2021]
. Abbildung nach [Ott, Schomburg, 2021]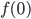 von
von  an der Stelle
an der Stelle 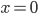 „näherungsweise“ bestimmt werden. Er zeigt Rike die Aufgabe.
„näherungsweise“ bestimmt werden. Er zeigt Rike die Aufgabe.
Charly Um den Anstieg von 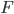 an der Stelle
an der Stelle 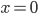 grafisch zu bestimmen, reicht die Genauigkeit der Zeichnung nicht aus.
grafisch zu bestimmen, reicht die Genauigkeit der Zeichnung nicht aus.
Rike So ca. 2???
Berechnungsmethoden, Hilfsmittel und Lernen
Charly Klar, so ca. 2. Um das genauer herauszufinden, müsste man die Zeichnung größtmöglich auf Millimeterpapier ausdrucken….
Rike … oder digital zur Verfügung stellen.
Charly Klar doch, Rike! Wie krass ist es denn, ein internetfähiges Tablet in der Abi-Klausur zu haben, wissenschaftliche Taschenrechner, Tabellenkalkulationsprogramme oder sogar Tools aus dem Internet zu benutzen!
Rike Auch ChatGPT?
Charly Auch ChatGPT! Ich denke, in der Schule sollte es nicht darum gehen, ein Ergebnis mit altbekannten Methoden in einer vorgesehenen Zeit und vor allem ohne Hilfsmittel zu erhalten! Vor allem in Mathe ist es mehr als altmodisch, nur mit den 4 Grundrechenarten angewandte Aufgaben zu lösen.
Rike Sondern?
Charly Na, ein mathematisches Problem zu lösen – mit allen möglichen und unmöglichen Methoden! Dabei klappt bestimmt nicht alles, manchmal verrennt man sich und kommt in eine Sackgasse. Doch solange man die Wege notieren und begründen kann, ist doch ein Erkenntnisgewinn da, das ist Lernen!
Rike Charly, warum bist Du denn so wütend! Ich glaube, Du hast gerade das Credo des Matheunterrichts 2.0 erfunden!
Charly Danke!
Rike Charly, was du da beschrieben hast, das Zulassen aller Methoden und das Verrennen in Sackgassen, ich glaube, das machen wir beide gerade.
Charly Ja, das machen wir beide. Doch es reicht nicht, wenn nur wir beide das machen.
Rike Stimmt, das reicht nicht. Los, jetzt lass uns in die nächste Sackgasse rennen.
Charly Okay.
Charlys Polynom-Ansatz
Rike Deine Kurve sieht aus wie ein Polynom 3. Grades, die Nullstellen liegen bei
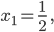
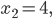
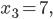
richtig?
Charly Ja, genau. Mit den Infos mache ich den erwarteten Ansatz 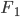 für die Stammfunktion
für die Stammfunktion 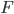 :
:
 . Diese Konstante
. Diese Konstante  bekomme ich durch einen Funktionswert, der naheliegendste wäre an der Stelle Null:
bekomme ich durch einen Funktionswert, der naheliegendste wäre an der Stelle Null:
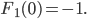
Rike Okay.
Charly Damit erhalte ich
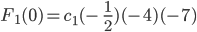
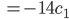
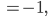
also
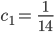
and in the end
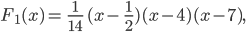
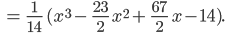
Rike Okay, das sieht gut aus.
Charly Die Funktion  erhalte ich durch Ableiten:
erhalte ich durch Ableiten:
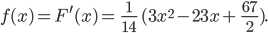
 für die Ableitung von
für die Ableitung von 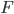 nach Charlys Polynom-Ansatz
nach Charlys Polynom-Ansatz
An der Stelle 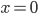 ergibt sich:
ergibt sich:
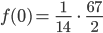
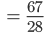
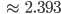
Rike Okay, das passt ja ungefähr zu meiner Schätzung von 2.
Das Integrationsintervall für das verschwindende Integral
Charly Für die nächste Teilaufgabe sollen reelle Zahlen 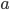 und
und 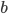 bestimmt werden,
bestimmt werden,
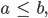
sodass
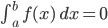
wird.
Rike Hey, du Anarchist, das ist doch trivial! Du wählst

Damit hast du für jede integrierbare Funktion  die Gleichung
die Gleichung
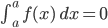
erfüllt. Du hast damit sogar unendlich viele Lösungen!
Charly Okay, du kleines Mathegenie, triviale Lösungen, die nur aus dem Kalkül kommen, verachten wir in der Schule.
Rike Haha, sehr witzig!
Berechnung nichttrivialer Lösungen
Charly Tatsächlich gibt es nichttriviale Lösungen, daran sitze ich gerade. Also, die Integralbedingung
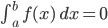
ist äquivalent mit der Eigenschaft
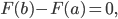
weil ja 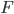 die Stammfunktion von
die Stammfunktion von  ist. Und weiter, diese Differenz kann ich berechnen:
ist. Und weiter, diese Differenz kann ich berechnen:
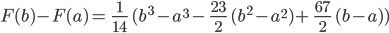
Da kannst du deine triviale Lösung 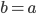 ausklammern und kriegst
ausklammern und kriegst
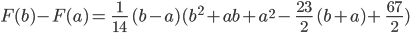
Rike Richtig.
Charly Die 1. Lösung ist
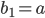
Die 2. und 3. Lösung 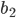 und
und 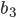 finden wir, wenn wir
finden wir, wenn wir
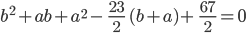
lösen. Mit der p-q-Formel und einfachen Umformungen habe ich die folgende Lösung erhalten:
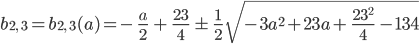
Rike Nicht schlecht für einen Anarchisten. Warte, für 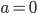 bekommst du 2 komplexe Lösungen
bekommst du 2 komplexe Lösungen 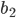 und
und 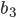 ...
...
Die schräge Ellipse
Charly Okay, du kleines Mathegenie, dann müssen wir prüfen, wann die Diskriminante 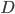 nichtnegativ wird:
nichtnegativ wird:
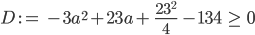
Die Division durch -3 auf beiden Seiten der Ungleichung ergibt die Ungleichung
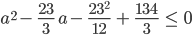
Mit der p-q-Formel kriege ich die Nullstellen  und
und  der Diskriminante:
der Diskriminante:
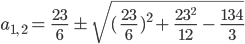
Rike, du Mathegenie, kannst du mir das mal ausrechen, ohne Rechner ist das heute nicht zu schaffen…
Rike Warte, klar, …, hier:
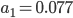
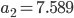
Charly Da für 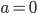 die Diskriminante negativ war, haben wir für
die Diskriminante negativ war, haben wir für
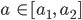
reelle Lösungen 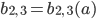 . Doch wie sehen die aus?
. Doch wie sehen die aus?
Rike Warte, ich zeichne dir die mal! Natürlich mit technischen Hilfsmitteln!
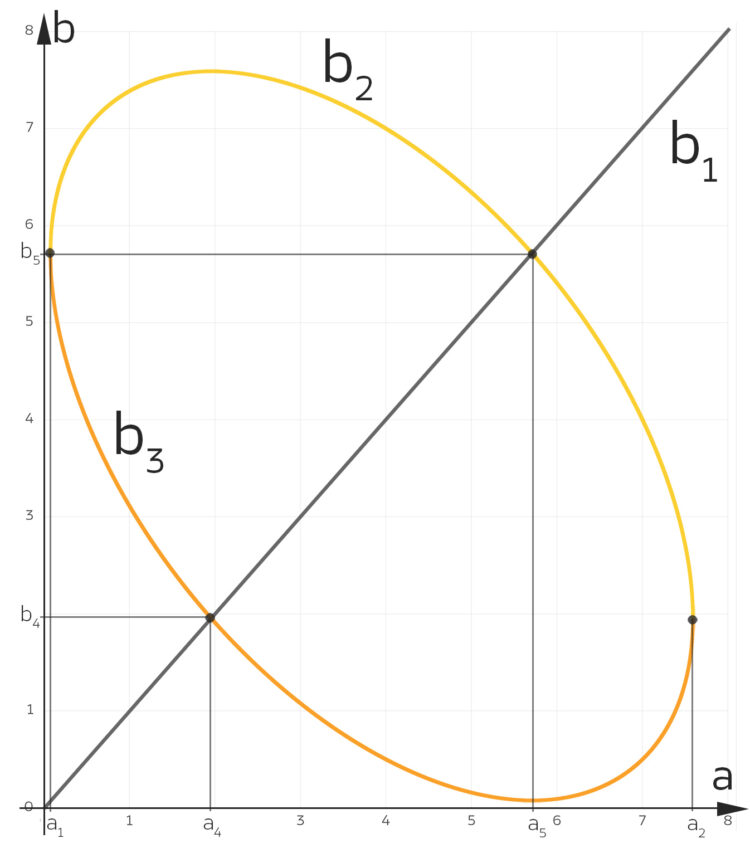
 in Abhängigkeit von
in Abhängigkeit von  .
.
Charly Wie eine schräge Ellipse! Das gefällt mir!
Die Intervallbedingung a ≤ b
Rike Wie eine schräge Ellipse. Die Intervallbedingung aus der Aufgabenstellung
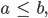
haben wir noch nicht berücksichtigt. Um genau die Grenzen zu finden, wo diese Bedingung verletzt wird, lass uns doch den „Rand“ der Gültigkeit in deine Ausgangsgleichung für die a-b-Abhängigkeit
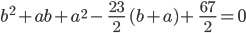
einsetzen. Aus dieser Gleichung wird mit 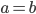 :
:
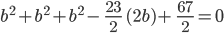
oder äquivalent dazu
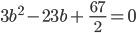
oder
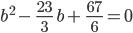
Charly Schon wieder brauchen wir eine p-q-Formel!
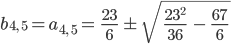
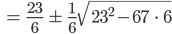
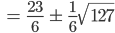
Das wären die Stellen, wo 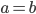 auf den Kurven
auf den Kurven 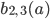 wird, hmm, sieht etwas kompliziert aus. Rike …
wird, hmm, sieht etwas kompliziert aus. Rike …
Rike Kein Problem,
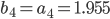
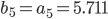
Charly Thanks!
Fall a ∈ [a1, a4]
Rike Tja, für 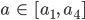 haben wir 2 Lösungen
haben wir 2 Lösungen 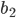 und
und 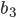 , sodass
, sodass
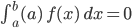
wird mit 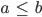 .
.
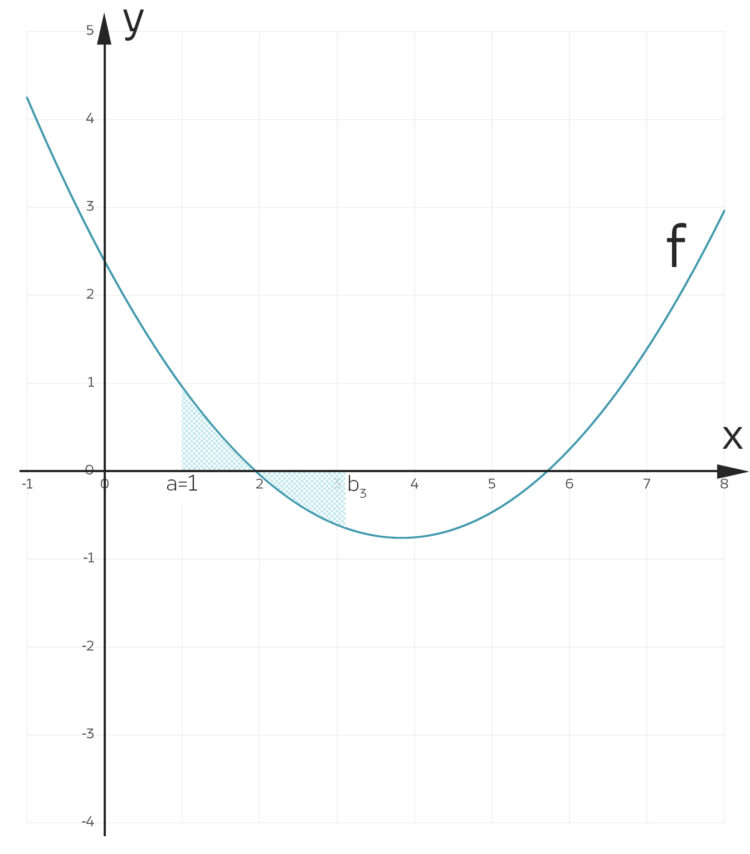
 und
und 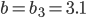 , sodass
, sodass 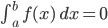
 und einem anderen
und einem anderen  für dieselbe Integralbedingung
für dieselbe IntegralbedingungFall a ∈ [a4, a5]
Charly Okay, für 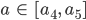 finde ich nur eine Lösung
finde ich nur eine Lösung 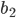 .
.
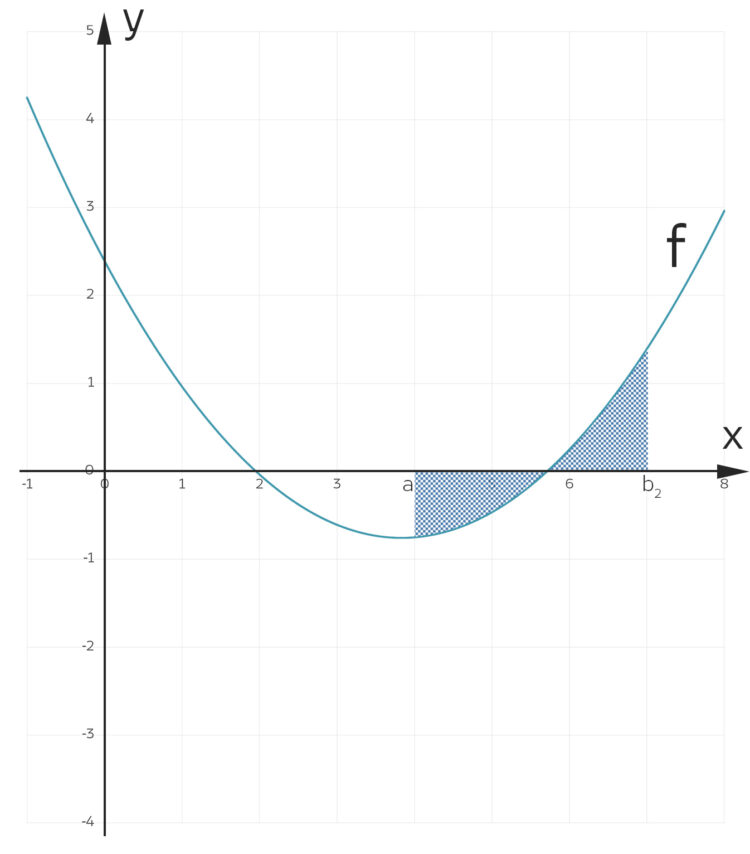
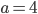 und
und 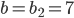
Restliche Fälle für a
Rike Für 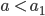 oder
oder 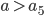 gibt es keine nichttrivialen Lösungen
gibt es keine nichttrivialen Lösungen 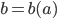 der Integrationsaufgabe
der Integrationsaufgabe
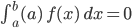
Charly Dank dir Rike, ohne dich hätte ich nie die schräge Ellipse gefunden!
Rike Haha.
***
Übungsaufgabe
Kann man die Funktion
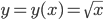
für 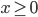 lediglich mit den 4 Grundrechenarten näherungsweise berechnen?
lediglich mit den 4 Grundrechenarten näherungsweise berechnen?
