KI-Variationen einer Klausuraufgabe

Rike kommt für einen kurzen Besuch an ihre ehemalige Uni, wo sie früher Mathetutorien gegeben hat. Sie lässt sich die neusten Matheklausuren zeigen. Die von der 3D-Darstellung von Funktionen zweier Veränderlicher hat es ihr besonders angetan. Wie schön die ist, seufzt sie.

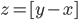B-2021-22-3d-klausur-WS-f-01-03 — Lösung der Aufgabe mittels Microsoft Excel und Bildbearbeitungsprogramm

Lösung der Aufgabe mittels Microsoft Excel und Bildbearbeitungsprogramm

Die Klausuraufgabe

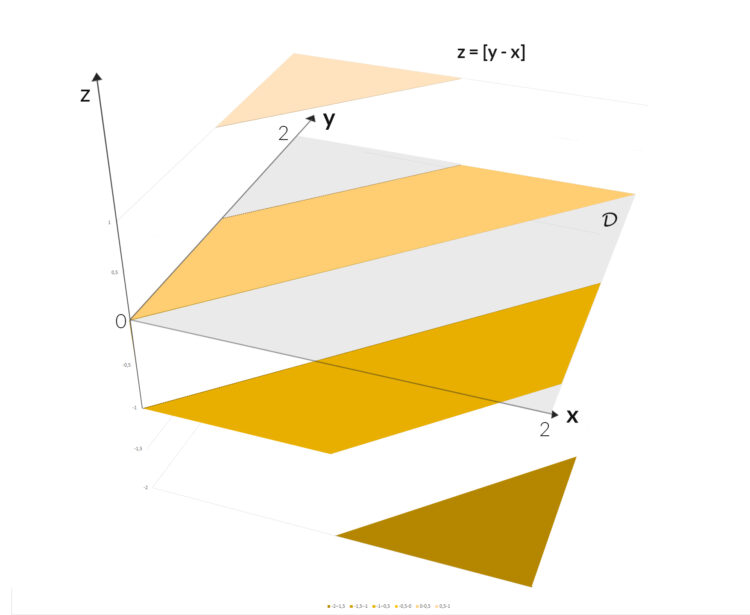
Eine unstetige Funktion ergibt eine unzusammenhängende Fläche. Außerdem sollte der Definitionsbereich :

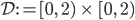
dargestellt werden. Der ist natürlich zusammmenhängend. Die Studenten und Studentinnen fragen Rike, wie wohl eine Variation dieser Aufgabe aussehen könnte. Da gibt es natürlich viele Möglichkeiten. Rike will mal wieder wissen, wie weit KI-Modelle sind, ob die auch schon Mathe-Klausuraufgaben variieren können. In der Abbildung der Lösung liegen alle Informationen vor: 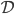und die Abbildungsvorschrift

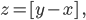
wobei die eckige Klammer für den ganzen Anteil einer reellen Zahl steht. Sie gibt diese Abbildung in DALL.E und erhält 3 verschiedene Variationen:

DALL.E-Variationen

DALL·E 2023-04-13_nr_1 — Variantion von DALL.E Nr. 1

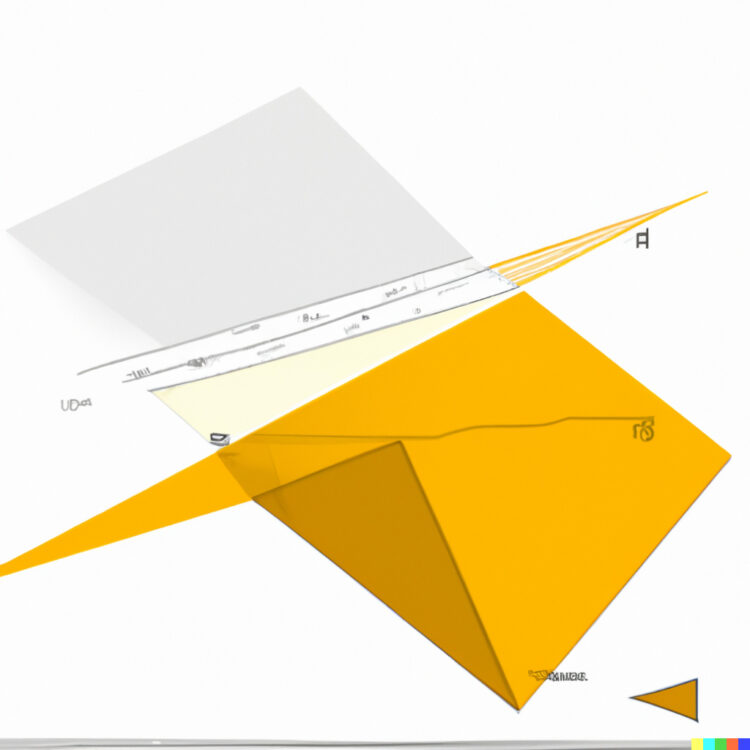
DALL·E 2023-04-13_nr_2 — 2. DALL.E-Variation „Zelt“

DALL·E 2023-04-13_nr_3 — Variantion von DALL.E Nr. 3

3D-Funktionsdarstellung

Bei der 2. überlegt sie, ob dies überhaupt eine „sinnnvolle“ Fläche ist, die durch eine Vorschrift

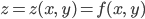
berechnet werden kann. Zu Hause zeigt sie Charly das Bild.

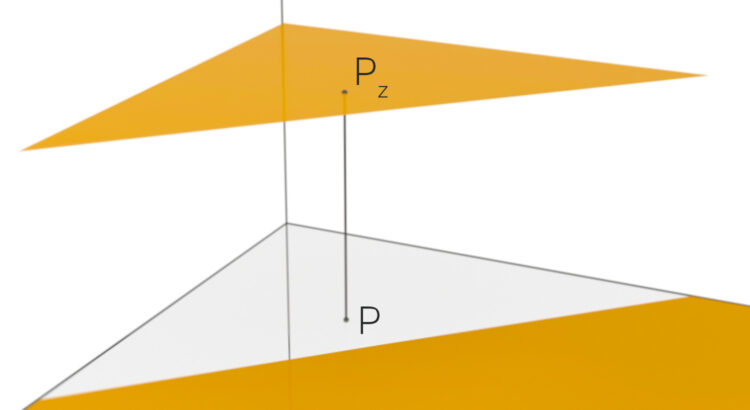
Charly Offensichtlich hat die KI das untere Dreieck aufgegriffen und prominent untergebracht. Die Fläche kann ich auch entdecken, allerdings nicht in ihrer Eigenschaft als Definitionsbereich. Du willst doch eigentlich jedem Punkt

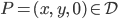
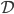
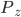
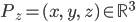
aus dem Definitionsbereich einen Punkt

zuordnen, wo

ist. Der liegt dann über dem Punkt . Hört sich etwas umständlich an, sorry, aber stimmt’s?

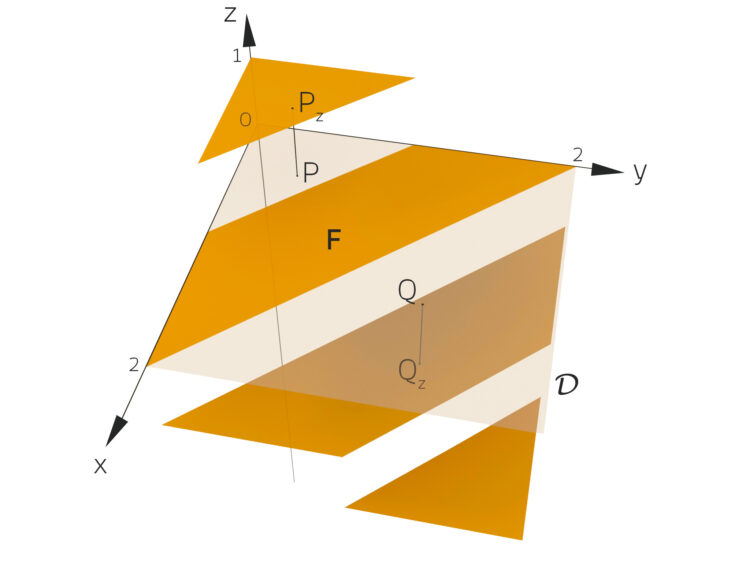
04_2023_render_flaeche_35_04 — Abbildung zur Zuordnung der Punkte bzw. .

Abbildung zur Zuordnung der Punkte bzw. .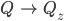

Geometrie des DALL.E-Zeltes

Rike Ja, richtig. Charly, weißt du, die 2. Fläche sieht wie ein Zelt aus, die vordere Ecke ist hochgeklappt. Meinst du, ich kann dieses Zelt aus einer „Zeltplane“ konstruieren?

Charly Ja, ich glaube schon, es ist so eine Art ebenes 6-Eck, ein Dreieck entfernst du, eins biegst du nach oben.

04_2023_6-Eck — Charlys 6-Eck zur Konstruktion der Fläche von DALL.E

Rike Okay, warte, ja, hier… Ich muß die Eckpunkte etwas verschieben, aber das ändert die Topologie nicht.

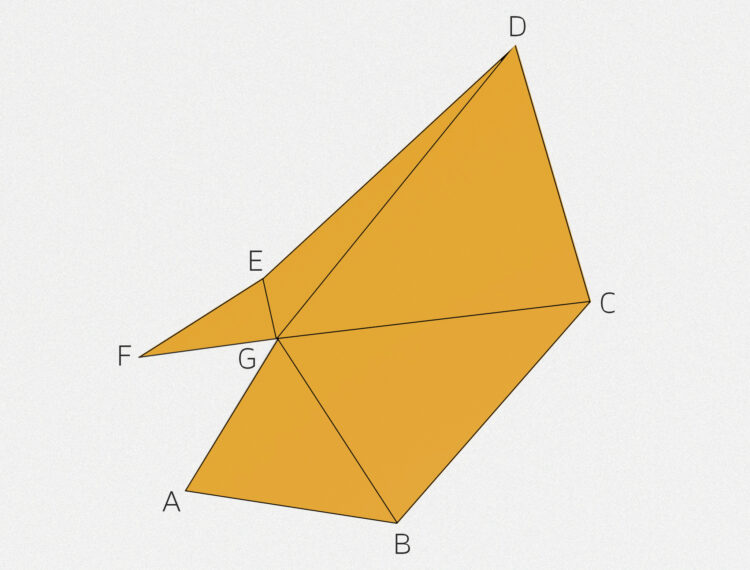
04_2023_render_top_34_04 — Stetige Änderungen der Punkte des 6-Ecks

04_2023_render_32_03 — Perspektivische Ansicht des Zeltes aus dem 6-Eck

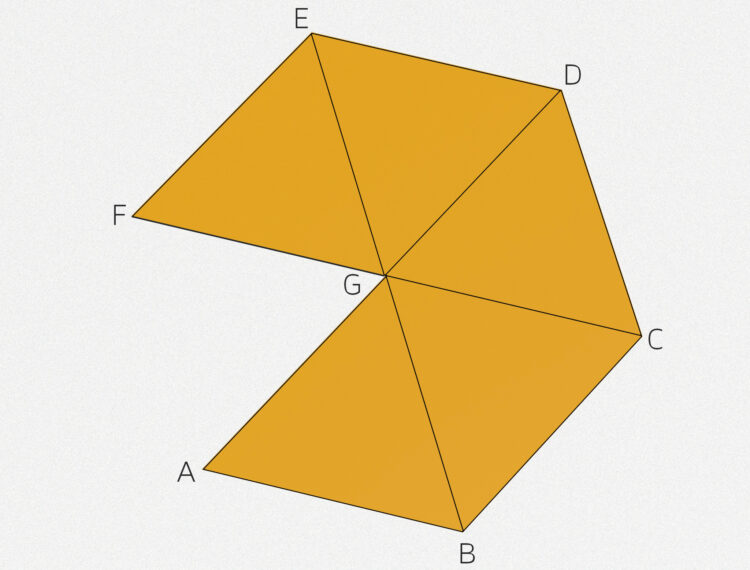
Jetzt ziehe ich den Punkt 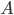nach oben und außerdem den Punkt 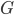auch etwas nach oben, um die Kante 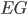zu erzeugen.

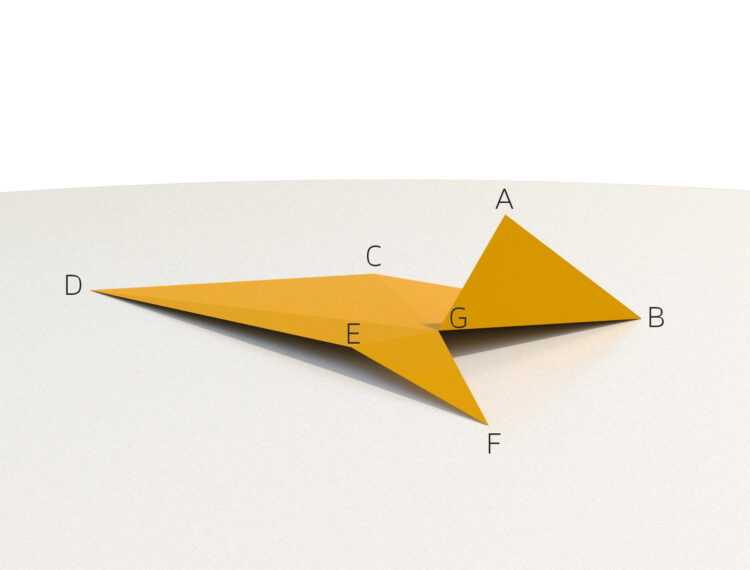
04_2023_render_A_32_03 — Andere perspektivische Ansicht des Zeltes

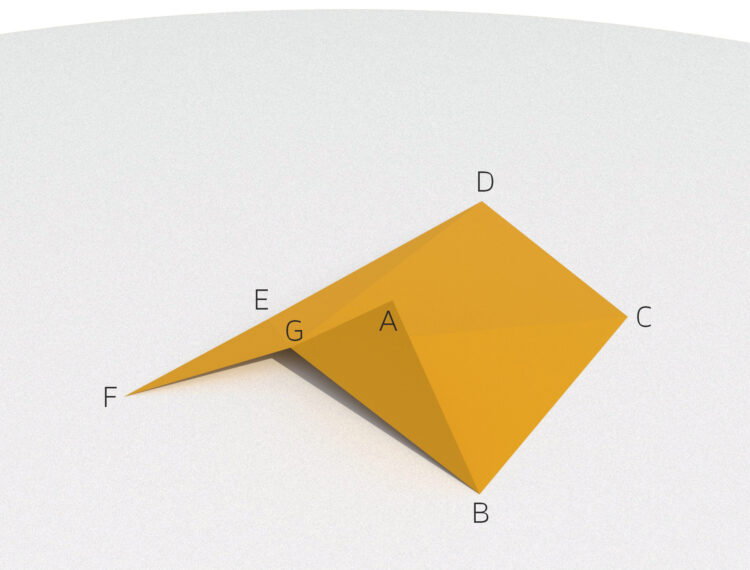
Charly Okay, Rike, genau das DALL.E-Zelt! Super! Die Geometrie ist also klar, es besteht aus 5 zusammenhängenden Dreiecken.

Rike Aber weißt du, was mir auffällt, diesen Schatten an der Kante 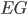in Richtung D bekomme ich nicht gleichzeitig mit der uns zugewandten Seite des Dreiecks 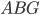hin! Jedenfalls, wenn ich nur eine Lichtquelle benutze!

Charly Okay! Physikalische Korrektheit ist wohl nicht die größte Stärke von KI-erzeugten Bildern?

Rike Haha, leider nicht!

Charly Dann wäre ja eine kritische Interpretation dieser KI-Variante vielleicht eine witzige Klausuraufgabe für Medienproduzenten?

Rike Charly, ja, das ist eine tolle Idee, da kann ich gleich mal in Ostwestfalen anrufen!

Das DALL.E-Zelt als Funktionsdarstellung

Übungsaufgaben

Ist das Zelt eine Fläche der Form: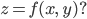
Was ist mit den anderen Varianten, greifen die Eigenschaften der ursprünglichen Aufgabe auf?

Lösungen

Nein, die um über 90° hochgeklappte Fläche 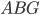befindet sich über der Fläche 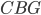, sodass den Punkten darunter 2 Höhen 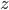zugewiesen werden müssten.
Die Varianten 1 und 3 zeigen Oberflächen von Körpern, die ebensfalls nicht in einer geschlossen Form als Funktion beschrieben werden können.