Rike und Charly haben sich vorgenommen, als Alternative zur Trainingsstrecken-Aufgabe selbst eine übersichtliche und anwendungsnahe Abiaufgabe zu entwerfen. Geht das zum Thema Skilauf? Charly hat die Idee, kleinere Sprungschanzen, die manchmal zu Skiabfahrtpisten dazugehören, zu untersuchen. Vor allem die Landebahnen dazu sollen wie „richtige“ Skischanzen den gängigen Standards genügen. Er schlägt vor, dass die Schüler und Schülerinnen eine parameterabhängige Kurve p3(x) mit den folgenden Eigenschaften bestimmen:
Eigenschaften der Landebahnkurve
Die Kurve p3(x) ist ein Polynom 3. Grades:
p3(x) = ax³ + bx² + cx + d.
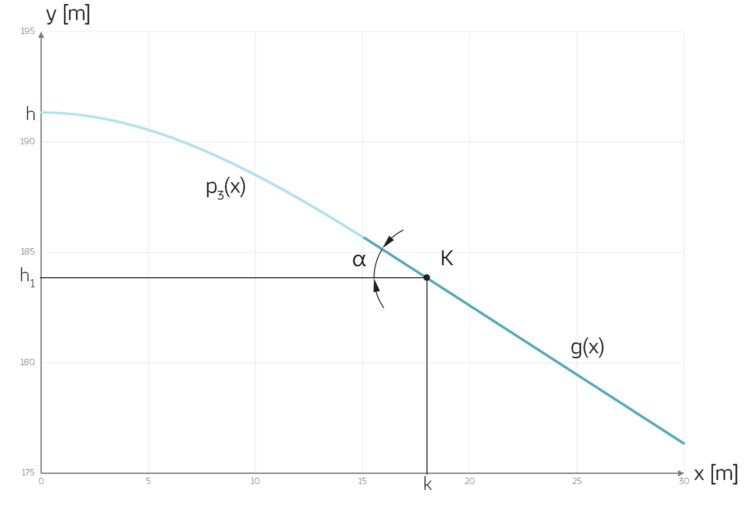
Sie ist für x zwischen 0 und 30 Metern definiert. An der Stelle x = 0 nimmt sie die Höhe h > 0 an, die Ableitung an dieser Stelle soll verschwinden. Eine wichtige Besonderheit ist, dass es einen „Konstruktionspunkt“ K gibt:
K = (k, h1),
wo die Kurve in eine Gerade g übergeht. Für ihn sollen gelten:
k, h1 > 0,
h > h1.
Dabei sind im Punkt K Anstieg und Krümmung des Polynoms p3 und der Gerade g jeweils gleich. Der Anstieg ist gegeben durch den Winkel α, α liegt zwischen 0 und 90°, siehe Abb. 1.
Charlys Aufgabe 1. Teil
a) Beschreiben Sie die Bedingungen an das Polynom p3(x) formal!
b) Bestimmen Sie a, b, c, d in Abhängigkeit von h, k und dem Winkel α!
c) Bestimmen Sie a, b, c, d für
k = 18 m,
h = 191,34 m,
α = 32°.
d) Stellen Sie Ihre Kurven p3(x) und g(x) aus c) grafisch dar!
Über der Landebahn mit der Höhe h ist eine Schanze mit dem Absprungpunkt in der Höhe h2 > h. Der Sportler oder die Sportlerin versucht, möglichst weit zu springen und sicher zu landen. Die Kurve des Sportlers oder der Sportlerin ist gegeben durch
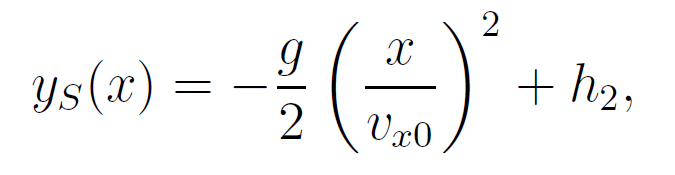wobei vx0 die waagerechte Geschwindigkeitskomponente beim Absprung ist und
g = 9,81 m/s²
die Erdbeschleunigung ist, siehe Abb. 2. Die Geschwindigkeitskomponente in die senkrechte Richtung wird in dieser Aufgabe vernachlässigt.
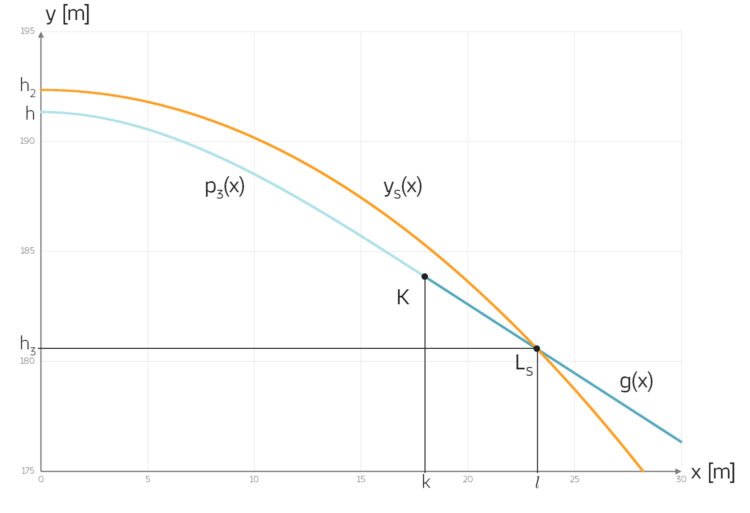
e) Bestimmen Sie zu Ihrer Kurve aus c) ein Paar geeignete Parameter h2 und vx0 näherungsweise, sodass der Schnittpunkt LS von p3(x) oder g(x) mit yS(x):
LS = (l, h3)
innerhalb des Definitionsbereiches liegt:
0 < l < 30 m.
f) Bestimmen Sie näherungsweise die x-Koordinate l vom Schnittpunkt LS!
Rikes und Charlys Diskussion zu Hilfsmitteln und Anzahl der Lösungen
Rike Charly, das gefällt mir, sehr sportlich!
Charly Danke!
Rike Wenn der Landepunkt LS nicht festgelegt ist, gibt es viele Parameter h2 und vx0, die die Aufgabe e) lösen?
Charly Stimmt. Das wäre mal eine Aufgabe, wo es von vornherein mehrere Lösungen gibt. Es ist kein Problem für mich, das zu korrigieren.
Rike Am besten benutzt man dazu ein grafikfähiges Tabellenkalkulationsprogramm, richtig?
Charly Stimmt, damit kann man die Aufgabe grafisch lösen.
Rike Dazu muss erst ein neues Zeitalter im Bildungswesen beginnen!
Charly Die Hoffnung stirbt zuletzt, heißt es so?
Rike Haha! Ich glaube, es fehlt noch die Integrationsaufgabe.
Die Integrationsaufgabe
Charly Warte, Rike, die habe ich! Die Schüler und Schülerinnen sollen die Flugweite bestimmen!
Rike Hmm, die Länge eines Funktionsgraphen, ist das nicht etwas anspruchsvoll? Das ergibt kein Standardintegral.
Charly Ich weiß, es ist auch in der Realität schwierig, die Flugweite zu messen. Ich schlage vor, wir geben die Formel an, damit die Abiturienten sie mit ihrem Taschenrechner oder näherungsweise ermitteln. Das entspricht zwar schon wieder nicht den Vorstellungen des Ministeriums, aber wenn man die Flugweite halbwegs genau berechnen kann, dann hat man doch das Integral verstanden, oder?
Rike Richtig. Doch ich glaube, du machst dich mit solchen revolutionären Ideen bei deinen Kollegen und dem Chef total unbeliebt. Du handelst dir ziemlichen Ärger ein.
Charly Tja... Weißt du was, ich zeige die Aufgabe meinen Schülern, meinen Schülerinnen natürlich auch (mit einem Augenzwinkern) und vor allem besprechen ich sie mit den Wintersportler:innen unter ihnen.
Rike Gute Idee, Charly!
Charly Gut, ich würde die Aufgabe so formulieren:
Charlys Aufgabe 2. Teil
g) Bestimmen Sie nach der folgenden Formel die Flugweite W
für Ihre Kurve yS(x) aus e) und f) näherungsweise oder mit dem Taschenrechner!
Lösung
a)
p3(0) = h
p3’(0) = 0
p3”(k) = 0
p3’(k) = ‒ tan α
b)
c) a = 0,00064287/m², b = ‒ 0,034715/m; c = 0, d = 191,34 m
d) siehe Abb. 2
e) h2 = 192,34 m, vx0 = 15 m/s
f) l = 23,22 m
g) W = 26,73 m