Charly sitzt an diesem verregneten und windigen Osterferientag an einer „sportlichen“ Abiaufgabe. Es ist eine typische Analysis-Aufgabe über eine Funktionenschar mit einem Parameter. In dieser Aufgabe werden Nullstellenberechnung, Flächenberechnung, Kurvendiskussion, topologische Eigenschaften, numerische Näherungsverfahren, Zahlentheorie und nicht zuletzt eine Anwendung kombiniert. Die Aufgabe, die einen wissenschaftlichen Taschenrechner als Hilfsmittel zulässt, hat 13 Teilaufgaben. Man kann insgesamt für die Aufgabe 50 Punkte erhalten. Da kommt Rike dazu.
Rike Hey Charly, was ist denn los?
Charly Rike, gut, dass du kommst. Schau dir mal die Abiaufgabe vom letzten Jahr an!
Rike Hey, warte, was, 3 Seiten und Teilaufgaben von a) bis p)?
Charly Genau! Der sportliche Bezug ist sooooo schwach, dass er für meine Schülerinnen und Schüler keine Motivation bildet. Gerade die Skifahrer unter ihnen lachen darüber und ich stehe wie ein Idiot da.
Rike Hmm.
Visualisierung einer Funktionenschar
Charly Aber weißt du, am schwierigsten ist es, sich die Funktionenschar vorzustellen. Erst dann kann man Schritt für Schritt alle Eigenschaften berechnen, prüfen und verstehen.
Rike Richtig!
Charly Ohne eine visuelle Vorstellung alle Teilaufgaben abzuarbeiten, macht wenig Spaß und überzeugt nicht. Und hier fangen die Schwierigkeiten an: Der Graph der Funktionenschar heißt Ga. Dabei ist a der Parameter. Außerdem gibt es einen Graphen Gh, auf dem alle Extrempunkte liegen.
Rike Wofür steht h? Ist das auch ein Parameter?
Charly Nein! Er steht für die Funktion h, auf der die Extremwerte liegen.
Rike Das ist wirklich eine unglückliche Bezeichnung. Weißt du, obwohl ihr keinen grafikfähigen Rechner benutzen dürft, überlegen wir trotzdem mal, wie die Kurvenschar aussieht. Vielleicht könnt ihr das in der Stunde diskutieren und einige wichtige Werte in Gruppenarbeit ausrechnen?
Charly Ja, das ist eine gute Idee! Wir machen eine riesige Wertetabelle und stärken dabei die Teamkompetenz, haha!
Rike Also – wie heißt die Funktionenschar?
Charly
fa(x) = (4a – x) ∙ ex/2
Rike Okay. Welche Werte kommen denn für a in Betracht?
Charly Zunächst steht hier, dass a reell ist, außerdem soll
a ≠ 0.
Rike Warum ist denn
a ≠ 0?
Charly Weiß ich nicht, in den weiteren Teilaufgaben kommen die Werte
a = 1
und
a = 0.5
vor.
Rike Okay, dann berechne ich mal mehrere Kurven für diverse Werte von a:
a = –1, –0.5, 0, 0.5, 1.
Vor allem a = 0 interessiert mich!
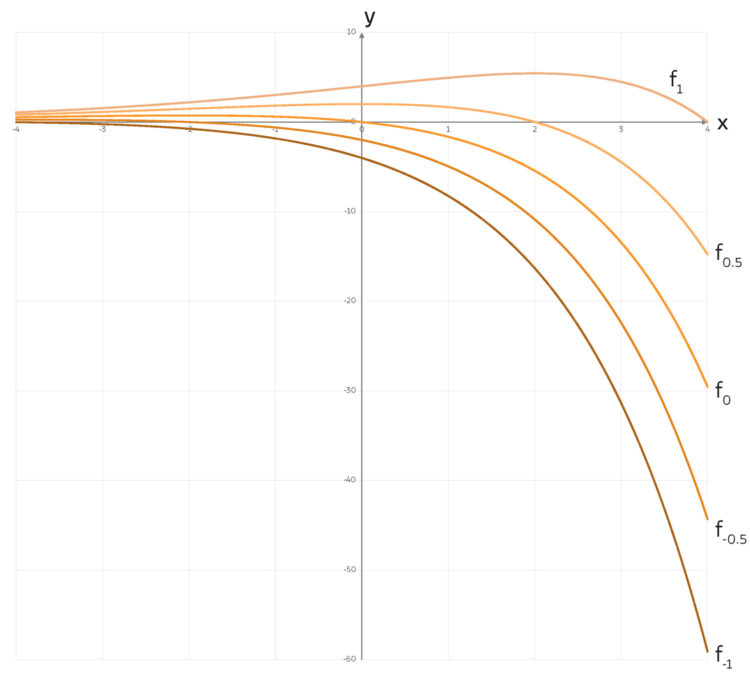
Charly Okay. Die Kurven hängen doch stetig von a ab. Kannst du auch die Fläche für alle
a ∈ [–1, 1]
zeichnen?
Rike Ja, klar!
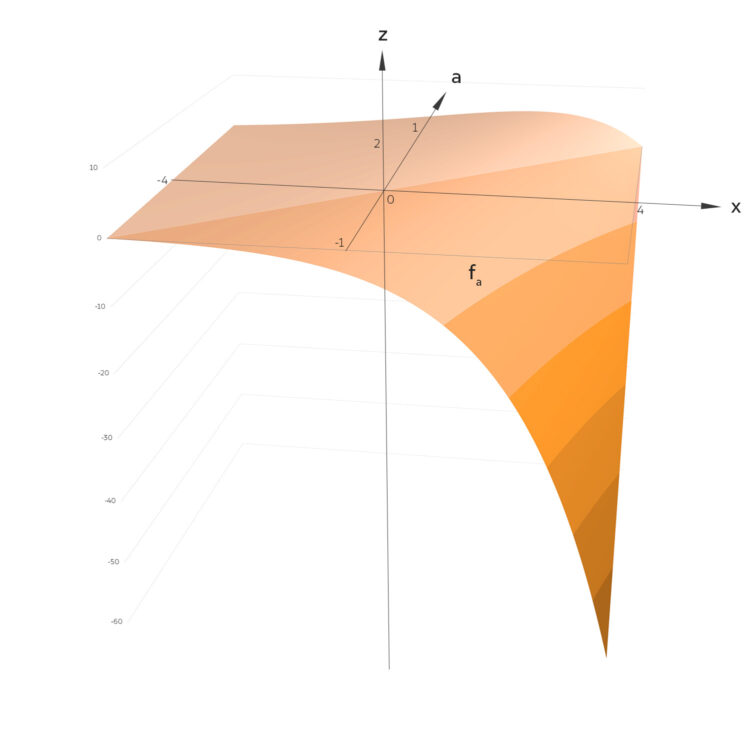
Charly Rike, das sieht ja geil aus!
Rike Danke!
Charly Warum a = 0 verboten wird, kann ich nicht verstehen, dann kriegt die Fläche fa ja eine Lücke und ist nicht mehr zusammenhängend???
Rike Ja, lass uns einfach a = 0 nicht ausschließen.
Nullstellen der Funktionenschar
Charly Jetzt kommen die Nullstellen. Das ist nicht schwer, das ist da, wo
4a – x = 0
Rike Stimmt. Schau, hier ist die Fläche fa im dreidimensionalen Raum mit einem kartesischen Koordinatensystem, wo die Koordinaten üblicherweise mit x, y und z bezeichnet werden. Jetzt übernimmt a die Rolle von y. Wenn wir also deine Gleichung nach a auflösen, kriegen wir
a = x/4
Das ist eine Gerade, die ist bei mir schon farblich hervorgehoben.
Maxima der Funktionenschar
Charly Gut, ich verstehe das und sehe auch die Linie der Nullstellen. Jetzt noch die Maxima. Warte, hier die 1. Ableitung ist
f 'a(x) = (–x/2 + 2a – 1) ∙ ex/2
Die wird Null für
–x/2 + 2a – 1 = 0
oder
x = –2 + 4a
Und für dich kann ich das auch nach a auflösen:
a = x/4 + 1/2
Rike Gut, das sind Geraden, die kann ich gut einzeichnen. Und über der Geraden
a = x/4 + 1/2
liegen alle Maxima fmax von fa?
Charly Genau. Zeig mal!
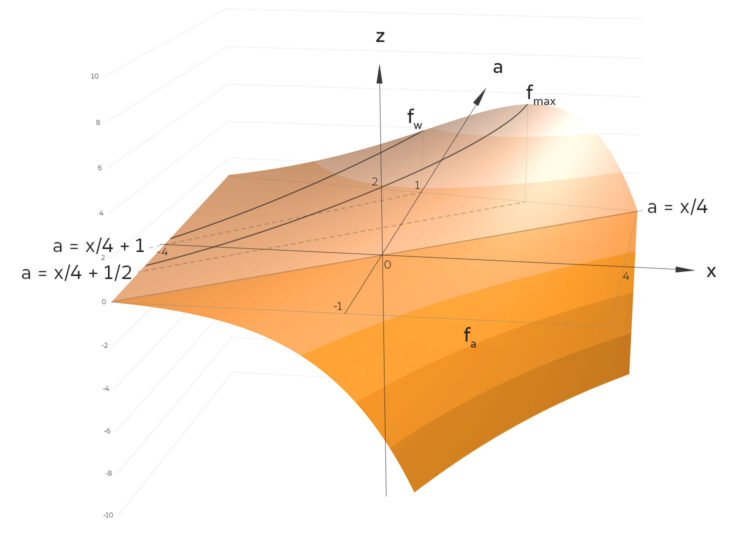
Finales Bild
Rike Hier!
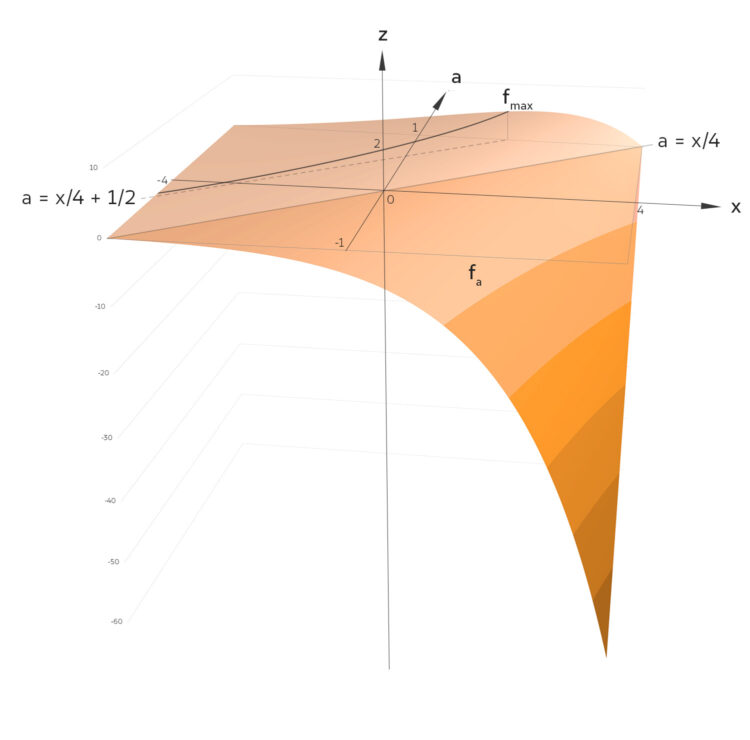
Charly Okay, Rike, super. Jetzt kann ich mir Alles gut vorstellen!!! Gh ist dein fmax! So können wir die Aufgabe gut besprechen. Ich muss nur richtig anfangen.
Rike Sag mal, Charly, die Fläche fühlt sich rechts vorn wie ein schwarzes Loch an??? Ist das die Trainingsstrecke?
Charly Hahaha! Die zeige ich dir gleich, wir müssen erste noch eine weitere Teilaufgabe lösen!
***
Übungsaufgabe
Berechne die 2. Ableitung und zeichne die Linie der x-Werte für die Wendepunkte (x, a, 0) als auch die Kurve fw der Wendepunkte in die Fläche ein!
Lösungen
f "a(x) = (–x/4 + a – 1) ∙ ex/2