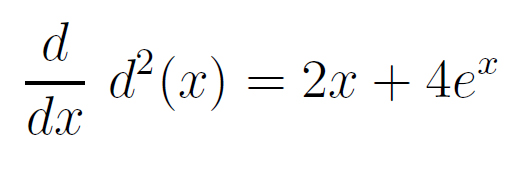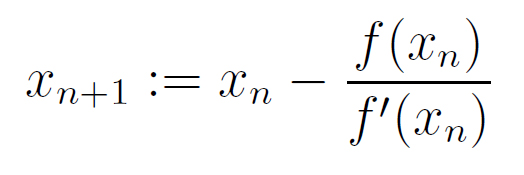Rike hat in Erwartung der Berechnung einer Skipiste in einer abwechslungsreichen Landschaft mit starken Abfahrten ins Ungewisse die ganze Nacht vom Skifahren geträumt. Sie ist immer wieder ins "schwarze Loch" gefahren und mehrfach hochgeschreckt. (Charly hatte ihr zwar das File mit der Aufgabe nicht gegeben, aber sie dann doch irgendwie beruhigt.) Ob sie wohl die Länge der Strecke ins "schwarze Loch" ausrechnen soll? Oder die Geschwindigkeit eines Skifahrers oder den Abstand von zweien?
Charly Nein, Rike, diese Abfahrt für große x und negative a brauchst du nicht zu fahren! Die Strecke auf dem Höhenzug fmax, den du ausgerechnet hast, ist doch viel schöner: freier Blick nach vorn, rechts und nach links, das ist die allerbeste Piste!
Rike Okay, fmax ist die allerbeste Piste! Charly, nun sag schon, was ist die nächste Teilaufgabe? Ich hätte tausend verrückte Vorschläge!
Die verrückte Teilaufgabe
Charly So verrückt kannst du gar nicht denken!
Rike Doch!
Charly Also – es ist etwas umständlich formuliert, aber im Grunde soll der kürzeste Abstand von der Kurve fmax auf der Fläche fa zum Nullpunkt näherungsweise bestimmt werden!
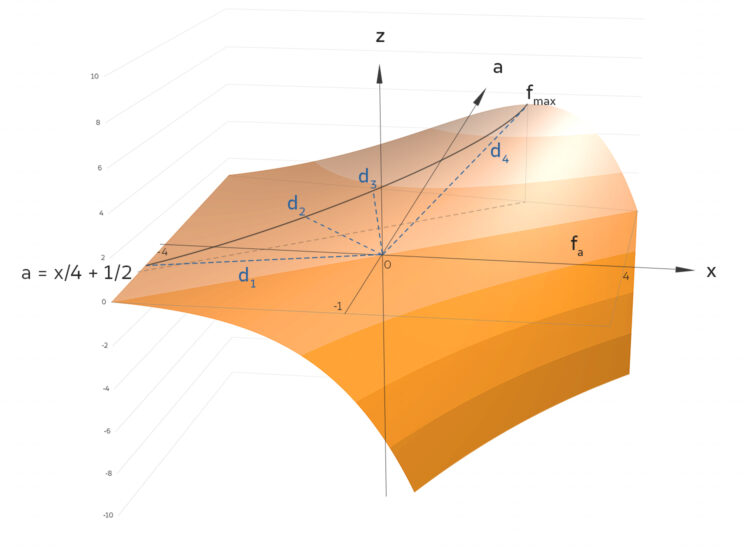
Rike Aha! Soll da ein Tunnel gegraben werden, sind da die Ruinen von Atlantis?
Charly Haha, ja, so ungefähr!
Rike Na, super. Findest du die Aufgabe angemessen? Du als Mathelehrer und Quereinsteiger?
Charly Ich finde sie unglücklich formuliert, vieles irritiert mich. Der Zusammenhang von x und a auf der Kurve fmax ist mir selbst nicht klar – ich meine, die Kurve liegt schräg im dreidimensionalen Raum! Sie erfordert räumliches Vorstellungsvermögen, von mir, von meinen Schülern und Schülerinnen, das erfordert Zeit und Materialien dazu, ich brauche Verständnis und Entgegenkommen verschiedener Entscheidungsträger, um es mal vorsichtig zu formulieren…
Rike Stimmt. Aber wir beide lösen das jetzt, wir versuchen‘s jedenfalls, in deinem Buch steht ja wohl auch eine Lösung?
Charly Ja, da steht eine. Doch ich verstehe sie nicht.
Berechnung der Funktionswerte von fmax
Rike Okay. Lass uns einfach die Kurve fmax genauer betrachten, dann den Abstand ausrechnen und minimieren, wie eine Kurvendiskussion.
Charly Sehr gut. Das machen wir.
Rike Also, die Funktionenschar ist gegeben durch die Formel
fa(x) = (4a – x) ∙ ex/2
Diesen Ausdruck hatten wir abgeleitet und die Gerade
a = x/4 + ½
gefunden, wo das notwendige Kriterium
fa'(x) = 0
erfüllt ist.
Charly Richtig.
Rike Soweit, so gut. Für diese a-Werte rechnen wir die Funktionswerte aus, sie liegen ja auf fa:
fmax(x) = (4a – x) ∙ ex/2
= (4(x/4 + ½) – x) ∙ ex/2
= 2ex/2
Charly Okay, verstehe! Das können wir wie eine normale Funktion zeichnen, in Wahrheit liegt sie schräg in der Fläche fa.
Der Abstand zum "Mittelpunkt der Erde"
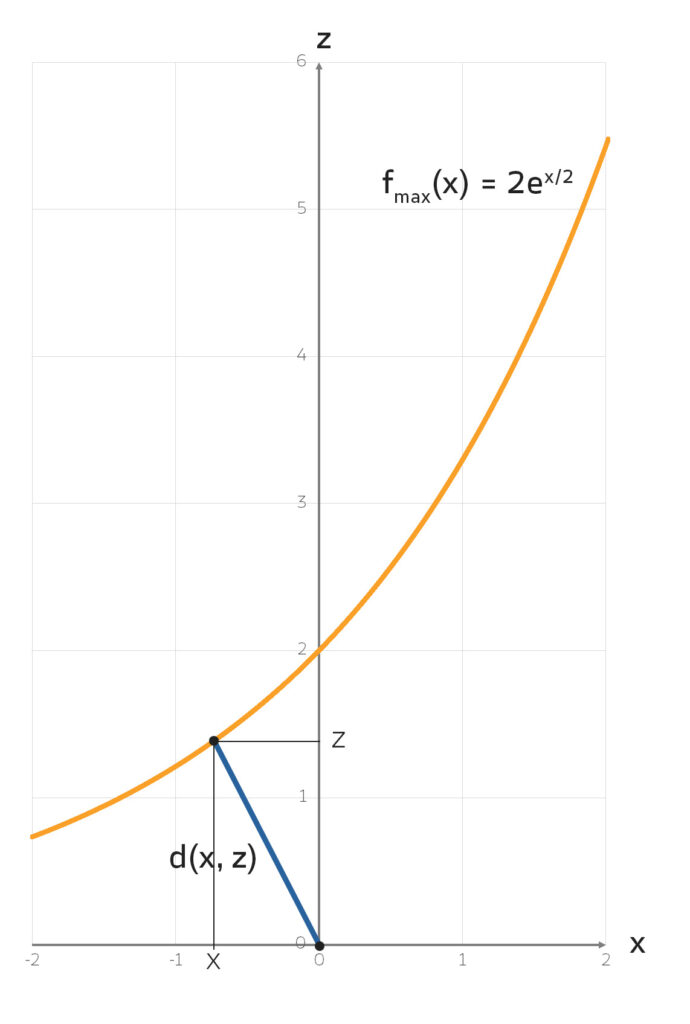
Rike Jetzt kommt der Abstand zum Nullpunkt!
Charly Ich würde den Satz des Pythagoras nehmen und nicht das Lot vom Mittelpunkt auf die Kurve fällen.
Rike Ich auch! Lass uns den quadratischen Abstand d2 nehmen. Das erleichtert die Rechnung.
Charly Okay! Sowas habe ich zwar noch nie gemacht, aber es erleichtert wirklich die Rechnung!
Rike
d²(x, z) = x² + z²
= x² + (fmax(x))²
= x² + (2ex/2 )²
= x² + 4ex
= d²(x)
Charly Okay, der Abstand hängt entlang der Kurve fmax nur noch von x ab.
Rike Jetzt suchen wir das Minimum von d²!
Charly Okay, wir leiten diesen quadratischen Abstand einmal ab:
So, diese Ableitung soll Null werden, als notwendiges Kriterium fürs Minimum kriege ich:
Notwendige Bedingung für den minimalen Abstand d
Das können wir durch 2 teilen und erhalten als Bedingung:
x + 2ex = 0
Rike Gut so. Lass uns nun diesen Ausdruck in einer Funktion f formulieren:
f(x) = x + 2ex.
Für diese Funktion f suchen wir eine Nullstelle xd. Das ist eine nichtlineare Aufgabe. Mit Standardmethoden kommt man da nicht weit. Das können wir numerisch lösen. Habt ihr sowas schon mal gemacht?
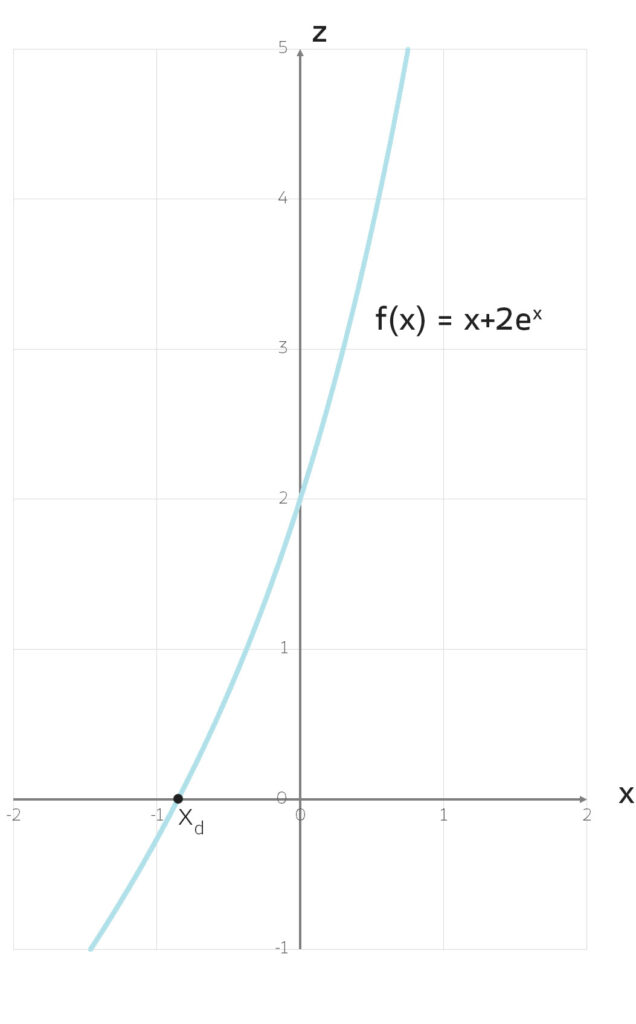
Charly Naja, wir haben kurz das Newton-Verfahren behandelt. Im Lehrbuch von Bigalke & Köhler ist das Verfahren gut beschreiben, der Fokus liegt allerdings auf dem Finden des Startwertes x0.
Newton-Verfahren für die Nullstelle von f
Rike Ja, stimmt, zeig mal euer Buch: Aha, der Startwert soll so genau wie möglich gefunden werden. "Dann kann man mit der nebenstehenden Formel eine neue Näherung xn+1 errechnen, die in der Regel besser ist als xn"! Haha! In der Regel!
Die Voraussetzungen für f(x) finde ich nicht.
Charly Was erwartest du denn! Es ist eine Art Glücksspiel.
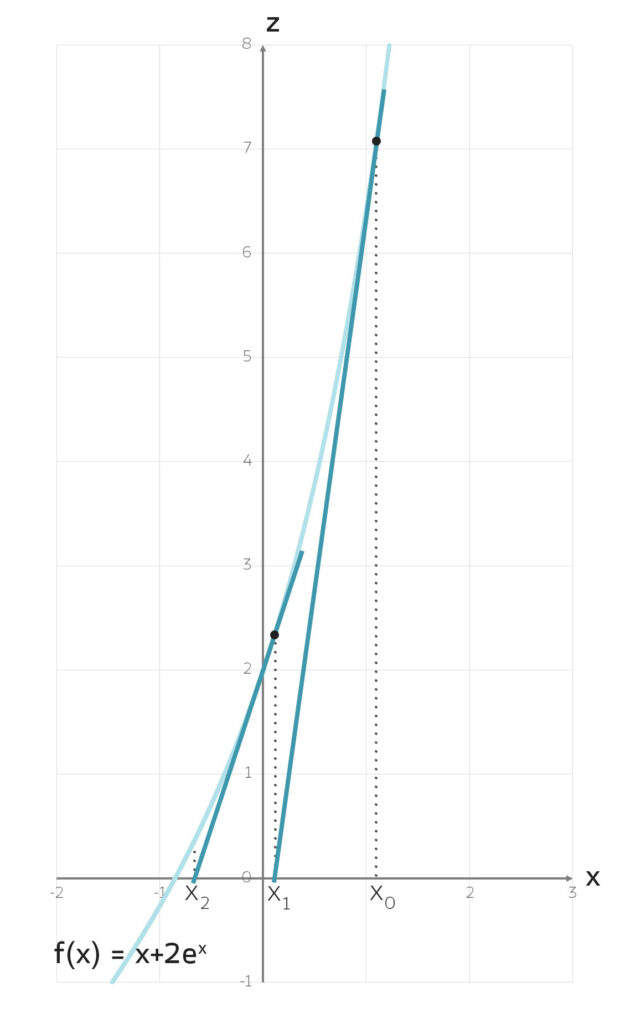
Rike Schau mal, wenn ich den Startwert x0 rechts von der zu suchenden Nullstelle wähle, zum Beispiel
x0 = 1,
f(x0) > 0,
dann sind alle Voraussetzungen des Newton-Verfahrens (f ∈ C1, f ‘(x0) ≠ 0) erfüllt bis auf die Bedingung, dass der Abstand von x0 zur Nullstelle xd sehr klein ist:
|x0 – xd| « 1.
Aber trotzdem konvergiert das Verfahren!
Besonderheiten der Funktion f und Auswirkungen auf das Verfahren
Charly Das muss an der Form der Funktion f liegen. f ist konvex und streng monoton wachsend.
Rike Ja, stimmt. Warte, ich schau mal im Internet, …, hier, …, ich habe was: Wenn f zweimal stetig differenzierbar sowie konvex in einem Intervall [a, b] ist und dort genau eine Nullstelle hat, dann kann ich jeden beliebigen Startwert
x0 ∈ [a,b]
mit
f(x0) > 0
wählen. Das Verfahren konvergiert. Man kann sogar die Konvergenz näher beschreiben. Sie ist quadratisch.
Charly Das ist gut für die Aufgabe: Dass das Verfahren konvergiert, dass es genau eine Nullstelle gibt. Das können dann die Schüler und Schülerinnen direkt berechnen oder das SOLVE-Tool des wissenschaftlichen Taschenrechners benutzen.
Rike Schön, das Tool schaue ich mir gleich an. Das direkte Ausrechnen nach der Newton-Formel können wir jetzt gleich machen. Sollen wir mit dem Anfangswert
x0 = 1
starten und die Entfernung zum Mittelpunkt der Erde berechnen?
Erwartungshorizont
Charly Okay! Es ist nicht genau das, was erwartet wird, aber wir finden bestimmt die Lösung.
Rike Was wird denn erwartet?
Charly Den Startwert bei
x0 = –0.8
zu wählen.
Rike Dazu brauchst du eine sehr gute, hoch aufgelöste grafische Darstellung der Funktion f(x)! Außerdem ist das gar nicht nötig! – Wie gehst du denn damit um? Würde ich dann bei dir die volle Punktzahl kriegen mit meinem Startwert x0 = 1?
Charly Hey, ich liebe es, wenn du diese Frage stellst.
Rike Das ist keine Antwort.
Charlys Fazit
Charly Naja, die Trainingsstrecken-Aufgabe hat keinen Lebensweltbezug. Der Erwartungshorizont ist jenseits mathematischer Straightforward Strategien, so wie du sie nutzt, und die zu vermittelnden Kompetenzen kriege ich jetzt auch nicht zusammen…
Rike Machst du Scherze? Was soll das?
Charly Ich mache mir schon Sorgen ums Matheabi.
Rike Aber du verzweifelst nicht?
Charly Irgendwie scheint mir, dass man mit einem ordentlichen Mathestudium, einer ganz neuen Formulierung der Trainingsstrecken-Aufgabe, einem Tabellenkalkulationsprogramm und einem wissenschaftlichen Taschenrechner die Entfernung zum Mittelpunkt der Erde sehr gut berechnen kann! Kein Grund zum Verzweifeln!
Rike Sag ich doch!
Charly küsst Rike.
***
Übungsaufgaben
- Berechne die Nullstelle xd bis auf 4 Stellen nach dem Komma genau.
- Berechne den Parameter a dazu.
- Überprüfe die Konvexität der Funktion f.
Lösungen
1.
| n | xn | f(xn) |
| 0 | 1.0000 | 6.4366 |
| 1 | 0.0000 | 2.0000 |
| 2 | -0.6667 | 0.3602 |
| 3 | -0.84437 | 0.0153 |
| 4 | -0.8526 | 0.0000 |
Die 4. Näherung von xd hat bereits die geforderten 4 Stellen Genauigkeit:
xd = -0.8526
2.
a = a(x) = x/4 + ½
a(xd) = xd/4 + ½
= -0.8526/4 + 0.5000
= 0.2869
3. Die Funktion f(x):
f(x) = x + 2ex.
ist konvex, wenn ihre Ableitung monoton wachsend ist, siehe Wikipedia. Die 1. Ableitung f '(x) von f(x):
f '(x) = 1 + 2ex
ist monoton wachsend, wenn ihre Ableitung f "(x) nichtnegativ ist:
f "(x) = 2ex
Das ist der Fall:
f "(x) = 2ex ≥ 0,
also ist f(x) konvex. (Damit kann das Newton-Verfahren mit x0 = 1 starten.)