Rike hat schon gemerkt, dass ihre zufällige Anordnung von 6 Blumen pro Quadratmeter Charly in der IGA-Aufgabe nicht gefallen hat, ja, dass diese Lösung nicht nur Charly nicht gefällt sondern auch auf der IGA 2017 keinen Beifall gefunden hätte. So überlegt sie, ob es nicht doch eine seriöse Lösung gibt. Sie erinnert sich, dass Gärtner häufig diagonale Anordnungen benutzen. Eine Diagonale ergäbe so ein 5er Muster. Weiterlesen
Kategorie: diskret

AI-generierte Bilder III: Variationen
Rike ist nicht ganz glücklich über die DALL.E-Ergebnisse zu ihrem Bild mit Sinus- und Kosinusfunktionen, die ein Orthonormalsystem für 2π-periodische Funktionen bilden. Sie hatte sich gedacht, dass die „Künstliche Intelligenz“ intelligent ist und die speziellen Funktionen erkennt. Sie wird immer wütender je länger sie darüber nachdenkt.

AI-generierte Bilder II: Diffusionsmodell
Nachdem das Erzeugen von fotorealistischen Bildern mit konkreten Vorgaben mittels AI so schief gelaufen ist, hat Rike eine andere Teststrategie. Sie will testen, wie intelligent die „Künstliche Intelligenz“ wirklich ist. So viele intelligente Algorithmen, so viel Mathematik, was versteht die „Künstliche Intelligenz“ wirklich von Mathematik? So gibt sie probeweise ihr „altes“ Bild von einigen Sinus- und Kosinus-Funktionen ein. Diese bilden ein Orthonormalsystem, gerade das hat sie damals Ben erklärt. Die Darstellung von 2π-periodischen, quadratisch integrierbaren Funktionen als Summe von solchen Schwingungen heißt Fourier-Reihe. Das ist ein wichtiges mathematisches Konzept, in Funktionen Schwingungen zu finden und zu benutzen. Es hat viele technische Anwendungen. Rike fragt sich, ob DALL.E diese Schwingungen erkennen und intelligent variieren kann. Weiterlesen

Große Zahlen in Python
Paula hatte mit Rike das Verschlüsseln mit dem RSA-Verfahren programmiert. Sie haben das flaubertsche Wort erection verschlüsselt und nrtciiie erhalten. Dazu mussten sie die Aufgabe
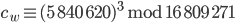
lösen. Die Berechnung hat weniger als 1 s gedauert. Doch viel aufwendiger ist die Dechiffrierung. Das wollen sie heute tun.
Weiterlesen

Flaubert und Python
Rike fühlt sich wohl bei ihrer Schwester. Beide haben in München schon Einiges unternommen: Paula hat Rike den Campus in Garching gezeigt, beide haben Ragnar Axelssons Fotos bewundert, Rike war einmal bei einer Teambesprechung zu einem Game-Konzept dabei, abends haben sie die neusten Spiele gespielt... Für kurze Zeit vergessen sie ihre Sorgen: die steigenden Lebenshaltungskosten, der Krieg in der Ukraine, Zukunftsängste. Eigentlich wollte Rike niemals wieder eine mathematische Aufgabe lösen, doch mit Paula zusammen macht ihr das Diskutieren von mathematischen und Programmier-Themen wieder Spaß. Heute Abend wollen sie ihren RSA-Algorithmus fortsetzen.
Weiterlesen

Mathematische Erektionen
Paula und Rike haben einen schönen Tag in München verbracht. Sie wollen gern den RSA-Algorithmus nach Buchmann in Python implementieren. Doch welchen Text sollen sie nehmen?
Weiterlesen

Paulas merkwürdige Sägezahnkurve
Rike hat 2 Schwestern: Jule und Paula. Beide sind sehr Informatik-affin. Paula studiert Games Engineering. Als Schülerin hatte sie Effi Briest mathematisch analysiert – mit Rikes Hilfe. Nun treffen sich beide in München und diskutieren eine spezielle Kurve im Zusammenhang mit dem RSA-Algorithmus. Weiterlesen

Clusterbildung in Restklassen
Ben und Rike haben ein Programm zur Bestimmung von Zerlegungen von Zahlen N als Summen erstellt. Diese Zerlegungen wurden indiziert – von 1 bis nump. Zu jeder Zerlegung haben sie den dysonschen Rang m modulo q berechnet. Für bestimmte Zahlen N erhält man dann gleichgroße Restklassen von Zerlegungen. Doch wie sind die Indizes verteilt? Sind sie gleichverteilt und sehr zufällig, wie Dyson vermutete oder bilden sich Cluster?
Weiterlesen

Das 2-Farben-Problem für pythagoreische Tripel
Ben und Rike sind wieder am Nordseestrand. Heute erzählt Ben, womit er sich im Urlaub beschäftigen möchte: Er möchte endlich den Beweis von Heule et al. über die Färbung in 2 Farben der pythagoreischen Tripel in Ruhe durchgehen. Der Beweis verläuft computerunterstützt und hatte 2016 für großes Aufsehen gesorgt. Die Aufgabe geht so: Alle natürlichen Zahlen von 1 bis N werden als Kästchen gezeichnet. Diese Kästchen sollen mit 2 Farben so gefärbt werden, dass die pythagoreischen Tripel nicht einfarbig bleiben. Weiterlesen
Wie Lila eine rekursive Folge untersucht
Lila und Max sind in Berlin zusammen. Lilas Mathestudium ist gerade in der Corona-Phase, d.h. sie ist viel zu Hause. Eines Abends erzählt sie Max von den guten alten Präsenzveranstaltungen im Wintersemester mit den wöchentlichen Übungsaufgaben.
Lila Ganz am Anfang hatten wir in Analysis bei Kubicki die Aufgabe, die Folge
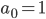
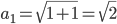
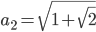

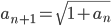
zu untersuchen. Da habe ich ein paar Werte ausgerechnet und gezeichnet. Weiterlesen
