Lila und Max sind in Berlin zusammen. Lilas Mathestudium ist gerade in der Corona-Phase, d.h. sie ist viel zu Hause. Eines Abends erzählt sie Max von den guten alten Präsenzveranstaltungen im Wintersemester mit den wöchentlichen Übungsaufgaben.
Lila Ganz am Anfang hatten wir in Analysis bei Kubicki die Aufgabe, die Folge
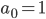
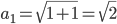
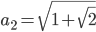

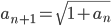
zu untersuchen. Da habe ich ein paar Werte ausgerechnet und gezeichnet.
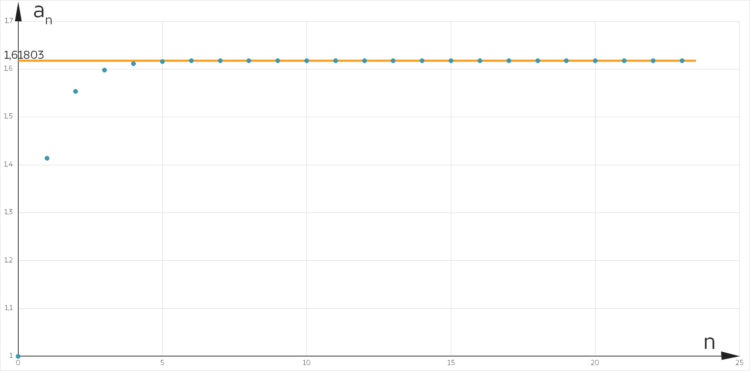
Eigenschaften der Folge (an)
Du siehst, dass die Folge zu 1,61803 geht.
Max Klar!
Lila Aber die Berechnung der ersten Werte reicht nicht! Zumindest nicht für Mathematiker.
Max Haha.
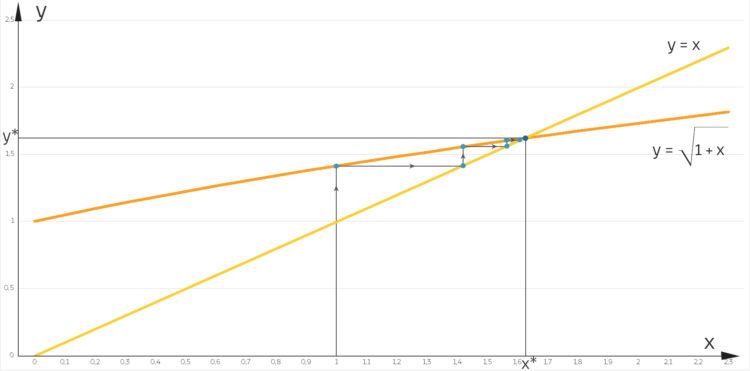
Lila Man kann sich überlegen, dass der Grenzwert im Schnittpunkt der beiden Kurven
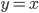
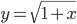
liegt ….
Max Was???
Lila Du betrachtest ganz einfach die Vorschrift der Folge in einem x-y-Koordinatensystem. Du berechnest
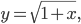
wie eine Funktion
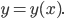
Dann nimmst du das erhaltene y für das nächste x, also
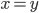
usw.
Max Verstehe.
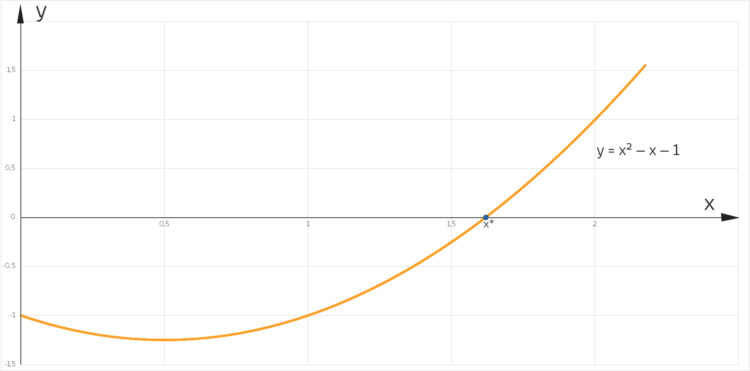
Lila Für den Schnittpunkt der beiden Kurven ergibt sich,
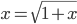
und daraus
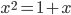
Max Ich weiß, die p-q-Formel!
Lila Stimmt, du kriegst damit heraus, dass die Folge an zu
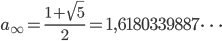
konvergiert. Aber wie könnte ich das beweisen? Klar, schneiden sich die beiden Kurven in dem Grenzwert x*, aber es gab kein allgemeines Bildungsgesetz für jedes Folgenglied an, es gab nur für jede folgende Zahl an+1 eine Formel, um sie aus an zu berechnen, eben rekursiv. Aber könnte die Folge (an) nicht auch über den Punkt x* hinausgehen und doch nicht konvergieren? Wie soll ich das berechnen, wenn ich immer nur von einem zum nächsten komme? Ich sitze ewig dran? So bin ich einfach nicht weitergekommen. Dann ist mir der Zusammenhang eingefallen, aus dem die Aufgabe kam, das war die vollständige Induktion. Das geht so:
Vollständige Induktion im Allgemeinen
Wenn du eine Eigenschaft E für alle natürlichen Zahlen n zeigen möchtest,
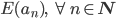
also für unendlich viele an’s, dann muss du diese Eigenschaft für die erste Zahl zeigen:
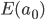
muss richtig sein.
Dann sagst du: Die Eigenschaft E soll für alle an, n ∈ N, n ≤ k gelten:
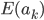
Nun zeigst du, dass dann die Eigenschaft E für ak+1 auch gilt:
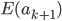
Wenn du das schaffst, ist sie für alle n ∈ N, also für alle natürlichen Zahlen richtig.
Max Aha?!
Vollständige Induktion im Speziellen
Lila Ja, bei dieser Folge (an) könnten wir mal behaupten:
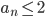
soll für alle n ∈ N gelten. Wir fangen an:
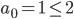
ist richtig. Dann soll
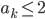
für alle n ≤ k gelten, für irgendein k ∈ N. Jetzt rechnen wir aus, dass
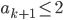
ist. Das ist nicht schwer, denn ist nach dem Bildungsgesetz der Folge (an) ist
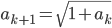
Weil nun aber nach unserer Induktions-Voraussetzung
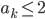
ist, kriegen wir für das ak+1²:
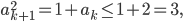
also
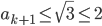
Damit sind alle
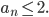
Das ist eine sehr formale Beweismethode, diese vollständige Induktion. Ohne zu zeigen, dass alle
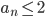
sind, sondern das nur für n = 1 zu zeigen und den Rest für ak zu behaupten und mit der Behauptung die Eigenschaft für ak+1 zu zeigen, kommt man auf die Lösung. Tatsächlich habe ich nur das Bildungsgesetz und
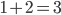
benutzt. Das ist ja elementar.
Konvergenz der Folge
Max Aha.
Lila Außerdem zeigt man, dass die Folge (an) monoton wächst:
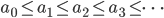
und weil sie von oben durch 2 beschränkt ist, wie du jetzt weisst, konvergiert die Folge.
Als ich die Lösung für diese Übungsaufgabe aufgeschrieben hatte, habe ich mich richtig gut gefühlt, ich war stolz auf mich.
Max Ich verstehe es zwar nicht ganz, es ist wie Zauberei, aber wenigsten liefert
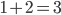
einen bedeutenden Beitrag zur höheren Mathematik.
Lila Haha.
***
Übungsaufgabe
Zeige, dass die Folge (an) mit an ∈ (0, x*] monoton wächst.
Lösung
Für 2 reelle, nichtnegative Zahlen a und b mit
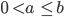
ist nach den Axiomen bzw. Rechenregeln für Ungleichungen
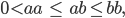
also
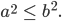
Das heißt, wir können Ungleichungen quadrieren. Wegen
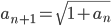
ist dann
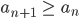
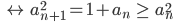
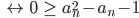
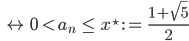
Also ist für alle an ∈ (0, x*] (ak) monoton wachsend.