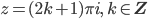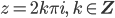Charly, der Mathe- und Sportlehrer von Finja, Justin und Fabian ist zu Hause und bereitet die nächsten Hausaufgaben für seine Schüler und Schülerinnen vor. Dabei fällt ihm die eine Aufgabe aus dem Mathebuch auf:
Begründen Sie.
a) Die Gleichunghat keine Lösung.
b) …
Die reelle e-Funktion
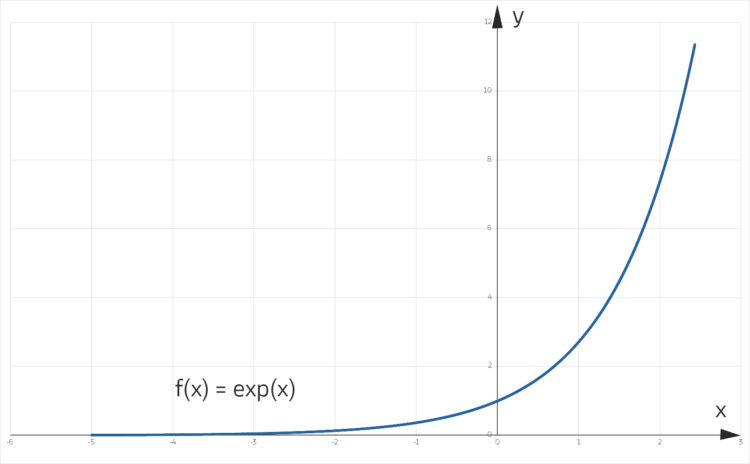
Einerseits ist die Aufgabe trivial, wenn die Kinder erst mal für die e-Funktion im Reellen
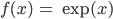
die Berechnungsvorschrift kennengelernt haben und die Funktion gezeichnet haben:
Es ist nämlich
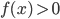
für alle reellen x. Andererseits lässt es sein Credo nicht zu, dass die Kinder lernen, dass

keine Lösung hat. Er regt sich ziemlich darüber auf und ruft nach langer Zeit mal wieder Rike an. Die kennt sich ja so gut mit komplexen Zahlen aus.
Charly Hallo, Rike, wie geht es dir? Alles im Lot?
Rike Hallo, Charly, wie geht es dir?
Charly Rike, ich habe ein Problem, ein Mathe-Problem. In meinem Lehrbuch gibt es eine Aufgabe über den Nachweis, dass ex niemals -1 werden kann.
Rike Das kann nicht war sein? Kennen denn die Autoren gar nicht die Eulerformel?
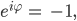
diese geniale Sache von Euler, wo die komplexen Zahlen Anwendung finden, das 1, e und π nebeneinander in Beziehung stehen? Ohne die Formel gibt es keine Quantentheorie, keine Zeta-Funktion, keine Elektrotechnik! Ich fasse es nicht! Das ist wirklich eine Tragödie!
Charly Und was soll ich tun? Soll ich sagen, das ist wirklich eine Tragödie?
Rike Weißt du, du bietest einfach eine schöne Herleitung anstelle der Aufgabe!
Charly Und wie geht die Herleitung?
Rike Was habt ihr denn bis jetzt besprochen?
Die e-Funktion als Lösung einer DGL
Charly Dass die e-Funktion mit ihrer Ableitung übereinstimmt!
Rike Na, dann greif das doch auf! Es ist:
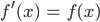
Das heißt, die e-Funktion
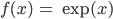
ist die Lösung dieser Differentialgleichung mit dem Anfangswert
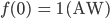
Charly Okay, eine ganz andere Sichtweise – ja, das ist gut!
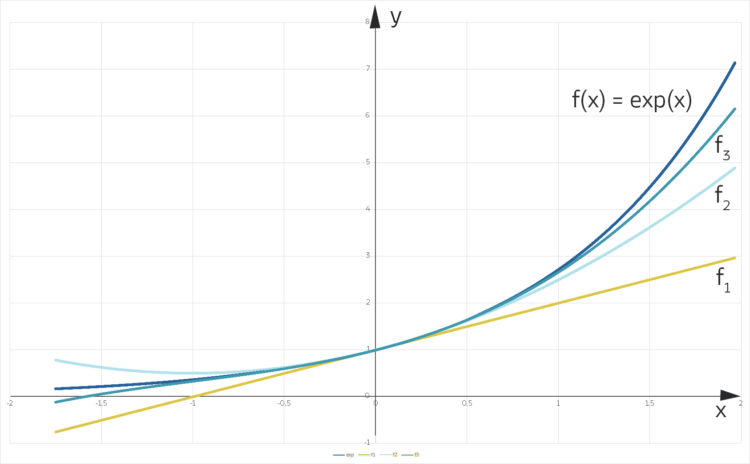
Die Näherung der e-Funktion
Rike Du kannst die Ableitung an der Stelle x = 0 ausrechnen und die e-Funktion an dieser Stelle gut linear nähern
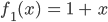
und das kannst du natürlich auch mit der 2. Ableitung und der Näherung 2. Grades machen:
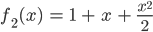
und immer so weiter:
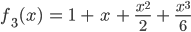
So kommst du auf die Reihe:
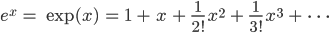
Für die Sinus- und Kosinus-Funktion kann man das ebenso machen und erhält sehr ähnliche Reihen, die ihr in jeder Formelsammlung findet:
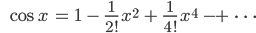
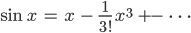
Charly Okay!
Die komplexe e-Funktion
Rike Dann hat Euler vorgeschlagen, die Reihen auch für komplexe Zahlen z zu benutzen:
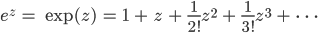
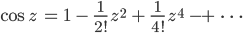
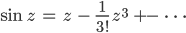
Setzt du dann
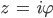
in die Reihen ein, dann erhältst du
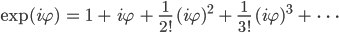
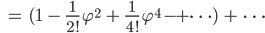
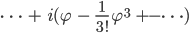
Charly Krass!
Die Eulerformel
Rike Ja, echt krass. Daraus erhälst du schließlich die berühmte Eulerformel
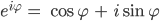
Im Spezialfall
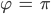
kriegst du die Formel
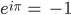
Da hast du deine Hausaufgabe!
Charly Okay, Rike, danke dir! Da steckt ja so viel dahinter! Ich versuche es! Ja, die Eulerformel ist zumutbar.
***
Übungsaufgaben
- Gibt es noch weitere Lösungen von ez = -1, z ∈ Z?
- Löse ez = +1 für z ∈ Z.
Lösungen