Exponentielles Buchenwachstum

Justin und sein Vater sind nun mit ihrer Gartenarbeit fertig. Sie haben einen Baum gepflanzt und den Zaun repariert. Jetzt geht Justin wieder an seine Matheaufgaben. Unter dem Stichpunkt exponentielles Wachstum mit der e-Funktion wird in einer Aufgabe das Wachstum von Buchen modelliert. So soll der Durchmesser d einer Rotbuche in den ersten 75 Jahren nach dem Gesetz

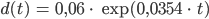
wachsen, t ist die Zeit in Jahren. Die Aufgabe besteht darin, zu einem Durchmesser das Alter herauszufinden.

Exponentielles Wachstum

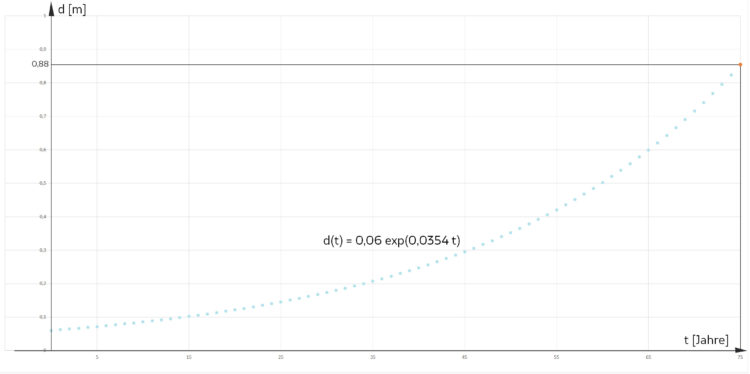
Er fragt sich, wie es denn nach 75 Jahren weitergeht. Er hat gelesen, dass Buchen 300 Jahre alt werden. Wenn er die Funktion d einfach fortsetzt bis t = 300, hat er ein riesiges Wachstum:

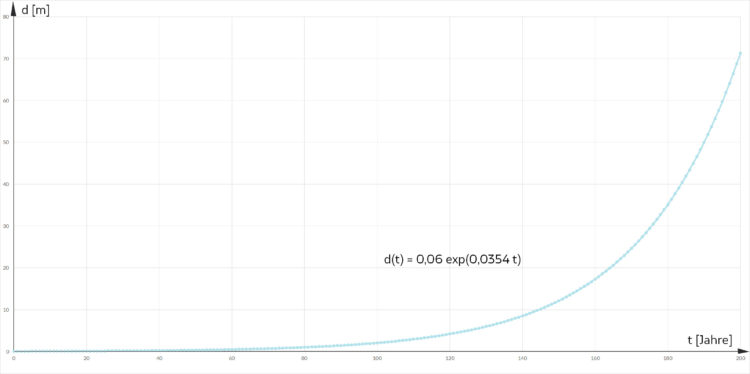
Nach 300 Jahren wäre der Durchmesser fast 2,5 km!

Stückweises exponentielles Wachstum

Also überlegt er, ob er die Funktion d ab t = 75 durch eine andere Exponentialfunktion fortsetzt

für

für

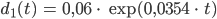
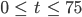
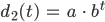
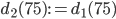
A: Stetig differenzierbare Forsetzung

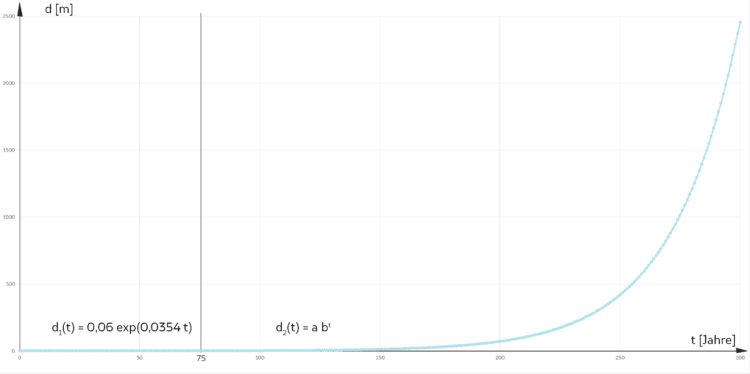
Er hofft, ein langsameres Wachstum zu erhalten. Weil aber das Wachstum so gleichmäßig verläuft und im Jahre 75 gar nichts Besonderes ist, nimmt er als 2. Bedingung, dass der Anstieg der Funktion an der Stelle t = 75 gleich der ursprünglichen ist:

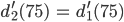
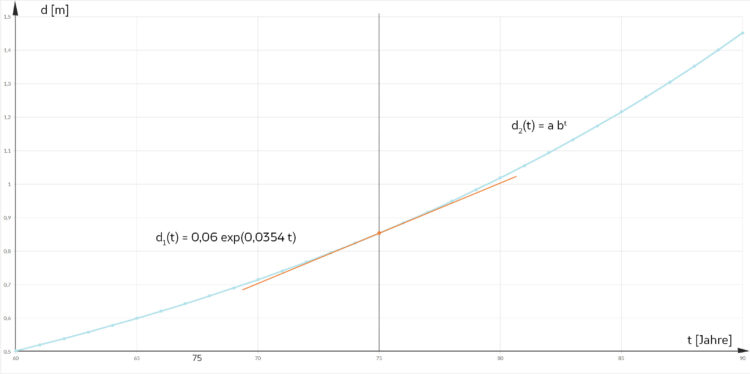
Doch er wundert sich, als er die so schön fortgesetzte Funktion zeichnet, nach 300 Jahre hätte die Buche wieder einen Durchmesser von fast 2,5 km erreicht. Da ruft er Finja an und erzählt ihr das Problem.

Justin Hi, Finja, ich rufe wegen der Buchenaufgabe an. Ich war eine Woche mit meinem Vater im Garten! Ich habe das Gras und die Bäume wachsen sehen!

Finja Hi, Justin, lange nichts von dir gehört! Jetzt verstehe ich! War ja schönes Wetter!

Justin Ja, das Wetter war klasse. Dann habe ich die Buchenaufgabe gemacht und wollte die Funktion fortsetzen: durch eine andere Exponentialfunktion, die langsamer wächst. Ich habe einen Ansatz gemacht und an der Stelle t = 75 die Funktion stetig differenzierbar fortgesetzt. Ich habe dieselbe Funktion herausbekommen! So ein Mist! Nach 300 Jahren hätte sie einen Durchmesser von 2,5 km.

B: Stetige Fortsetzung mit Randbedingung

Finja Haha! Wie dick soll sie denn eigentlich werden?

Justin Bei Wikipedia steht, ca. 2 m!

Finja Dann lass uns doch wieder deinen Ansatz

für

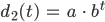
nehmen. Natürlich brauchen wir die stetige Fortsetzung:

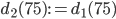
und als Randbedingung nehmen wir

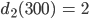
Justin Okay. Warte ich bestimme mal a und b …

Dann kriege ich

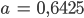
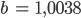
und die Kurve kann ich auch zeichnen:

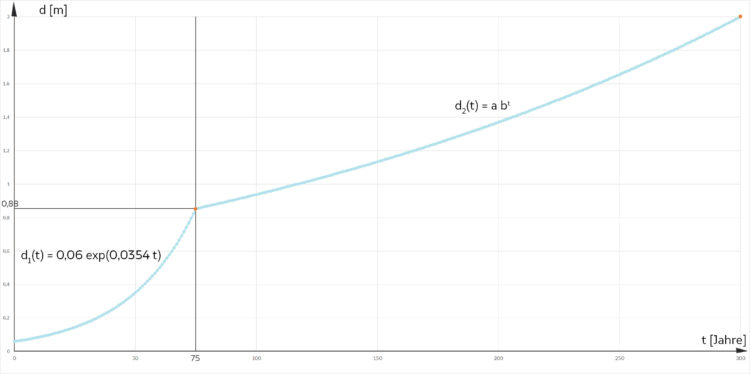
Fazit

Na! Ich glaube, Buchen wachsen nicht so! So ein Knick bei 75 Jahren! Als wäre etwas Schlimmes passiert!

Finja Haha, vielleicht wachsen Buchen doch nicht exponentiell?

***

Übungsaufgaben

1. Warum hat Justin dieselbe Funktion herausbekommen?
2. Modelliere besser!

Lösungen

1. Die Funktion

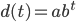
   lässt sich auch als e-Funktion schreiben:

   und wird durch a und b vollständig bestimmt, zB

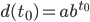
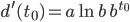
   Das Verhältnis beider lässt sich gut nach b auflösen:

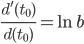
   Dh, jede Exponentialfunktion ist durch einen Funktionswert und den Anstieg an derselben Stelle vollständig bestimmt.

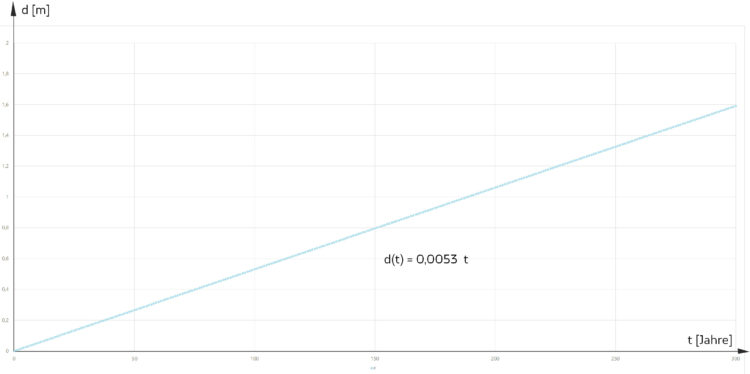
2. Im Gartenjournal wird eine Formel für das Buchenwachstum angegeben, es ist linear.