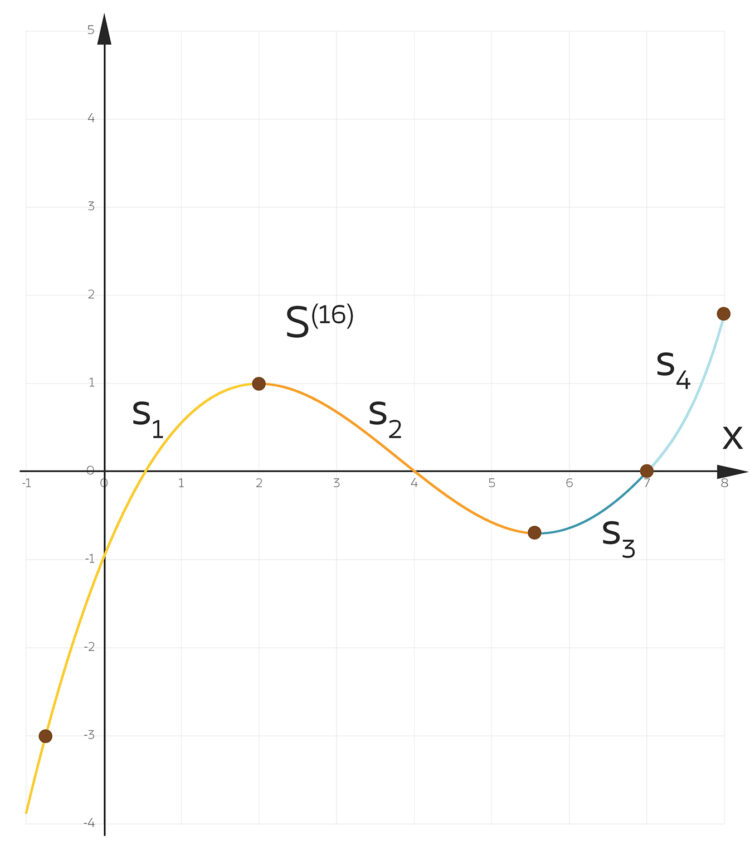
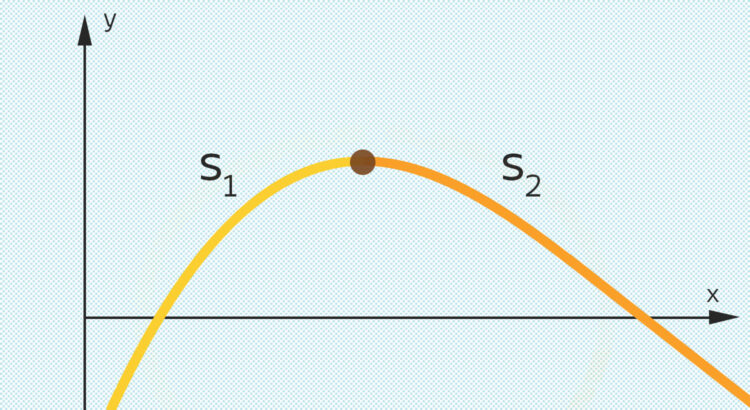
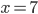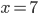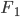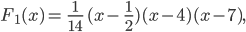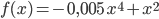Rike hat lange über Newtons Vorwürfe nachgedacht: Sie spinnt jawohl mit ihrer Forderung, die 1. Ableitung der Funktion f(y) an der ersten Näherung y0 soll ungleich Null sein:
f(y0) ≠ 0,
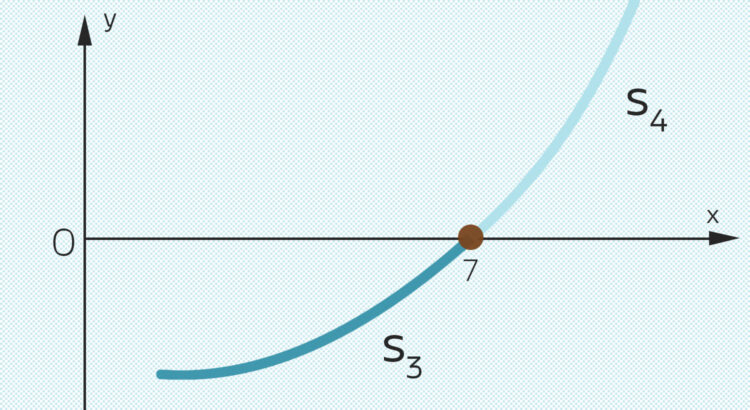
hat Newton gerufen. Das ist doch Standard bei diesem Verfahren und geometrisch offensichtlich. Eine waagerechte Tangente kann keinen Schnittpunkt mit der y-Achse haben.
Als Charly mit seiner Klasse in ein Volleyball-Trainingslager fährt, färbt sie sich die Haare silbergrau, deckt sich mit Chips und Cola ein und sucht Newtons Original. Bloß gut, dass die University of Cambridge Newtons Arbeiten digitalisiert und online gestellt hat! Sie sieht fast die gesamte Abhandlung Fluxes durch, das ist Newtons Darstellung der Differential- und Integralrechnung, und findet schließlich nach einem Hinweis von Wiki das Papier:
Weiterlesen