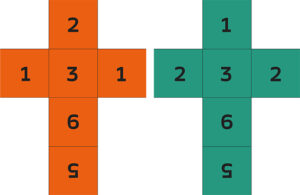
Charly möchte gerne die Wahrscheinlichkeiten der rot-grünen Würfelaufgaben e) und f) überprüfen, ohne wirklich jemanden würfeln zu lassen. Mit den speziellen roten bzw. grünen Würfeln, die an der Stelle der 4 eine 1 bzw. eine 2 haben. Die Anordnung der Zahlen auf dem Würfel entspricht nicht den Standard-Würfeln, doch das macht nichts, denn jede Seite ist gleichberechtigt.
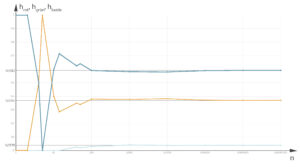
Jeder der beiden Spieler würfelt dreimal. Wer die Augensumme 6 erwürfelt, gewinnt. Die Wahrscheinlichkeit, dass der Spieler mit dem grünen Würfel die Augensumme 6 erwürfelt, ist 9.26 %, für die Spielerin mit dem roten Würfel ist sie 5.46 %. Also wird vermutlich keiner gewinnen. Charly hat die Aufgabe abgeändert: Wenn keiner die Augensumme 6 erhält, würfeln beide erneut, bis jemand oder beide gleichzeitig die 6 erhält. Die Wahrscheinlichkeit, dass irgendwann Grün gewinnt, ist 59,12 %, für Rot ist sie bei 37,10 % und für beide ist sie 3.78 %, siehe letzter Beitrag.
Charlys Wunsch, das Ergebnis zu testen
Charly Sag mal, Rike, mit einem Tabellenkalkulationsprogramm kann ich zwar Zufallszahlen erzeugen und beide Spieler imitieren, aber doch nur per Hand und nur wenige Spiele. Kannst Du das nicht in Python simulieren und programmieren?
Rike Glaubst du das Ergebnis nicht? Dieser Ansatz entstand aus den Verhältnissen der Wahrscheinlichkeiten für das Würfeln einer 6 und der linearen Gleichung, die daraus entstand… – ist das nicht toll?
Charly Hmm, ja, ein bisschen akademisch würde ich sagen, schwer zu vermitteln, ich würde das einfach mal überprüfen wollen.
Rike Okay. Weißt du, ich kann das programmieren, doch jedes Mal kommt etwas anderes 'raus.
Charly Aber wenn wir sehr viele Spiele simulieren, dann konvergiert die Häufigkeit des Gewinnens doch gegen die berechnete Wahrscheinlichkeit.
Konvergenz von Zahlenfolgen
Rike Ganz so einfach ist das nicht, Charly. Wenn eine Zahlenfolge 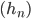 gegen einen Grenzwert
gegen einen Grenzwert 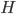 strebt,
strebt,
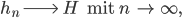
dann muss für jedes noch so kleine 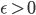 eine Zahl
eine Zahl  existieren, sodass
existieren, sodass
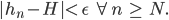
D.h. die Folge 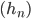 geht immer näher an den Grenzwert
geht immer näher an den Grenzwert 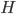 heran.
heran.
Charly Klar, verstehe, bei den Häufigkeiten doch auch.
Rike Nein, hier ist das anders, wir haben hier Häufigkeiten von zufälligen Ereignissen, die Ergebnisse sind nicht deterministisch. Es kann passieren, dass trotz der geringen Wahrscheinlichkeit, die Augenzahl 6 zu würfeln, beide mehrfach hintereinander gewinnen. Dann kommen die Häufigkeiten dem Grenzwert nicht mehr beliebig nahe und die Konvergenzbedingung ist nicht für alle Versuche  erfüllt.
erfüllt.
Charly Aber das ist sehr, sehr unwahrscheinlich!
Gesetz der großen Zahlen
Rike Genau! Das ist es. Es gibt verschiedene Versionen des Gesetzes der großen Zahlen, eine wäre der Satz von Bernoulli, der geht so: Wir haben eine Zufallsgröße 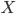 für das Eintreten eines Ereignisses. Jeder Versuch ist unabhängig, die Wahrscheinlichkeit des Eintretens des Ereignisses
für das Eintreten eines Ereignisses. Jeder Versuch ist unabhängig, die Wahrscheinlichkeit des Eintretens des Ereignisses 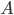 sei
sei 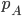 ,
,  ist die Anzahl der Versuche und
ist die Anzahl der Versuche und 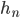 ist die Anzahl des Eintretens von
ist die Anzahl des Eintretens von 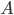 in
in  Versuchen. Dann ist für jedes
Versuchen. Dann ist für jedes 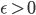
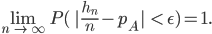
Charly O Gott, was bedeutet das?
Rike Das ist eine schwache Konvergenz. Sie sagt, dass die Wahrscheinlichkeit, dass die relative Häufigkeit 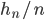 gegen
gegen 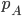 strebt, nach 1 strebt. Dass es sehr unwahrscheinlich ist, dass beide mehrfach hintereinander gewinnen.
strebt, nach 1 strebt. Dass es sehr unwahrscheinlich ist, dass beide mehrfach hintereinander gewinnen.
Charly Okay, etwas umständlich ausgedrückt. Aber beim Sport ist es eigentlich genauso. Wir können beim Volleyball die besten Spielerinnen haben, in der Tabelle weit oben stehen und sollten eigentlich jedes Spiel gewinnen, doch manchmal klappt das nicht.
Rike Haha, wie im echten Leben.
Charly Kannst du dann also dennoch ein solches Programm schreiben und wir testen dann die „schwache Konvergenz“? Ist das schwer?
Rike Okay, ich glaube, es ist nicht schwer, es geht straight forward. Durch Zufallszahlen von 1 bis 6 imitieren wir die Würfel. Beim roten Würfel ersetzen wir eine gewürfelte 4 durch eine 1, beim grünen Würfel die 4 durch eine 2. Wir lassen beide dreimal würfeln, zählen die Augenzahl und überprüfen, ob 6 erreicht wurde. Wenn nicht, würfeln die beiden wieder, so lange, bis einer, eine oder beide eine 6 haben. Das merken wir uns, die Anzahl der Gewinne für jeden und beide. Darüber machen wir eine Schleife und lassen die beiden spielen, solange du willst.
Rikes Programmablaufplan
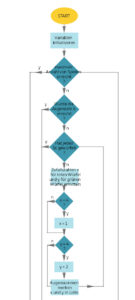
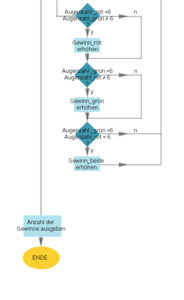 Charly Ja, das ist gut, solange ich will. Dein Plan hört sich so einfach an.
Charly Ja, das ist gut, solange ich will. Dein Plan hört sich so einfach an.
Rike Ist er auch.
***
Übungsaufgaben
- Programmiere die rot-grüne Würfelaufgabe.
- Vergleiche die relativen Häufigkeiten.
Lösung
1. 10_2022_wuerfelaufgabe_python_08.pdf
2.