Newtons Original und Rikes Anwendung

Rike hat lange über Newtons Vorwürfe nachgedacht: Sie spinnt jawohl mit ihrer Forderung, die 1. Ableitung der Funktion f(y) an der ersten Näherung y₀ soll ungleich Null sein:

f(y₀) ≠ 0,

hat Newton gerufen. Das ist doch Standard bei diesem Verfahren und geometrisch offensichtlich. Eine waagerechte Tangente kann keinen Schnittpunkt mit der y-Achse haben.

Als Charly mit seiner Klasse in ein Volleyball-Trainingslager fährt, färbt sie sich die Haare silbergrau, deckt sich mit Chips und Cola ein und sucht Newtons Original. Bloß gut, dass die University of Cambridge Newtons Arbeiten digitalisiert und online gestellt hat! Sie sieht fast die gesamte Abhandlung Fluxes durch, das ist Newtons Darstellung der Differential- und Integralrechnung, und findet schließlich nach einem Hinweis von Wiki das Papier:

Newtons Original zum Newtonverfahren

Newton beschreibt in einer einseitigen Notiz innerhalb seiner Fluxes-Arbeit, wie er näherungsweise die Nullstelle des Polynoms

y³ - 2y – 5 = 0   (1)

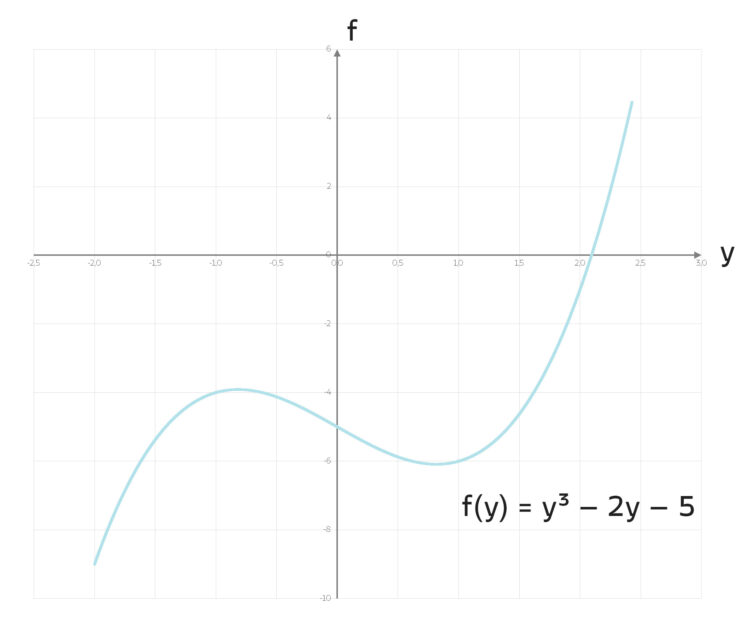
sucht.

Newtons 1. Ansatz

Die Nullstelle liegt nahe bei

y₀ = 2.

Er will sie relativ genau bestimmen, eine Stelle nach dem Komma – so wie in der allerbesten Skipistenaufgabe  – das reicht ihm nicht aus. Er macht den Ansatz für y:

y = 2 + p.    (2)

p ist dann relativ klein. Diesen Ansatz (2) setzt er in die Ausgangsgleichung (1) ein und erhält die Gleichung

p³ + 6p² + 10p – 1 = 0.    (3)

Hier lässt er die quadratischen und kubischen Terme weg, weil ja p sehr klein ist. Dann bleibt nur noch die lineare Gleichung

10p – 1 = 0

zu lösen:

p = 0.1.

So verbessert er die Genauigkeit. Statt

y₀ = 2

findet er die neue Näherung

y₁ = 2.1.

Jetzt macht er genauso weiter.

Newtons 2. Ansatz

Mit dem 2. Ansatz für p:

p = 0.1 + q    (4)

erhält Newton nach Einsetzen in die Gleichung (3) die folgende neue Gleichung:

q³ + 6.3q² + 11.23q + 0.061 = 0.    (5)

In (5) lässt er wieder kubische und quadratische Terme weg:

11.23q + 0.01 = 0. (6)

Die Lösung von (6) ist

q = –0.0054.

Damit verbessert er seine Näherung der Nullstelle nochmals und erhält

y₂ = 2.0946

Newtons 3. Ansatz

Mit dem nächsten Ansatz für q:

q = –0.0054 + r    (7)

will er die Näherung noch genauer machen und setzt den Term (7) in die Gleichung (5) ein. Genau wie Rike in seiner Arbeit lesen kann, erhält er schließlich die lineare Gleichung

0.0005416 + 11.23r = 0

und kann die nach r auflösen:

r = –0.00004852.

Damit erhält er seine dritte Näherung:

y₃ = 2.09455148.

Newton notiert den nächsten Ansatz. Rike denkt, die Genauigkeit sollte dann reichen. Aber was ergibt das eigentliche Newtonverfahren?

Das Newtonverfahren für Newtons Polynom

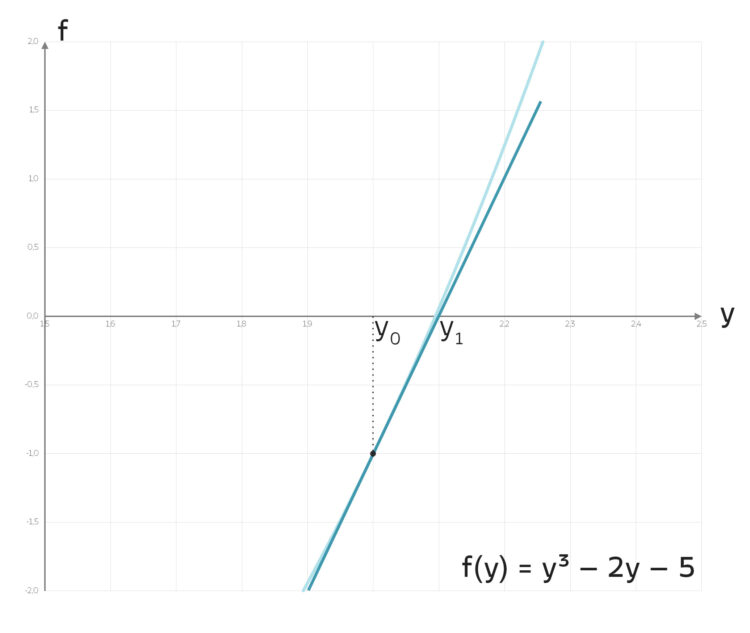
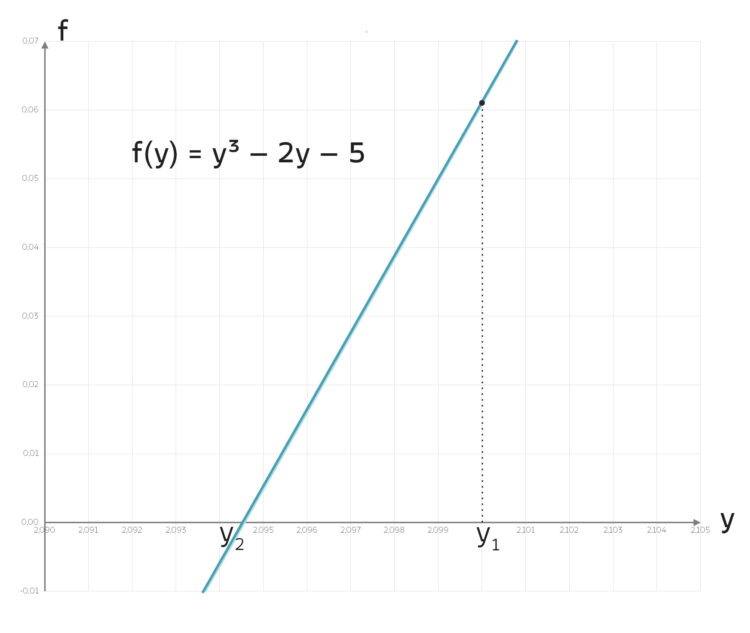
Rike freut sich. Sie erhält genau dieselben Ergebnisse mit der Vorschrift

Sie wundert sich, dass Newton keine Zeichnung gemacht hat, keine Tangente angelegt hat und auch nicht die Vorschrift des Newtonverfahrens benutzt hat, wohl aber die Bedingung, dass der Startwert y₀ nahe der Nullstelle liegt.

Rikes Beispiel

Rike sucht nun ein Beispiel eines Polynoms f₁(y) mit reellen Nullstellen. Sie möchte einen Startwert y₀ wählen, der wie bei Newton mindestens bis auf eine Stelle nach dem Komma nahe einer Nullstelle liegt, aber eine verschwindende 1. Ableitung hat:

f₁'(y₀) = 0.

Wie funktioniert dann Newtons originale Idee mit den Ansätzen?

Sie findet das Polynom

f₁(y) = y³ + 2.5y² + 2.06y + 0.56.

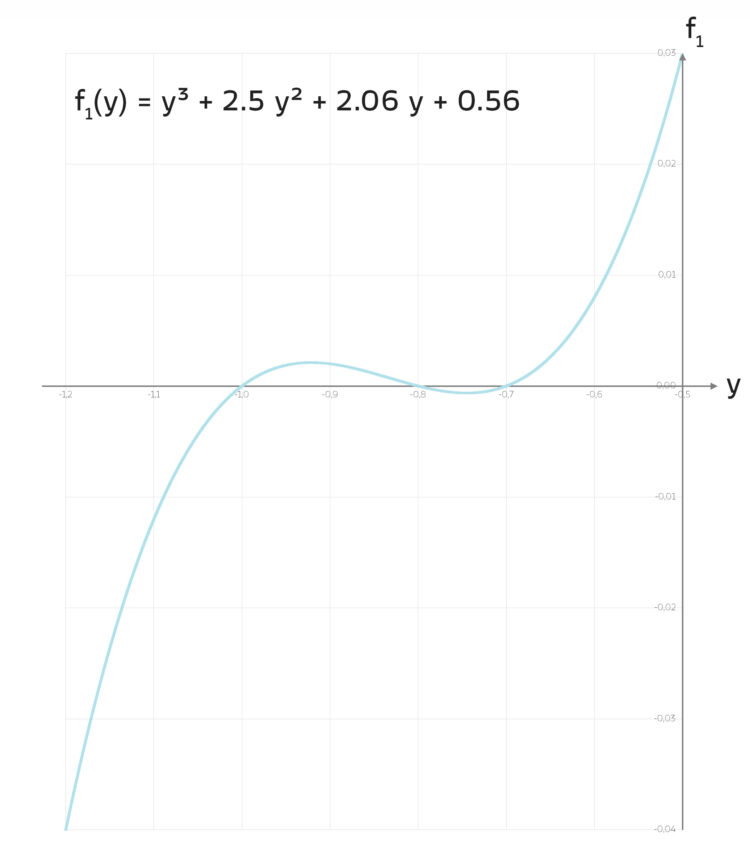
Es hat zwei Stellen y mit waagerechter Tangente.

Rikes Anwendung der newtonschen Originalmethode

Sie wählt einen davon als Startwert:

y₀ = –0.7451416   (8)

Dann macht sie den newtonschen Ansatz

y = y₀ + p

= –0.7451416 + p.   (9)

Sie setzt diesen Ausdruck (9) in

f₁(y) = y³ + 2.5y² + 2.06y + 0.56 = 0    (10)

ein. Nach einiger Rechnerei stellt sie befriedigt fest, dass der lineare Term entfällt, die neue Gleichung heißt:

p³ + 0.264575131p² – 0.0006 = 0    (11)

Newton hatte die kubischen und quadratischen Terme weggelassen und eine lineare Gleichung erhalten, die gut zu lösen war. Jetzt hat sie aus einer Gleichung 3. Grades eine neue Gleichung 3. Grades erhalten! Das ist ja toll! Sie denkt darüber nach und merkt, dass sie viel zu analytisch herangeht. Sie will ja nur eine Näherungslösung haben. Was würde Newton machen?

Die 1. newtonsche Idee

Newton würde das Absolutglied in (11) weglassen, es ist in er Größenordnung von 10^-4, das ist wirklich sehr klein:

p³ + 0.264575131p² = 0     (12)

Das ergibt zwar wieder eine kubische Gleichung, die aber leicht aufzulösen ist:

p² ∙ (p + 0.264575131) = 0.

Die einzige nichttriviale Lösung ist

p₁ = –0.264575131

Daraus erhält Rike ihre erste Näherung y₁⁽¹⁾ zum Startwert y₀:

y₁⁽¹⁾ = y₀ + p₁

= –1.0097

Die 2. newtonsche Idee

Außerdem würde Newton versuchen, den kubischen Teil in (11) wegzulassen:

0.264575131p² – 0.00006 = 0     (13)

So erhält sie die quadratische Gleichung (13), die sie ebenfalls leicht lösen kann:

p_2,3 = ± 0.047621

Aus diesen beiden Näherungslösungen erhält Rike die beiden nächsten Näherungen für die Nullstellen ihres Polynoms f₁(y):

y₁⁽²⁾ = y₀ + p₃

= –0.7927629

und

y₁⁽³⁾ = y₀ + p₂

= –0.6975203.

Fazit

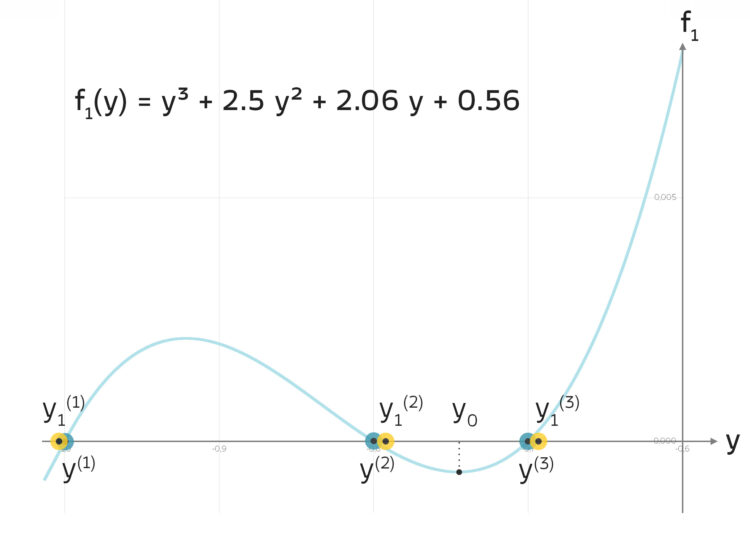
Mit Newtons Ideen hat Rike 3 Näherungslösungen p_i der kubischen Gleichung (11) gefunden. Folglich hat sie auch  3 Näherungslösungen ihres Polynoms f₁(y) gefunden. Sie startete mit einem Anfangswert y₀, wo das Newtonverfahren normalerweise versagt. Doch welche davon sind brauchbar?

Sie sieht, dass alle 3 Näherungen y₁⁽ⁱ⁾ sehr gute Näherungen für die Nullstellen sind. Mit dem Newtonverfahren, das einige Zeit nach Newton von Joseph Raphson und Thomas Simpson verallgemeinert wurde und in der Berechnungsvorschrift

"gipfelt", kann Rike nun weiterrechnen. Gottseidank hat das Polynom hier keine waagerechten Tangenten. So kann sie mit wenigen Schritten eine große Genauigkeit für ihre Nullstellen finden, was Newton bestimmt gefallen würde.

Jetzt ruft sie Charly an und berichtet ihm von ihrem Erkenntnisfortschritt.

[Zur Fortsetzung]

***

Übungsaufgaben

1. Welches ist Newtons 4. Ansatz?
2. Nach wie vielen Iterationen für y_i stimmt die 4. Stelle nach dem Komma in Newtons Originalaufgabe?
3. Überprüfe die Rechnung mit dem anderen Startwert

   y₀ = –0.92152504

Lösungen

1. r = –0.00004852 + s
2. nach der 2. Iteration (n = 2)
3. Mit

   y₀ = –0.92152504   (8')

   und dem newtonschen Ansatz

   y = y₀ + p

   = –0.92152504 + p   (9')

   erhält man durch Einsetzen in (10)

   p³ – 0.264575131p² + 0.00211 = 0.    (11')

   Durch Weglassen des Absolutgliedes erhält man die erste Näherung für p:

   p₁ = 0.264575131

   und

   y₁⁽¹⁾ = –0.65695

   Durch Weglassen des kubischen Terms in (11') erhält man zwei weitere Näherungen für p:

   p_2,3 = ± 0.08930

   und schließlich die Näherungen für die Nullstellen des Polynoms (10)

   y₁⁽²⁾ = y₀ + p₃

   = –0.83222

   und

   y₁⁽³⁾ = y₀ + p₂

   = –1.01082.