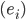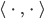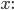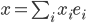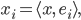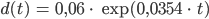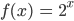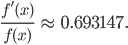Zutaten: Zucker, Kakaomasse (50%), Milchzucker, Weizenmehl, Vollmilchpulver,
Magermilchpulver, Butterreinfett, Sahnepulver, Butter (1,4%)
Kann Spuren von Analysis und Geometrie enthalten.

Rike erzählt Ben wieder von ihren Entdeckungen im Hilbertraum.
Rike Weißt du, diese Hilberträume mit Orthonormalsystemen 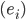 , Skalarprodukt
, Skalarprodukt 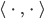 und dem schönen Zerlegungssatz für jeden Vektor
und dem schönen Zerlegungssatz für jeden Vektor 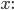
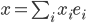
mit
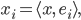
die findest du nicht nur im Zwei- oder Dreidimensionalen. Du als Informatiker hast ja viel mit längeren Arrays zu tun… Weiterlesen

Ben und Rike sitzen zusammen, Rike erzählt eine Geschichte aus ihrem Matheunterricht damals in der Schule.
Die Verzweiflung von Rikes Lehrer
Rike Als ich in die weiterführende Schule kam, hatten wir endlich Geometrie: Punkte, Geraden, Kreise, wir haben Winkel gemessen, Dreiecke gezeichnet usw. Ich erinnere mich noch, als unser Mathelehrer, Herr Wiezorek, uns parallele Geraden erklärte: Weiterlesen

Rike und Ben sind in Urlaub an die deutsche Nordseeküste gefahren. Sie bewundern den weiten Strand. Hier fällt Rike eine Story aus ihrer (mathematischen) Kindheit ein:
Rike Ich war immer von Kreisen fasziniert.
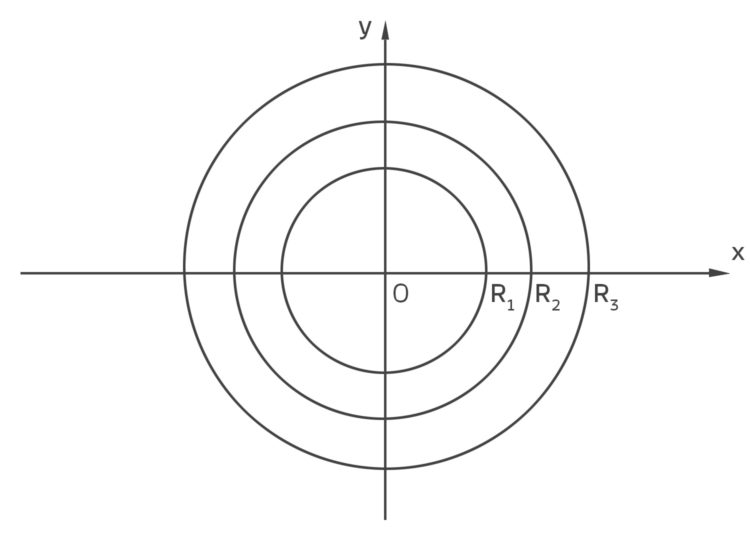 Weiterlesen
Weiterlesen

Justin und sein Vater sind nun mit ihrer Gartenarbeit fertig. Sie haben einen Baum gepflanzt und den Zaun repariert. Jetzt geht Justin wieder an seine Matheaufgaben. Unter dem Stichpunkt exponentielles Wachstum mit der e-Funktion wird in einer Aufgabe das Wachstum von Buchen modelliert. So soll der Durchmesser d einer Rotbuche in den ersten 75 Jahren nach dem Gesetz
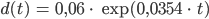
wachsen, t ist die Zeit in Jahren. Die Aufgabe besteht darin, zu einem Durchmesser das Alter herauszufinden. Weiterlesen
Fabian, der praktisch Veranlagte, kämpft sich immer noch allein zu Hause durch seine Aufgaben durch. Er hat nun die Exponentialfunktion
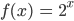
verstanden. Jetzt geht es um die Ableitung der Funktion. Dazu sollen die Schüler und Schülerinnen ihren GTR benutzen und damit die Ableitung dieser Funktion berechnen, um dann die Formel für die „richtige“ Ableitung f‘(x) zu erraten. Die Ableitung und die originale Funktion haben einen Quotienten von
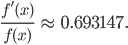
Weiterlesen

Fabian, der praktisch Veranlagte, kämpft sich allein zu Hause durch seine Aufgaben. Er soll die Exponentialfunktion und ihre Ableitung verstehen. In seinem Buch wird die Funktion
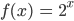
untersucht. Er findet die Wertetabelle ... Weiterlesen

Finja, Justin und Fabian holen den verpassten Unterricht nach, den ihre Mitschüler und Mitschülerinnen in den letzten Wochen zu Hause machen mussten. Auch sie sind jetzt zu Hause. Sie sollen eine Aufgabe unter der Überschrift Wachstumsprozesse mit der e-Funktion beschreiben lösen. Die Aufgabe geht so:
In einem Labor wird das Wachstum einer Insektenpopulation untersucht. Ein Anfangszustand von 38 Insekten nimmt wöchentlich um 16,2 % zu.
a) Beschreiben Sie das Wachstum der Insektenpopulation mithilfe der e-Funktion.
b) …
Weiterlesen

Nun ist es soweit, Charly macht mit einigen seiner Schüler und Schülerinnen eine Expedition nach Kurzras in Südtirol (Italien) nahe der österreichischen Grenze. In den Ötztaler Alpen liegt nämlich der Gletscher Hintereisferner. Sie machen eine geführte Wanderung zum Gletscher und lassen sich von einem Bergführer begleiten. Max ist auch mitgekommen, er fotografiert, filmt und berichtet für eine Berliner Zeitung.
Trotz einiger Schwierigkeiten kommen sie am Hintereisferner an. Die Gruppe bewundert das Tal, das mal vom Gletscher ausgefüllt war. Letzte Woche hat es geschneit und der Gletscher hat etwas zugenommen, sagt der Bergführer. Im Sommer nimmt er wieder ab. Aber wie kann man die Eiszu- oder -abnahme messen? Weiterlesen

Charly ist nun mal in Berlin und heute schafft er es endlich, Rike zu treffen. Sie freuen sich. Rike fragt Charly, wie es ihm geht. Hat er auch schon Abi-Aufgaben betreut? Kennt er die Berliner Aufgaben? Der Tagespiegel hat sie wegen des großen Protestes veröffentlicht. Hier ist die Aufgabe über einen Tunnelbau. Weiterlesen
 zwischen den Kurven
zwischen den Kurven 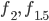 und der
und der  -Achse von knapp 30 m² ausgelegt.
-Achse von knapp 30 m² ausgelegt.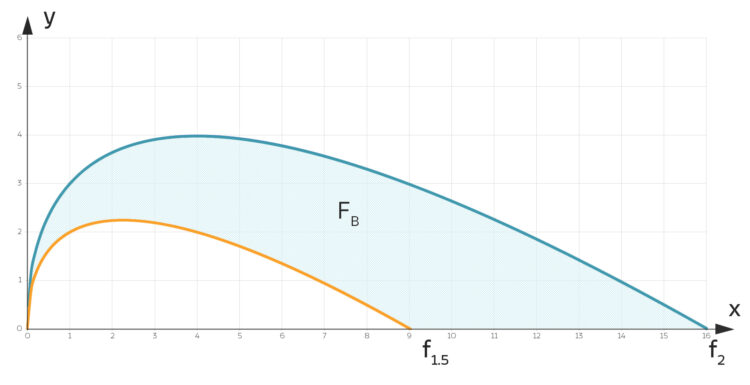
 , die mit Blumen zu belegen ist. Für die Formeln von
, die mit Blumen zu belegen ist. Für die Formeln von 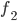 und
und 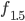 siehe Beitrag Die IGA-Aufgabe.
siehe Beitrag Die IGA-Aufgabe.