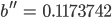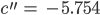Nun ist es soweit, Charly macht mit einigen seiner Schüler und Schülerinnen eine Expedition nach Kurzras in Südtirol (Italien) nahe der österreichischen Grenze. In den Ötztaler Alpen liegt nämlich der Gletscher Hintereisferner. Sie machen eine geführte Wanderung zum Gletscher und lassen sich von einem Bergführer begleiten. Max ist auch mitgekommen, er fotografiert, filmt und berichtet für eine Berliner Zeitung.
Trotz einiger Schwierigkeiten kommen sie am Hintereisferner an. Die Gruppe bewundert das Tal, das mal vom Gletscher ausgefüllt war. Letzte Woche hat es geschneit und der Gletscher hat etwas zugenommen, sagt der Bergführer. Im Sommer nimmt er wieder ab. Aber wie kann man die Eiszu- oder -abnahme messen?
In ihrem Matheunterricht hatten sie im Mathebuch eine Aufgabe gefunden, wo eine Formel für das Gletschervolumen in Abhängigkeit von der Zeit diskutiert werden sollte. Diese sagte für kurze Zeit Stabilität voraus und für lange Zeit eine Eiszeit.
Daten für Gletscherparameter
Der Bergführer erklärt ihnen, dass der Hintereisferner seit 1770 vermessen wird. Es gibt Daten zur Position der Zunge, der mittleren Eisdicke und der Volumenbilanz. Ein internationales Forscherteam hat sich zusammengetan, sammelt die Daten und versucht, Vorhersagen zu machen.
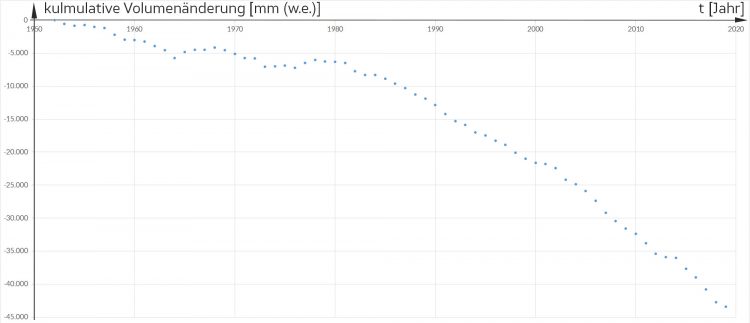
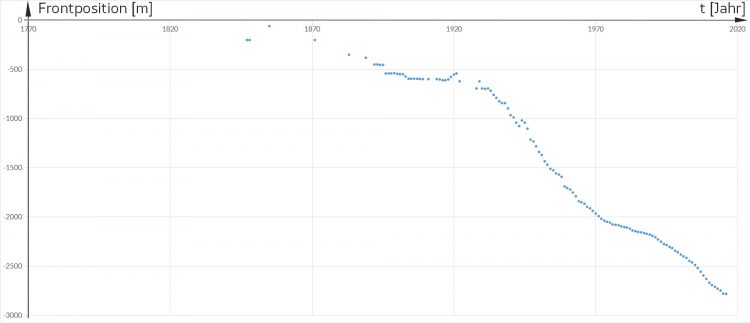
Polynomnäherung für Gletscherparameter
Charly Kinder, was meint ihr, wie könnten wir mit diesen Daten die Position der Zunge voraussagen?
Justin Na, wir können ja mal ‘ne Kurve durchlegen, sowie im Mathebuch. ‘ne Kurve 3. Grades könnte ich berechnen.
Charly Na, gut. Dann brauchen wir 4 Punkte, durch die wir die Kurve legen. Welche sollen wir denn nehmen?
Fabian Ich weiß es, ich weiß es, wir nehmen den ältesten Punkt und den aktuellsten, und dann noch welche dazwischen, vielleicht so:
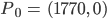
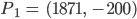
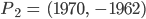
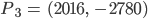
Charly Okay! Und wie finden wir die Koeffizienten für das Polynom 3. Grades?
Justin Wir setzen die Werte in einen Ansatz ein:
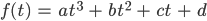
Charly Okay! Dann haben wir 4 Gleichungen für 4 Unbekannte. Kannst du das lösen?
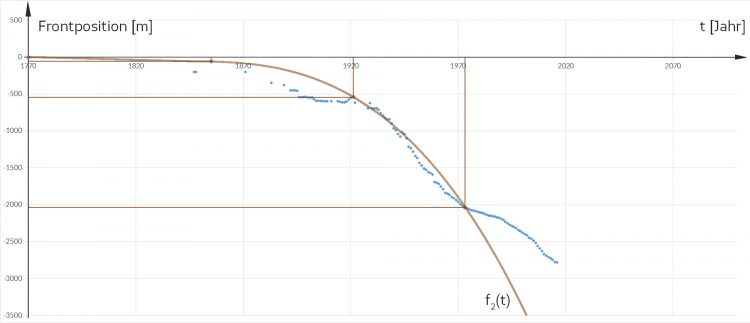
Justin Na, klar, ich weiß, wie das geht. Die Koeffizienten im linearen Gleichungssystem sind zwar etwas groß … aber okay, ich hab‘s. Hier ist mein Bild:
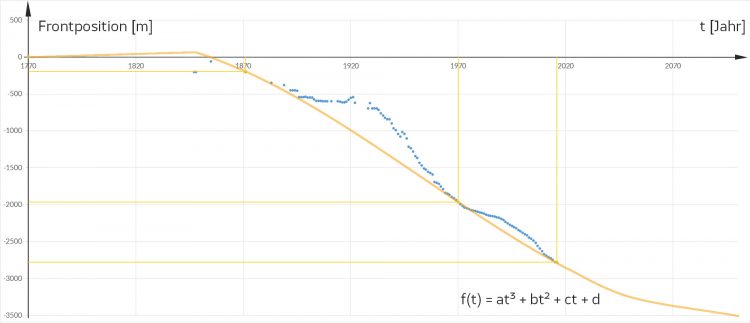
vom 3. Grad durch 4 ausgewählte Messpunkte mit a > 0.
Für 2100 haben wir dann einen Rückgang des Gletschers von 3500 m seit 1770. Auf jeden Fall nimmt der Gletscher erst mal ab.
Kritik
Finja Sag mal, Justin, deine Kurve geht ja nur durch 4 Punkte. In allen anderen Punkten ist sie sehr ungenau. Wie kannst du aufgrund von 4 Daten aus 100 Daten irgendetwas vorhersagen?
Fabian Naja, aber dass der Gletscher immer mehr zurückgeht, ist ja klar.
Finja Justin, wie groß ist denn dein Wert für a?
Justin Er ist 0.000321.
Finja Was, er ist positiv? Dann wird wieder ansteigen, genau wie bei der Berechnung der Eiszeit im Mathebuch!
Justin O shit!
Charly Das erinnert mich an den Wetterbericht – Vorhersagen sind wirklich schwierig! Ich meine auch, dass unser Polynom nicht geeignet ist.
Fabian Sollen wir den mittleren Wert des Rückganges berechnen und dann abschätzen?
Finja Das wäre ja noch schlimmer, das wäre eine lineare Näherung!
Charly Finja hat Recht, das bringt nichts. Außerdem haben wir nicht beachtet, dass auch diese Daten Mittelwerte sind. Jetzt ist der Gletscher wieder etwas länger, doch im Sommer schmilzt er. Das, was im Sommer geschmolzen ist, kann nur durch neuen Schnee ersetzt werden. Wenn die mittlere Tagestemperatur um -1°C liegt – da fängt nämlich das Eis schon zu schmelzen an wegen des Salzgehaltes – dann wird das Eis tagsüber schmelzen, das Gletscherwasser wird das Tal herunter fließen, und erst wenn es nachts kälter wird …
Finja … dann friert das Eis wieder fest, aber es ist weniger geworden. Das heißt, Charly, das Eisvolumen und die Zungenlänge hängen vom Temperaturverlauf jedes einzelnen Tages und vom Berg selbst ab?
Bergführer Stimmt! Sag mal, Justin, was hast du denn für 2020 berechnet?
Justin Moment, …, da liefert mein Polynom -2856 m.
Bergführer Das hatten wir schon letztes Jahr erreicht. 2019 und 2018 waren die Sommer sehr warm, der Gletscher ist viel schneller geschmolzen, die Daten sind in dieser Liste noch nicht drin, aber ich weiß es, ich kenne die Gegend hier, ich kenne die Berge und das Wetter.
Charly Stimmt. So einfach mit einer Interpolation lassen sich die Gletscherparameter nicht vollständig bestimmen. Aber in ein paar Tagen können wir das mit den Forschern selbst besprechen. Deshalb sind wir ja hier, wir wollen verstehen, welche Prozesse ablaufen. Ich will das auch verstehen, schließlich hängt viel davon ab.
Justin Charly, was können wir hier machen? Sind wir umsonst hier hoch gegangen?
Ausblick
Bergführer Nein, so eine Bergtour ist niemals umsonst. Schaut euch den Gletscher genau an, schaut Euch das Eis genau an! Wie ist es aufgebaut, welche Temperatur hat es jetzt an der Oberfläche und weiter unten, vielleicht könnt ihr eine kleine Probe nehmen und die Dichte messen?
Fabian Ja, das machen wir. Ich habe das Thermometer, Justin, schreibst du das Protokoll?
Justin Klar!
Finja Ich messe die Dichte.
Übungsaufgaben
- Bestimme das Polynom
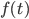! - Wie ändert sich die Kurve für andere Wertepaare?
Lösungen
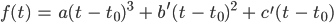
mit
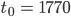
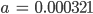
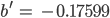
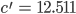
- Für die Punkte
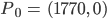
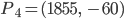
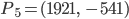
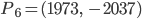
erhält man das Polynom
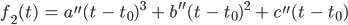
3. Grades mit negativem Koeffizienten
:
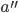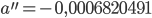
und
