Ben und Rike sind gut ins neue Jahr gekommen. Voller Tatendrang will Ben den Müll runterbringen und schaut sich die Mülltüten an.
Ben So eine Mülltüte hat die Innenmaße 47 cm (Länge) und 46,5 cm (Breite). Wenn sie so daliegt, hat sie eine Höhe von ca. 1 mm. Da komme ich auf ein Volumen von
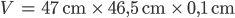
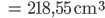
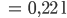
Hmm, irgendwas stimmt da nicht, das sollten doch 20 l sein!
Rike bringt nun den Müll runter und erschreckt sich, als sie Ben bei der Vermessung der Mülltonnen trifft.
Rike Mann!!! Du hast mich erschreckt! So kommst du nicht weiter!
Ben Das ist vielleicht ein Mist! Und wie soll‘s gehen? Sollen wir den Müll in die Spree werfen und die Verdrängung messen? – Ganz nach Archimedes!
Rike Du bist wohl von allen guten Geistern verlassen!
Ben Wieso? Hast du etwa eine Formel für den Inhalt?
Rike Lass uns zusammen überlegen, welche geometrische Form das ist:
Ben Na, eine Mülltütenform!
Rikes Parabelansatz
Rike Haha. Sieh doch mal, sie beult sich in der Mitte so aus, was hältst du davon, wenn wir für die eine Kante eine Parabel ansetzen?
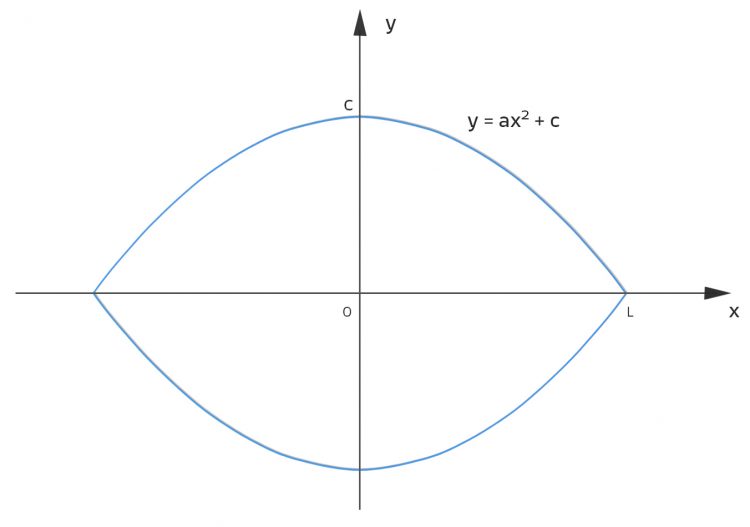
Ben Okay. Gar kein b?
Rike Das lineare Glied entfällt doch, meine Mülltüte soll symmetrisch sein.
Ben Na!
Rike Weil die Außenkante einen festen Umfang hat, …
Ben … nimmst du an!
Rike Ist ein Versuch, Ben, die Tüte soll nicht dehnbar sein, komm, gib nicht gleich auf!
Ben Und wenn dein Modell nicht lösbar ist?
Rike Du bist und bleibst ein sturer Informatiker!
Ben Danke!
1. Gleichung für a und L aus dem Umfang
Rike Bitte, gerne! So kriegen wir schon die erste Gleichung. Wir nehmen die Formel für die Weglänge: Bei uns ist die Weglänge bekannt, im 1. Quadranten haben wir
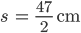
Andererseits
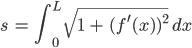
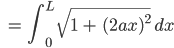
Jetzt nehme ich die Standardsubstitution
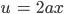
und damit wird
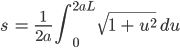
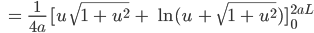
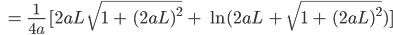
Ben Also – was ist deine 1. Gleichung?
Rike Na,
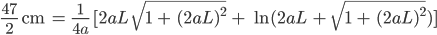
oder
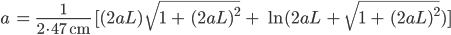
Ben Aha!
Rike Na, schau mal, jetzt haben wir einen Zusammenhang von a und 2aL, wir können es zwar nicht direkt auflösen, aber vielleicht kannst du mal berechnen, wie das aussieht?
Ben Okay! a als Funktion von 2aL.
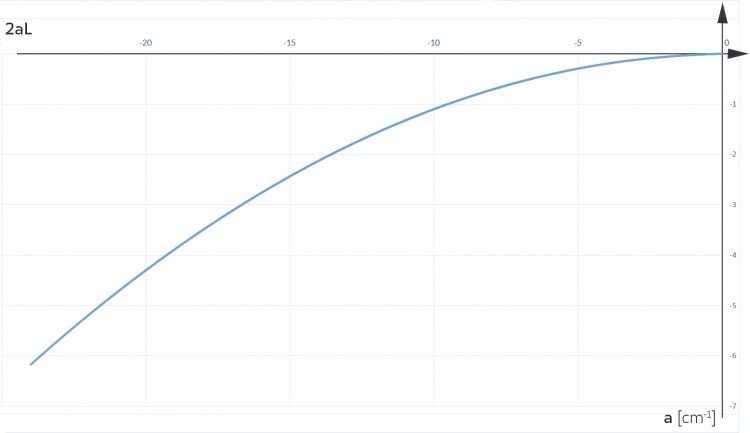
Jetzt können wir für jeden Punkt der Kurve
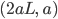
L berechnen, stimmt‘s?
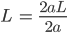
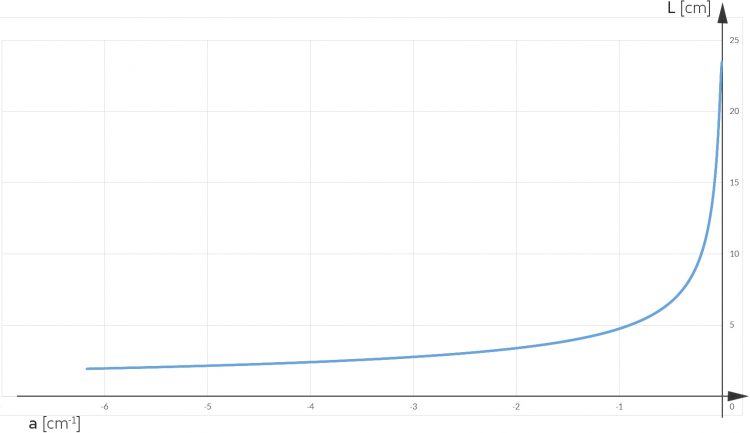
Rike Ja, stimmt. Jetzt kommt die Grundfläche dran.
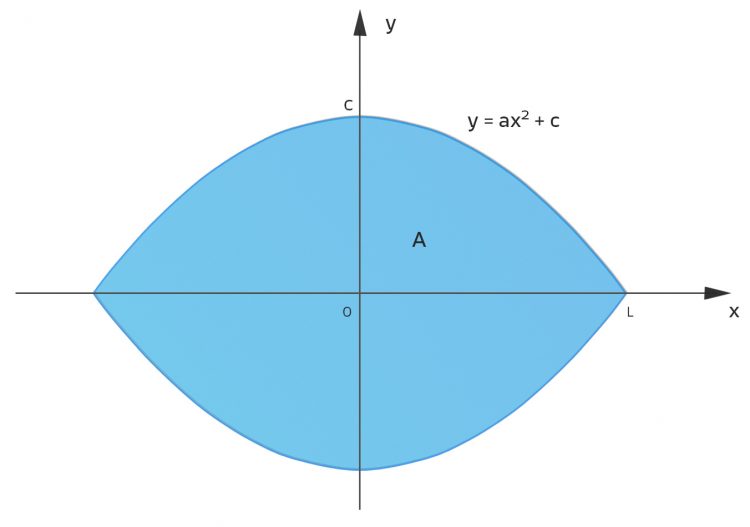
2. Gleichung: Grundfläche
Ben Okay, das können auch Informatiker!
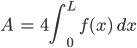
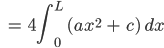
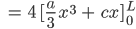
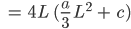
Wie finden wir das Absolutglied c?
3. Gleichung: Absolutglied c
Rike Wenn wir L haben, dann können wir c bestimmen, weil (L, 0) auf der Parabel
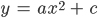
liegt, kriegen wir für
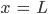
jetzt
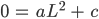
oder
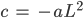
Ben Gut, dann kann ich dir die Fläche in Abhängigkeit von a berechnen – oder wenn du willst, können wir auch gleich das Volumen berechnen, wir brauchen ja nur mit der Höhe zu multiplizieren?
Volumenberechnung
Rike Ja, stimmt,
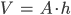
und
Ben Okay, hier schau mal: Das Volumen in Abhängigkeit von a für Parabel-Mülltüten:
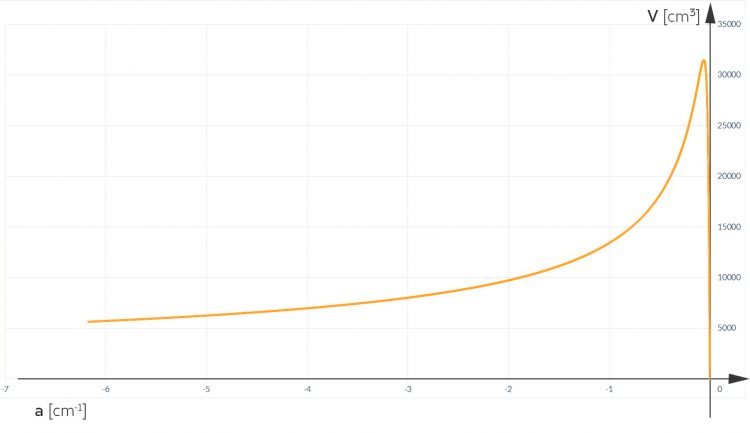
Rike Hey, Ben, mein Modell funktioniert! Das Volumen wird für ein a nahe Null maximal! Welches a ist das denn?
Ben Ach, warte, das ist
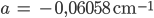
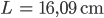
Das Volumen wird sogar

Rike Hey, schade, dass wir dann die Tüte oben offen lassen müssen!
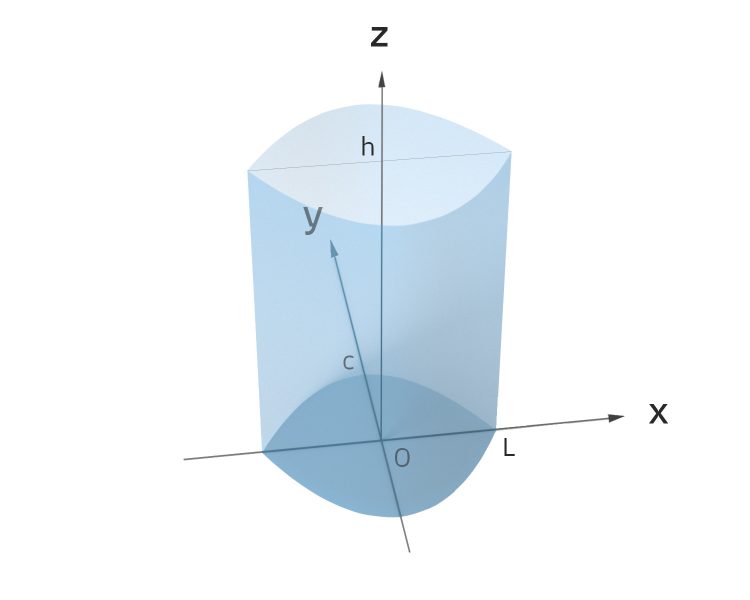
***
Übungsaufgaben
- Berechne c für das Volumenmaximum!
- Wie groß wird das Volumen, wenn die Tüte oben geschlossen wird? Ein Näherung wäre, sie oben umzuknicken, also eine neue Höhe h' = h - c zu wählen.
Lösungen
- 15,68 cm
- 20,4 l