Zwischen den Tagen sind Jenny und Lila in Berlin geblieben. Heute treffen sie sich, um das Pendel von Jennys Opa weiter zu studieren. Bisher haben sie nur die Näherung für kleine Winkel, die zu einer Schwingung mit der festen Periode
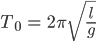
führt. Doch die Uhr bleibt manchmal stehen; und wenn die Anfangsauslenkung fast bis ganz nach oben geht, dann braucht das Pendel gefühlt sehr lange für eine Schwingung. Sie meinen, die Periode kann nicht unabhängig von der Auslenkung sein. Jenny und Lila haben das nichtlineare System numerisch mit dem Runge-Kutta-Verfahren gelöst, aber sie haben keine Gewissheit, dass die Lösung richtig ist. Nahe des Überschlags (θ0 = 180^°) sind sie sich sicher, dass es Ungenauigkeiten in ihrer Runge-Kutta-Lösung gibt. Tatsächlich können sie nur bis ca. 170° eine periodische Lösung interpretieren.
Das energetisch-analytische-elliptisches-Integral-Modell
Jenny Lila, ich habe noch einen anderen Ansatz gefunden. Man nimmt eine andere Herleitung: Mit Hilfe des Energieerhaltungssatzes kriegt man die DGL
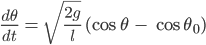
θ …. Winkel der Pendelauslenkung im Bogenmaß
θ0 … die Anfangsauslenkung
l … Länge des Pendels
g ... Erdbeschleunigung
Lila Na, super!
Jenny Aber wir brauchen das nicht zu lösen, wir wollen ja nur die Periode T in Abhängigkeit von θ0 bestimmen. Da findest Du eine exakte Herleitung bei Wiki und kriegst:
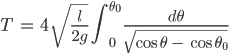
Lila Okay, ist ja immerhin eine Formel.
Jenny Ja, aber die hat's in sich. Man kann zeigen, dass für
das Integral divergiert und die Periode nach unendlich geht:
Lila Dein energetisch-analytisches Modell sagt, dass für eine 90°-Auslenkung die Periode unendlich groß wird?
Ellipitisches Integral
Jenny Ja! Und so geht es weiter? Um es zu berechnen, formt man es um: Mit der Substitution
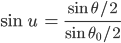
erhältst Du ein elliptisches Integral 1. Ordnung
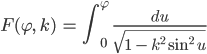
Lila Macht Ihr das bei Euch an der Uni?
Jenny Klar. Für solche elliptischen Integrale ist bekannt, dass sie für
divergieren.
Lila Oooh! Jennys energetisch-analytisches-elliptisches-Integral-Modell!
Jenny Haha! Bei uns führt dies alles zu der Formel
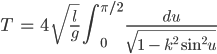
und
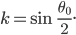
Numerische Berechnung des elliptischen Integrals
Lila Okay, jetzt muss ich nur das Integral numerisch nähern. Wir haben in unserem Analysiskurs gelernt, dass das Integral I über einer Funktion f als Grenzwert von
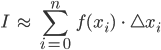
definiert wird.
Jenny Richtig, das Riemann-Integral. Was willst Du für Stützpunkte xi nehmen?
Lila Lass uns einfach die linken Ränder der Intervalle nehmen. Warte, das kann ich programmieren. Welchen Anfangswert sollen wir nehmen?
Spezialfall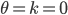 
Jenny Fang doch mal bei
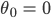
an!
Lila Nehmen wir wieder l = 1 m?
Jenny Ja.
Lila Sind 1000 Schritte okay?
Jenny Klar!
Lila Okay, dann wird unser k=0 und Lilas bester Integralnäherung erhält – trara!
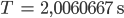
Jenny Super, das kann ich auch analytisch lösen, ich kriege für den Integranden 1 und für
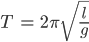
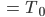
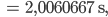
das war die Periode fürs linear genäherte Pendel?! Okay! Dann nimm doch mal die Werte, die wir für die Runge-Kutta-Näherung benutzt haben!
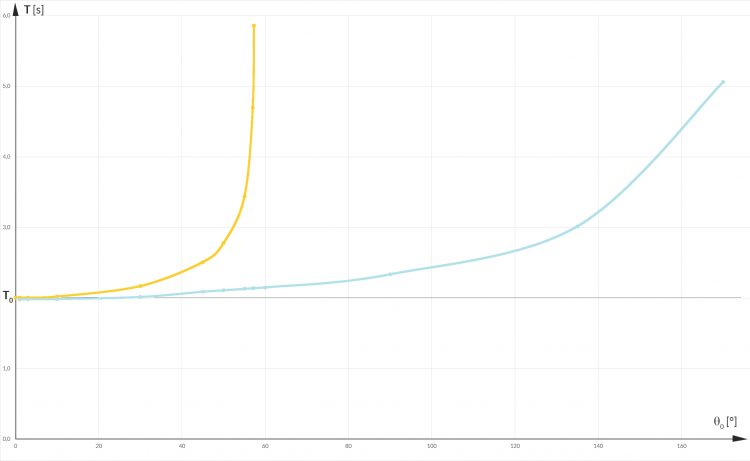
Vergleich der Perioden aus dem Runge-Kutta-Verfahren
Lila Warte, …, hier, ohh, bei
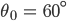
kriege ich keine endliche Zahl!
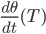hat einen Vorzeichenwechsel und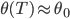 
Jenny Da ist schon Schluss? Jetzt weiß ich, warum ich Numerik hasse!
Lila Hahaha, schau mal, Dein elliptisches Integral hat doch auch Vorteile!
Jenny Ja, es ist echt super! Lass uns doch mal die Periodendauer an der Pendeluhr messen. Hast Du eine gute Stoppuhr dabei?
***
Übungsaufgabe
Welche Vorteile hat die energetisch-analytische Methode gegenüber dem Runge-Kutta-Verfahren?
Lösung
Das Verfahren zeigt periodische Lösungen des nichtlinearen Problems für 0 ≤ θ0 < 90°. Bei sehr kleinen Anfangswinkeln θ0 stimmt die Periode genau mit der des linearen mathematischen Pendels überein. Das Runge-Kutta-Verfahren berechnet ab θ0 ≥ 60° nur fastperiodische Lösungen, für θ0 = 0° wird keine periodische Lösung berechnet, also auch keine Periode T.