In dieser Woche besucht Lila wieder Jenny, weil sie die Gleichung für das mathematische Pendel noch nicht gelöst haben, nur eine Näherung für kleine Winkel.
Lila Hi, Jenny, wie geht’s? Schlägt das Pendel an der Uhr noch aus?
Jenny Haha, danke, komm rein. Ich habe über das Pendel nachgedacht und weiß nicht, ob wir beide das schaffen. Alle Physiker, also fast alle, nehmen immer die lineare Näherung. Aus sin θ wird θ, und dann ist das System exakt lösbar.
Lila Aber warum sollen wir uns mit kleinen Schwingungen zufriedengeben? I dare you, wie heißt das deutsch?
Jenny Ist schon gut. Ich erkläre Dir die Theorie und Du holst mal Dein Notebook raus. Dann sehen wir mal.
Lila Klar, das Notebook hab‘ ich dabei.
Mathematisches Pendel
Jenny Also, wir haben das Setting:
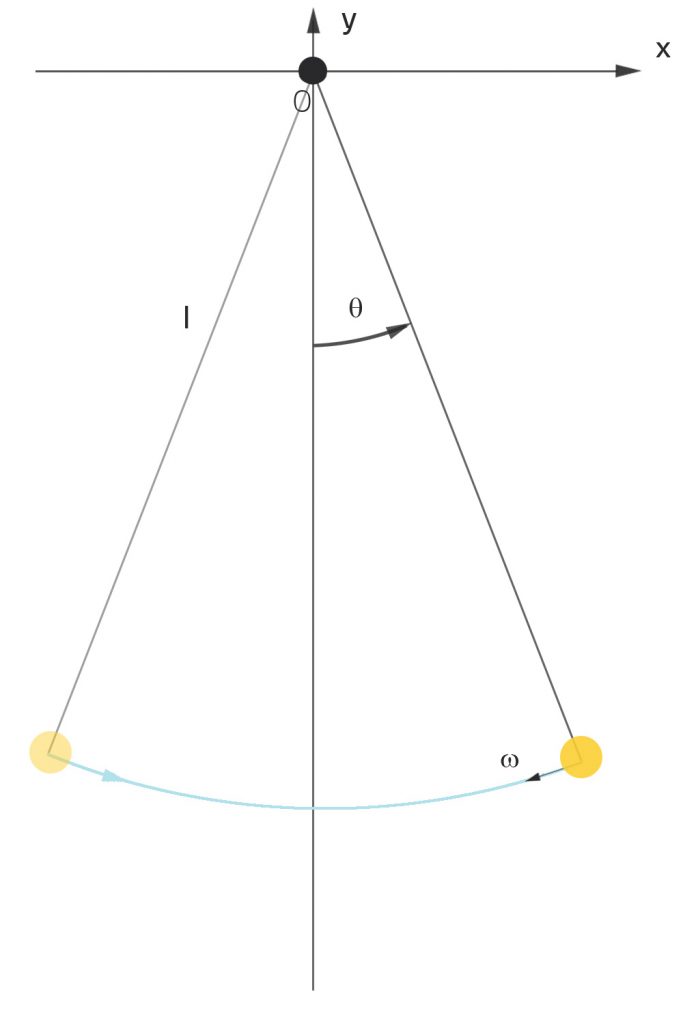
l … Länge des Pendels
m … Masse des Pendels
θ … Auslenkung im Bogenmaß
ω … Änderung des Winkels θ
g … Erdbeschleunigung
Dann kriegen wir die nichtlineare Differenzialgleichung 2. Ordnung:
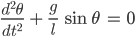
Die kann man schreiben als System von 2 Gleichungen:
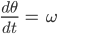
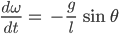
Dieses System hat offensichtlich 2 Gleichgewichtszustände:
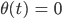
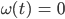
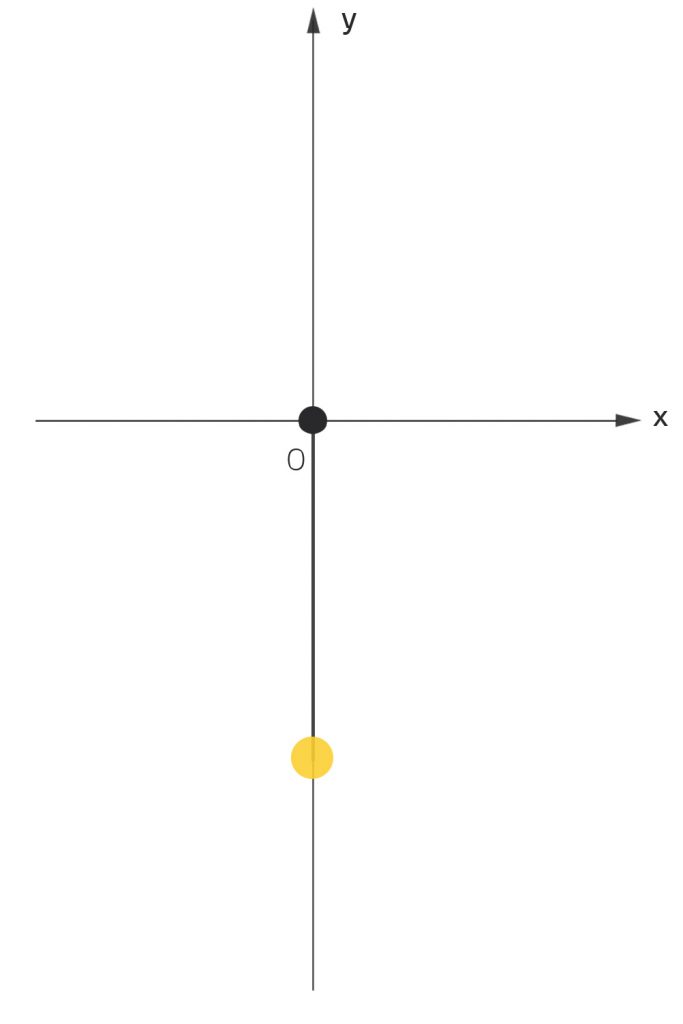
und
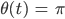
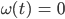
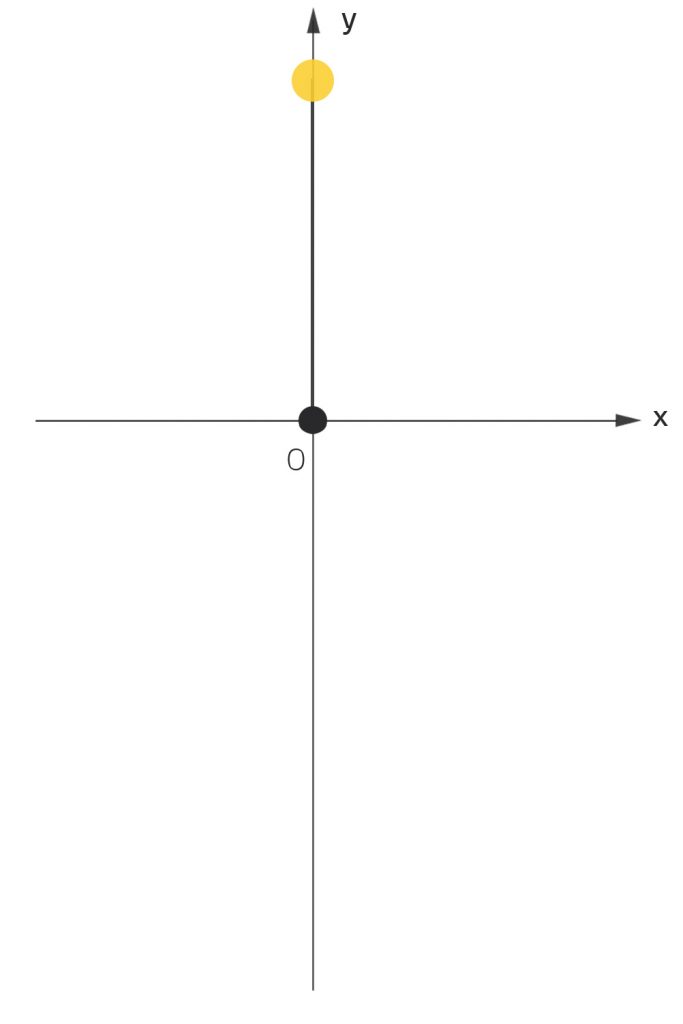
Lila Okay, verstehe. Aber wieso ist die Lösung
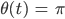
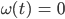
stationär?
Jenny Du kannst die Lösung in das DGL-System einsetzen – und es löst die Gleichungen. Die beiden Funktionen sind unabhängig von der Zeit, sie sind immer konstant, also stationär.
Lila Willst Du mir das mal mit Deiner Pendeluhr vorführen?
Jenny Nö, lass mal. Jedenfalls haben wir 2 stationäre Lösungen – auch wenn die eine instabil ist, sodass der normale Menschenverstand sagt, das ist keine Lösung.
Lila Na, gut! Erzähl mal, was hast Du an Deiner Uni gelernt?
Jenny Ich versuch’s. Unser Ziel ist es, periodische Lösungen zu finden und dann diese Perioden auf die Abhängigkeit des Anfangsausschlages untersuchen. Unser Modell hat keine Reibung, also müssten wir auch Lösungen finden, die periodisch sind, das heißt, die hin- und herschwingen – und das für ewig. Soweit das Modell.
Lila Ist ja gut. Mach mal los!
Jenny Ich kann Dir gar nicht garantieren, ob wir periodische Lösungen finden. Wir lösen nämlich ein Anfangswertproblem, jedenfalls versuchen wir’s. Das ist der Standardzugang.
Lila Hmm.
Jenny Welche Anfangswerte sollen wir denn nehmen?
Lila Wir nehmen die vom letzten Mal, so wie alle Physiker und Mathematiker!
Jenny Okay, das sind:
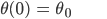
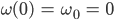
Lila θ0 ist die Anfangsauslenkung und ω0 = 0 steht für ein Pendel ohne Anfangsgeschwindigkeit, das Pendel startet aus der Ruhe ohne Schubs?
Runge-Kutta-Verfahren
Jenny Stimmt. Dann schlage ich das gute alte Runge-Kutta-Verfahren vor. Das geht so:
Zuerst diskretisieren wir die beiden Gleichungen wie folgt:
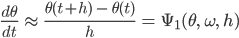
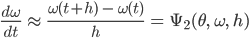
Die rechte Seite ist eine Linearkombination von der tatsächlichen rechten Seite mit verschiedenen Stützpunkten:
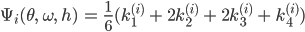
Und konkret ist das bei uns:
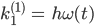
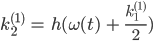
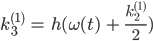
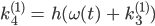
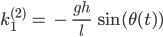
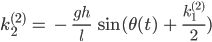
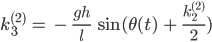
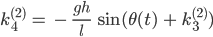
Lila Hey, Jenny, das kann ich doch alles berechnen!
Jenny Ja, mach mal! Du berechnest für jeden Zeitpunkt t die k’s – und zwar für jede der beiden Gleichungen und erhältst die Funktionen θ und ω zum nächsten Augenblick aus der Diskretisierung:
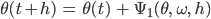
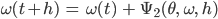
Weil das nur ein Schritt ist, heißt das Einschrittverfahren. Wenn wir auf die ganzen k’s verzichten und den einfachen Differenzenquotienten nehmen, wäre das zu gefährlich.
Lila Wieso?
Jenny Weil wir schon beim Anfangswert eine Näherung für den Anstieg benutzen, und dann wieder und dann wieder, das kann total aus dem Ruder laufen.
Lila Okay, die Linearkombination von verschiedenen Anstiegen ist dann besser?
Jenny Klar! Die konkrete Linearkombination kommt von Runge und Kutta.
Lila Schön. Wenn ich das jetzt mache, konvergiert die Lösung, die ich berechne, gegen die exakte Lösung?
Jenny Leider ist nicht klar, ob es Lösungen für alle Zeiten gibt, und wie die exakt aussehen. Aber wenn es solche geben sollte, dann konvergiert das Runge-Kutta-Verfahren für jeden Zeitpunkt t gegen die Lösung, für

Lila Okay. Dann lass mich anfangen. Wie groß soll ich h wählen?
Jenny Im linearen Modell hatten wir die Periode
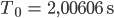
für kleine Auslenkungen. Lass uns mal dieses T0 durch 100 Schritte teilen.
Lila Okay, also
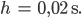
Dann kriege ich für
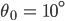
so eine, wie heißt das? – Runge-Kutta-Lösung?
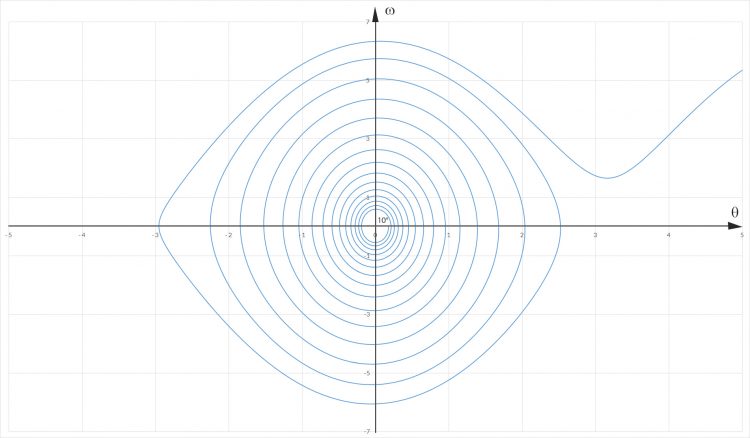
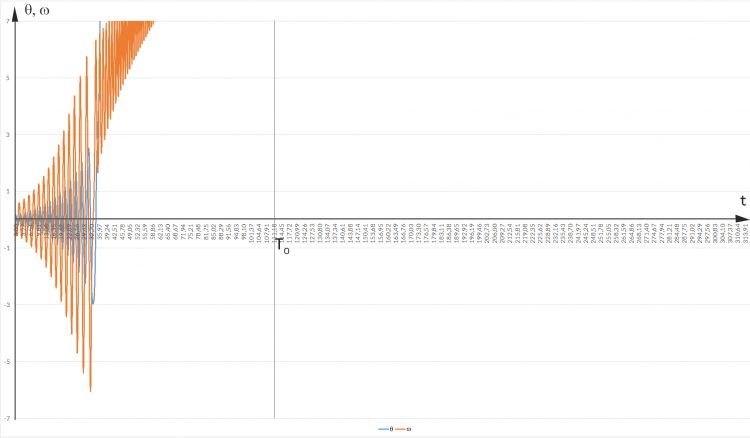
Jenny Oh, mein Gott!
Die Schrittweite h
Lila Das Pendel fängt bei 10° an und schwingt dann immer stärker, es überschlägt sich, zerstört das Gehäuse, die Uhr fällt um! Was haben wir falsch gemacht?
Jenny Zeig mal, hmm, das, das ist okay, hier, auch okay ….
Die Theorie sagt, für

konvergiert die Lösung.
Lila Okay, dann lasse ich mal

gehen! Schau, mal, Jenny, für
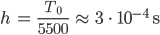
sieht das schon besser aus.
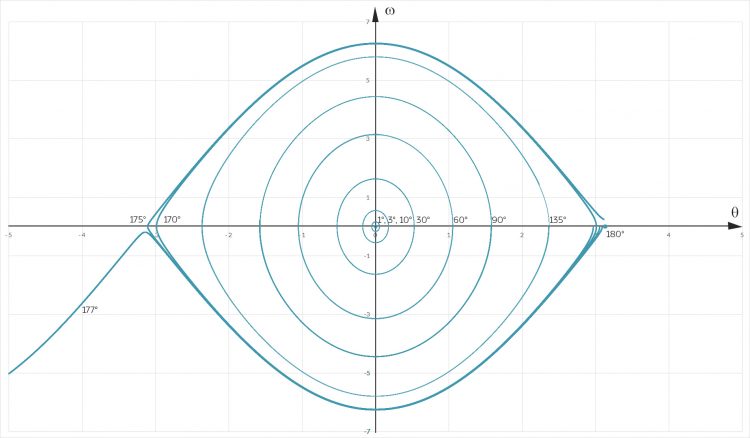
Zeitabhängigkeit der numerischen Lösungen (θ, ω) = (θ(t), ω(t))
Die Periode der regulären Schwingungen
Jenny Lila, Du bist ein Genie! Jetzt sehe ich auch, dass die Periode bei regulären Schwingungen mit der Auslenkung anwächst, solange es eben schwingt. Bei 177° Anfangsauslenkung überschlägt sich schon das Pendel?
Lila Das zeigt meine Runge-Kutta-Näherung mit h = 3∙10-4 s! Ich meine, da stimmt doch was mit der Energieerhaltung nicht?
Jenny Hahaha, na, da musst Du die Schrittweite h nach 0 gehen lassen!
Lila Hahaha! Das schafft mein Tabellenkalkulationsprogramm nicht. Das müssen wir zuerst verbessern.
Jenny Tolle Idee!
***
Übungsaufgaben
- Was passiert mit den Runge-Kutta-Lösungen für θ0 nahe 180°?
- Wie lässt sich das physikalisch interpretieren?
- Kann man auch θ0 > 180° wählen?
- Berechne weitere Lösungen für verschiedene Anfangswerte!
Lösungen
- Nahe 180° arbeitet das Verfahren nicht stabil.
- Der Gleichgewichtszustand ist (θ, ω) = (π, 0) nicht stabil.
- ja
