Lila studiert an einer Berliner Uni Mathematik und ist mittendrin im 1. Semester. Sie hat Jenny lange nicht getroffen und nichts von ihr gehört. Doch nun ist sie zu Jenny eingeladen. Jennys Opa ist gestorben und hat Jenny eine Pendeluhr hinterlassen. Die hat sie nun in ihrem Appartement stehen und beide Mädchen bewundern das gute Stück.
Lila Jenny, was hast Du solange gemacht? Hattest Du Probleme im Studium?
Jenny Ach, Lila, mein Opa ist gestorben. Ich bin nach Hause zu meiner Familie in die Provinz gefahren und bin dort bis zur Beerdigung geblieben.
Lila Jenny, es tut mir leid, dass Dein Opa gestorben ist.
Jenny Es ist traurig, ich war gerne bei ihm. Zu Hause habe ich etwas Abstand vom Studium gefunden und habe noch mal über die Linearität im Allgemeinen nachgedacht.
Lila Was die Welt im Innersten zusammenhält...
Jenny Ja, was die Welt im Innersten zusammenhält. Jetzt, wo ich die alte Uhr als Erinnerungsstück bei mir stehen habe, habe ich mich für das Uhrpendel interessiert. Da ist neben der Erinnerung an Opa auch die Erinnerung an die zugehörige Mathematik und Physik bei mir gekommen.
Lila Was gibt es da Interessantes?
Jenny Es gibt da eine Herleitung aus mechanischen Gesetzen, die geht so:
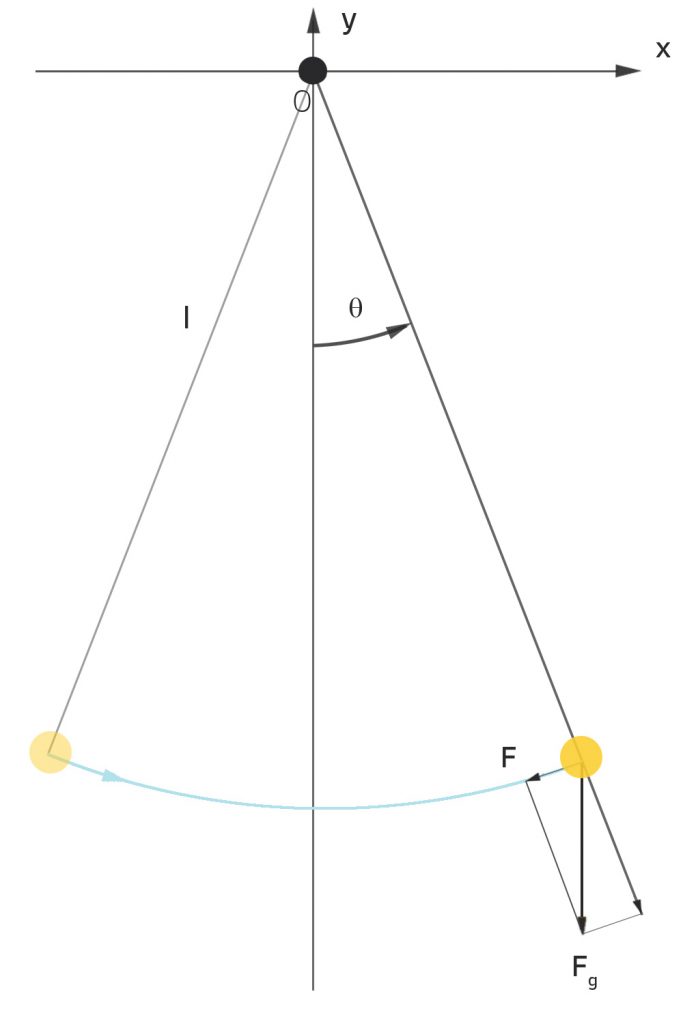
Mathematisches Pendel
Wir nehmen mal folgende Variablen:
l … Länge des Pendels
m … Masse des Pendels
θ … Auslenkung im Bogenmaß
s … der zurückgelegte Weg des Pendels
g … Erdbeschleunigung
Dann haben wir die Gravitationskraft Fg:
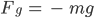
Der Teil von Fg, der das Pendel zum Schwingen bringt, ist:
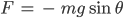
Andererseits ist der zurückgelegte Weg des Pendels:

Das leiten wir ab, um die Geschwindigkeit und die Beschleunigung zu berechnen:
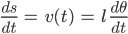
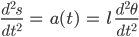
Tja, weiter, die Kraft F berechnet sich nach den Newtonschen Gesetzen aus
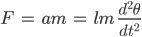
Wenn wir die beiden Kräfte am Pendel gleichsetzen – nach Newton! – haben wir:
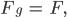
also
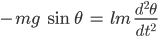
Hier kürzen wir zuerst die Masse und dann ist
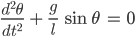
Lila Hey, kannst Du das einfach so herleiten? Hast Du das immer parat?
Jenny Nö, ich hab‘ mich damit beschäftigt und bin es mehrfach durchgegangen.
Lila Aha. Wie ist das mit der Reibung?
Jenny Das mathematische Pendel ist ohne Reibung, das heißt, es pendelt es ewig. Reale Uhren – wie Opas Pendeluhr – haben natürlich Reibung, aber die wird durch eine äußere Kraft, z.B. durch eine Feder kompensiert.
Lila Verstehe. Und jetzt?
Anfangswerte
Jenny Wir haben jetzt eine nichtlineare DGL für den Winkel θ. Dazu kommen noch die üblichen Anfangswerte
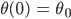
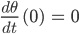
Lila Was bedeuten diese Anfangswerte?
Jenny Du lenkst das Pendel um den Winkel θ0 aus und lässt es ohne Krafteinwirkung los.
Lila Aha, verstehe. Und weiter?
Näherung
Jenny Diese nichtlineare DGL
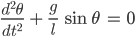
ist nicht explizit zu lösen, nur wenn man
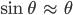
setzt – das ist für kleine Winkel okay, das haben die Physiker in ihrer Vorlesung gesagt und die Mathematiker ebenfalls in der Vorlesung für gewöhnliche DGL.
Lila Aha, Du zweifelst daran!
Jenny Naja, es ist die erste Näherung, und die wird in der einzigen Gleichung, die zu lösen ist, benutzt. Sie erfüllt natürlich ihren Zweck: Mit dieser Einschränkung kriegt man eine lineare DGL:
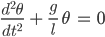
Und die hat genau eine Lösung. Das hatten wir im 3. Semester und haben das hoch und runter exerziert.
Lila Was habt Ihr gemacht?
Jenny Hahaha, sorry, wir haben das unendlich oft gerechnet!
Lila Unendlich oft?
Jenny Hahaha, ach das sagen wir so, jedenfalls sehr oft, bis wir die Lösung im Kopf ausrechnen konnten.
Lila Ehrlich?
Lösung des Anfangswertproblems
Jenny Na, hier ist die Lösung des Anfangswertproblems:
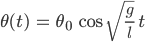
Du kannst es ja überprüfen!
Lila Okay, warte, …, ja, das stimmt.
Jenny Für verschiedene Anfangsauslenkungen θ0 erhalte kriege ich immer reine Kosinus-Schwingungen.
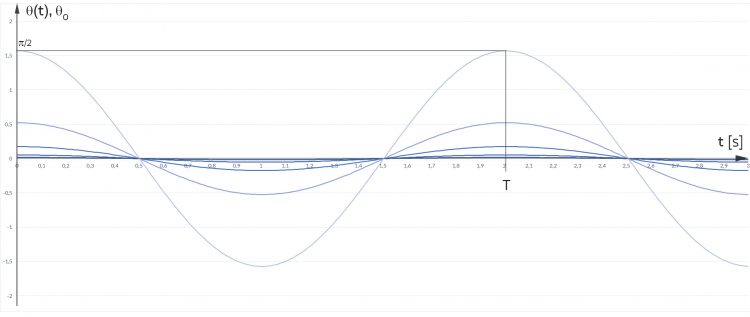
Die Periode ist immer gleich
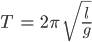
Sie hängt nicht von der Auslenkung ab. Sogar bei der Auslenkung
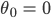
ergibt sich bei dem Modell dieselbe Periode T – obwohl gar nichts schwingt, die Lösung ist dann
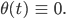
Als ich mir angeschaut habe, wie die Uhr stehengeblieben ist, bin ich auf den Gedanken gekommen, dass das lineare Modell hier nicht gilt.
Lila Wieso?
Jenny Bevor die Uhr stehen bleibt, wird das Pendel immer langsamer, der Ausschlag wird immer kleiner. Am Schluss schwingt das Pendel fast unmerklich und schließlich bleibt es stehen.
Lila Geht die Periode nach Unendlich?
Jenny Ja, sieht so aus! Das hat mich etwas aus der Fassung gebracht und ich habe versucht, die nichtlineare DGL zu lösen, bin aber nicht weit gekommen.
Lila Das interessiert mich, wollen wir nächste Woche weitermachen?
***
Übungsaufgaben
- Überprüfe Jennys Lösung des AWP.
- Löse die lineare DGL mit den AWen
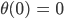
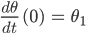
- Wie kann man diesen AW physikalisch interpretieren?
Lösungen
- Durch Einsetzen in die DGL.
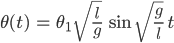
- Das Pendel wird nicht ausgelenkt, es hängt senkrecht nach unten und wird mit der Anfangsgeschwindigkeit θ1 "angestubst".