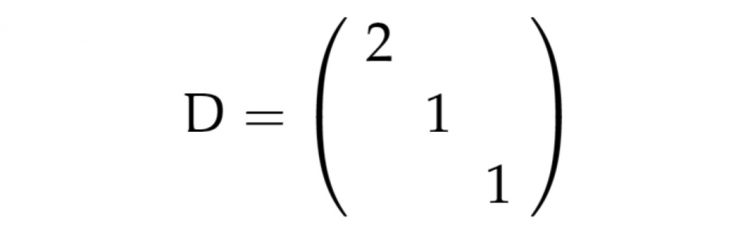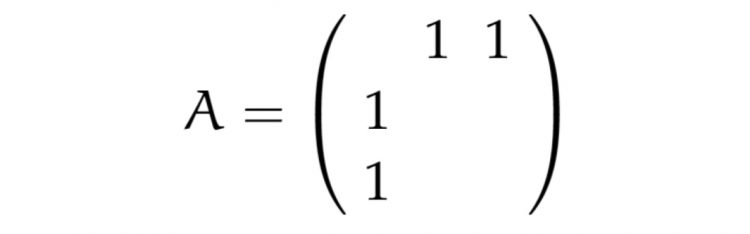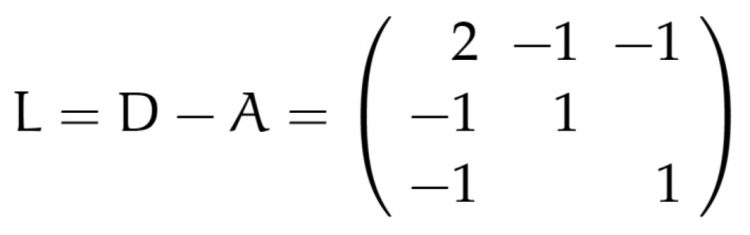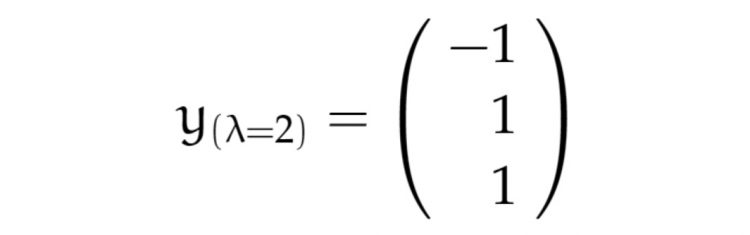Ben und Rike haben ein mittelgroßes Servernetz nach dem Einstein-Modell aufgebaut, getestet und simuliert. Als dann endlich alles lief, waren sie sehr glücklich. Sie haben ihre Präsi gehalten und sich ein paar Tage Auszeit gegönnt. Doch so einfach kann man nicht abschalten, wenn der Kopf voll mit Gedanken an Protokolle, Hard- und Software ist.
Ben mag Servernetze und liest alles, was es darüber gibt. Zwar kann sein Institut keine Rechnernetze aus 500 PCs aufbauen – nur so zum Test – aber mit wenigen PCs und vor allem mit Simulation könnte er noch viel größere Netze testen. Das geht natürlich auch am Strand. Jetzt hat er einen Artikel gefunden, wo man ein bisschen lineare Algebra, partielle DGln. und hyperbolische Geometrie zum Simulieren braucht. Da muss er doch Rike fragen.
Laplacian-based Network Embedding
Ben Hey, Rike, ich habe hier so ein Modell, wo ein Rechnernetz nach geometrischem und physikalischem Vorbild betrachtet wird – ein Laplacian-based Network Embedding.
Rike Aha! Wärmeleitungsgleichung?
Ben Stimmt!
Rike Klar, ist fast immer Wärmeleitungsgleichung, hab ich mir schon gedacht. Ein Server gibt seine Daten wie Wärme ab – stimmt‘s?
Ben Stimmt! Komm, lass uns doch mal das Modell durchgehen!
Rike Hey – ist das Deine Auszeit?
Ben Rike, glaubst Du, dass Informatiker wirklich Urlaub machen?
Rike lacht.
Ben Ich habe eine Arbeit von Gregorio Alanis-Lobato, Pablo Mier & Miguel A. Andrade-Navarro, verdammt noch mal! ….
Rike Sag das noch mal!
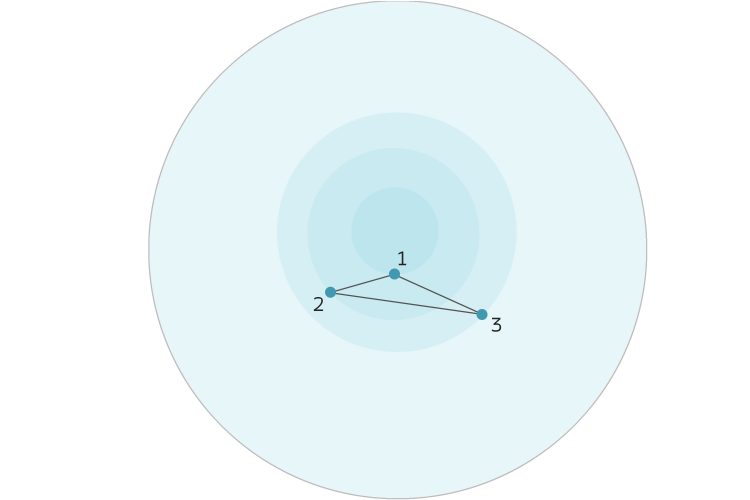
Ben Okay, lass es gut sein. Also die Drei starten mit einem Servernetz, das sich durch ungerichtete, ungewichtete Graphen beschreiben lässt. Das kleinste nichttriviale Netzwerk wäre so eins:
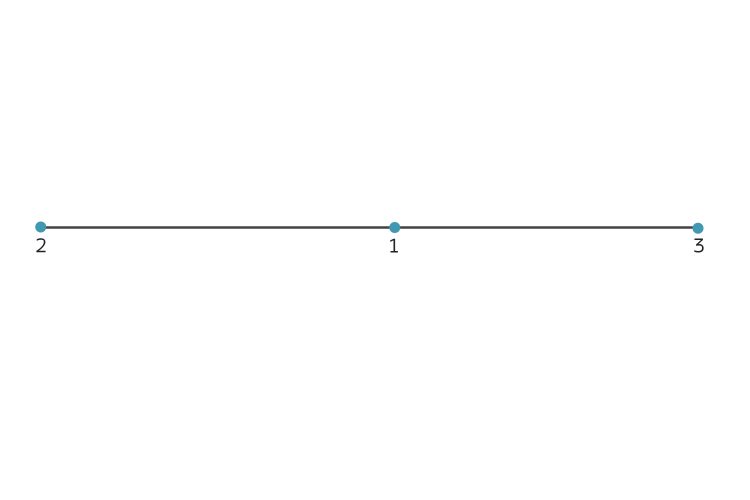
Den 1. Server – den mit den meisten Verbindungen – kann man als Wärmequelle interpretieren, wie Du Dir ja denken kannst.
Rike Ja – eine schöne Metapher. Für mich ist interessant, dass einige physikalische und mathematische Modelle, wie die Wärmeleitung, auch in der Informatik und in der künstlichen Intelligenz auftauchen und nützlich sind, als wären sie universell. Aber mal schauen, was es bringt.
Herleitung Laplacian
Ben Schön. Aus diesem Graphen wird nun ein Laplacian hergeleitet, für diesen werden die Eigenwerte und -vektoren berechnet und die hyperbolische Einbettung aufgestellt.
Rike Okay, zeig mal …. Aha. Zuerst nummerierst Du alle Vertices nach ihrem Degree durch, klar, das hast Du ja schon gemacht:
i = 1 … der Server mit 2 Verbindungen
i = 2 … der Server mit einer Verbindung
i = 3 … der 2. Server mit einer Verbindung
Für den Graphen sollst Du 2 Matrizen formulieren, eine in Diagonalgestalt D, da stehen die Degrees des i-ten Vertex in der i-ten Zeile, und eine Matrix A, da soll an der Stelle ij eine 1 stehen, wenn der i-te mit dem j-ten Server verbunden sind, sonst sind überall Nullen.
Ben Okay, bei meinem 3er Beispiel ist das dann
und
Rike Gut. Jetzt geht es weiter. Du bildest den Laplacian:
Ben Ach, iss ja nur ne Matrix!
Rike Naja, immerhin beschreibt sie vollständig das Netzwerk und hat eine Analogie zum Laplace-Beltrami-Operator in der Differentialgeometrie.
Ben Na gut.
Rike Immerhin ist er positiv definit und hat nur nichtnegative reelle Eigenwerte. Die bilden sein Spektrum.
Ben Schön!
Verallgemeinerte Eigenwerte und -vektoren
Rike Jetzt sollst Du sogenannte verallgemeinerte Eigenwerte λ und Eigenvektoren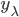 
finden:
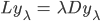
Ben Na schön, dieses D auf der rechten Seite wird schon seinen Grund haben, wenn das Netzwerk seine Daten abgibt, ist es sinnvoll, λ-Fache der Diagonalmatrix angewendet auf 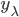zu suchen.
Rike Bloß gut, dass Du ein kleines Netz hast, hier kann ich Dir die λ's ausrechnen, für größere Netzwerke brauchst Du ein intelligentes Programm. Du musst
lösen, das gibt ein Polynom in λ vom Grad 3 und bei N Servern eben vom Grad N.
Ben Hmm. Und dann?
Rike Dann löst Du für jedes λ die Vektorgleichung
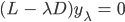
Aber warte mal, hier, Alanis-Lobato scheibt, dass Du hier nur 2 Eigenwerte und die dazugehörigen Eigenvektoren brauchst, die kleinsten positiven.
Ich rechne das mal aus, warte,…, okay, hier haben wir die Eigenwerte
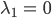
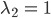
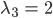
Die Eigenvektoren zu den positiven Eigenwerten sind:
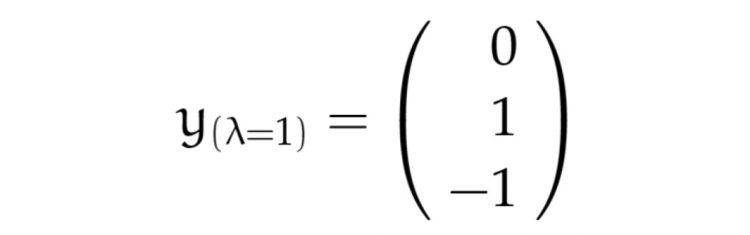
und
Ben Rike, toll, wie Du das machst, ich hasse lineare Algebra!
Rike Ja, ich weiß, wie alle Informatiker, wer will schon Determinanten ausrechen und lineare Gleichungen lösen!
Ben Genau! Und wie geht’s weiter?
Winkel der Einbettung
Rike Die beiden verallgemeinerten Eigenvektoren 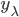zeigen in spezielle Richtungen und beschreiben, in welche Richtung der Laplacian wirkt. Ja, die Verhältnisse der Koordinaten ergeben die Einbettungswinkel θ1i in der hyperbolischen Ebene:
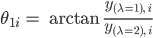
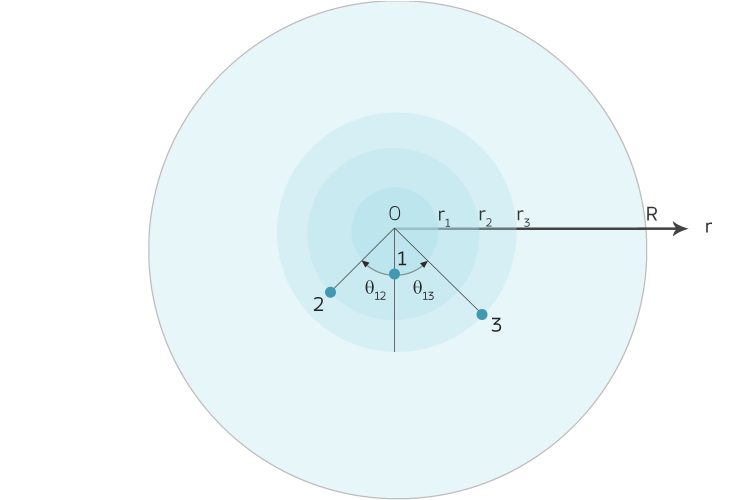
Bei uns ist das
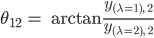
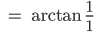
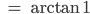
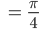
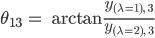
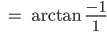
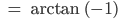
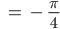
Ben Super!
Rike Jetzt fehlen noch die Radien.
Ben Klar, das kriege ich hin, da gibt es explizite Formeln. Anders als beim Einstein-Modell werden hier die Server mit gleichen Degrees nicht auf einem Radius angeordnet, hier werden die Radien immer größer, sie hängen von ein paar Konstanten ab:
Parameter des Netzes
γ ist ein Parameter des Netzwerkes, γ > 2, wie beim Einstein-Modell, er ist eigentlich ein Faktor zur Beschreibung der Verteilung der Grade, aus ihm wird der nächste Parameter β berechnet:
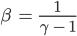
Dann haben wir noch:
… Anzahl der Vertices
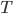…“Temperatur“ des Netzes,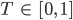 
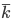… ist der mittlere Degree der Vertices
Radien der Einbettung
Den Radius des hyperbolischen Kreises können wir jetzt berechnen, die Formel lautet:
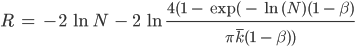
Weiter, der Radius ri jedes Vertex wird so berechnet:
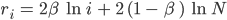
Rike Warte, ich berechne Dir das. Was sollen wir für γ und T nehmen?
Ben Wie beim letzten Mal:
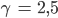
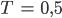
Rike Okay, dann hast Du:
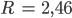
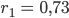
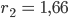
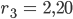
Ben Schön, das Netzwerk mit der Laplace-Einbettung selbst entsteht durch Verbindung aller Server i zu j, i > j:
Hyperbolische Abstände und Verbindungswahrscheinlichkeiten
Die hyperbolischen Abstände xij zwischen den Servern i und j sind wieder:
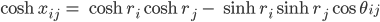
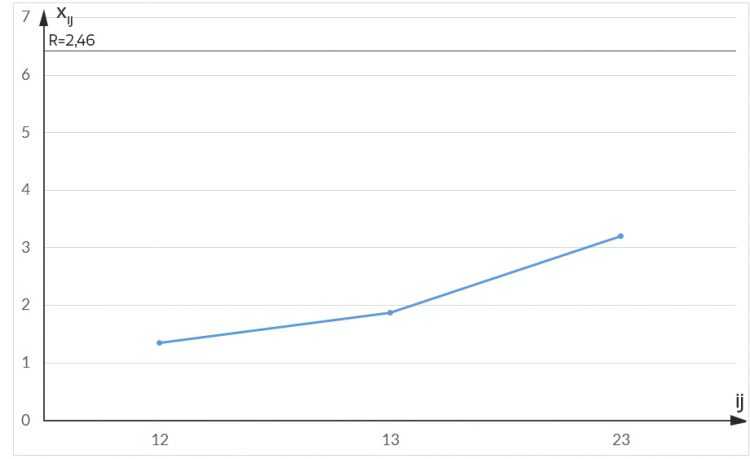
Daraus berechnen wir die Verbindungswahrscheinlichkeiten pij der Serververbindung ij mit derselben Exponentialverteilung und kriegen:
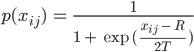
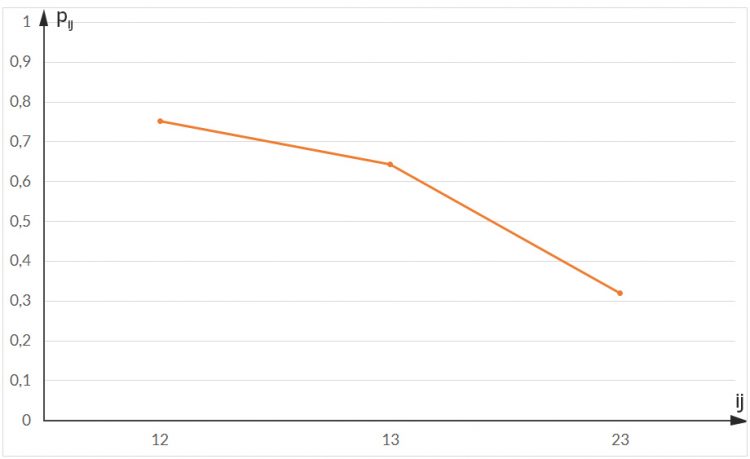
Ben Nicht schlecht! Die Verbindungswahrscheinlichkeit für die ersten beiden Server ist 0,75, für den 1. und 3. ist sie etwas kleiner: 0,64 und für den 2. und 3. Server ist sie 0,32. Das macht Sinn, das gefällt mir! Rike, jetzt verstehe ich es ganz gut, aber wer hilft mir, diese Eigenwerte und Eigenvektoren für größere Netze auszurechnen?
Rike Ich glaube, das hat schon jemand implementiert, Du brauchst es nur runterzuladen!
Ben Ooooh, dann tue ich das mal und wir können unsere kleine Auszeit fortsetzen!
Rike Hahaha!
***
Übungsaufgaben
- Wie drückt sich die Metapher der Wärmeleitungsgleichung mathematisch aus?
- Bleibt die Topologie des Netzes beim Laplacian-based Network Embedding unverändert?
Lösungen
- Man könnte die Anzahl der Verbindungen jedes Servers als Anfangstemperatur bzw. -datenmenge betrachten. Die Temperatur- bzw. Datenmengendifferenzen gleichen sich aus, die Lösungen sind nichtnegativ, man könnte ein Gesetz der Energieerhaltung und der Steigerung der Entropie formulieren.
- Nein, bei der Einbettung werden alle Knoten verbunden.