Ben hat in Nature Communications einen interessanten Artikel von Marián Boguñá und Kollegen über die Modellierung des Internets mit hyperbolischen Geometrien gelesen. Er versucht, das rechnerisch nachzuvollziehen, doch es ist schwieriger als erwartet. So fragt er Rike.
Ben Hi, Rike, ich hab‘ da so ein sogenanntes Einstein-Modell für das globale Internetsystem. Es geht darum, immer mehr Server zu verbinden, die Geometrie der Erde aufzugreifen und kurze Verbindungswege zu schaffen. Mit einer hyperbolischen Geometrie auf dem Kreis kann das sehr gut simuliert werden. Da passen (weiter draußen und am Rand) unendlich viele Punkte rein. Also genug Platz für zukünftige Server. Nur diese hyperbolische Geometrie, die macht mir echt zu schaffen.
Rike Na! Erklär doch mal das Einstein-Modell.
Ben Das geht so. Wir platzieren die Server der Welt auf einem Kreis. Eine Kugel wäre noch viel besser, aber wir fangen mit dem Kreis an. Wir könnten die Hälfte der Erde auf einen Halbkreis projizieren und die gegenüberliegende Seite au dem anderen Halbkreis. Okay?
Rike Klar! Aber das ist nicht das Problem?
Ein Netzwerk als Graph
Ben Nein. Zuerst haben wir so eine Art Graph. Die Vertices (Knoten) sind die Server, die Edges (Kanten) sind die Verbindungen. So, hier mal ein Beispiel.
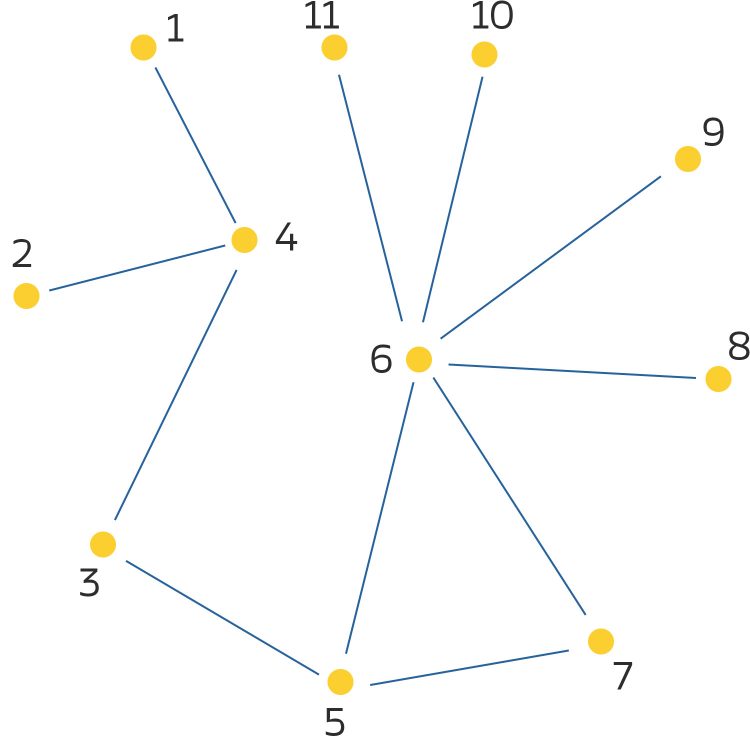
Rike Ich weiß.
Ben Jedem Vertex wird ein Degree k (Grad) zugeordnet. Das ist die Anzahl seiner Nachbarn, mit denen er verbunden ist.
Rike Na gut, in Deinem Beispiel ist
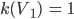
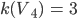
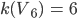
Ben Hast Du Dich schon mal mit Graphentheorie beschäftigt?
Rike Ach! Nö!
Das Einstein-Modell
Ben Okay. Jetzt wird im Einstein-Modell vorgeschrieben, dass die Vertices auf dem Kreis mit dem Mittelpunkt in Null gleichmäßig verteilt sind. Ungefähr so:
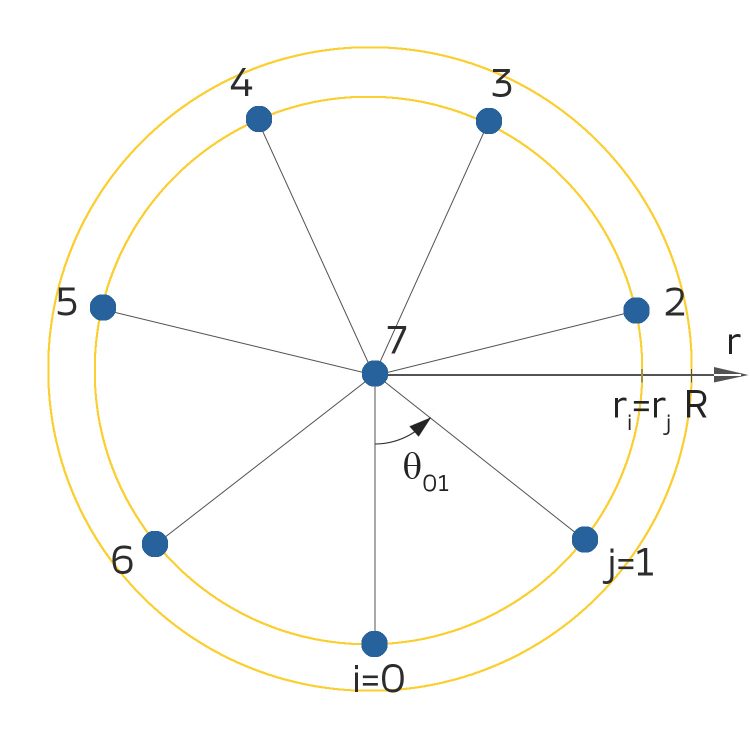
Und die radiale Verteilung der Vertices wächst exponentiell zum Rand R hin. Dafür gibt es eine Formel:
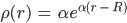
Rike Gut. Das zeichne ich mal. Was ist α?
Ben α ist ein Parameter. Warte, ich liste alle Parameter auf:
Freie Parameter
N … Anzahl der Vertices des Netzwerkes
γ … Exponent der Verteilung der Degrees: p(k) ~ k-γ, γ > 2
r … Radius eines Vertex, Abstand vom Mittelpunkt des Kreises
θij … Winkel zwischen den Verbindungen der Vertices Vi und Vj zum Nullpunkt
T … „Temperatur“ des Netzwerkes,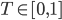 
Abhängige Parameter
α … Parameter, aus γ zu berechnen:
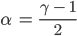
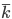… mittlerer Degree
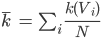
c … Maß für Clusterbildung
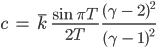
R … Radius des Modells
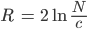
Rike Ooooh! Das hast Du Dir ja was Tolles ausgesucht! Also für T = 0,5, γ = 2,5 kriege ich
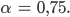
R hängt von N und der Topologie ab.
Ben Richtig. Lass uns unser kleines Beispiel mit N = 8 nehmen.
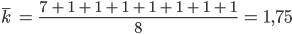
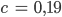
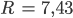
Radiale Verteilung der Vertices
Die Dichte ρ wächst dann exponentiell mit dem Radius r. Das ist klar.
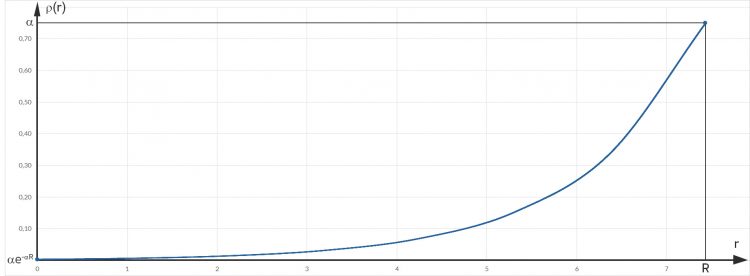
Hyperbolischer Abstand zweier Vertices
Jetzt fangen meine echten Schwierigkeiten an. Zwei Vertices Vi und Vj mit den Radien ri bzw. rj und dem Winkel θij zwischen ihnen bekommen den hyperbolischen Abstand xij, der soll so ausgerechnet werden:
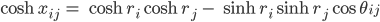
Diese Formel überschaue ich nicht. Ich habe echt kein Gefühl dafür. Außerdem macht mir dieser Areakosinus ein paar Probleme.
Rike Hey, Ben, paß auf. Ich zeichne Dir mal den Sinus hyperbolicus und den Kosinus hyperbolicus. Die kriegen für Dein R = 7,43 schon sehr große Werte nahe 800 und unterscheiden sich kaum noch.
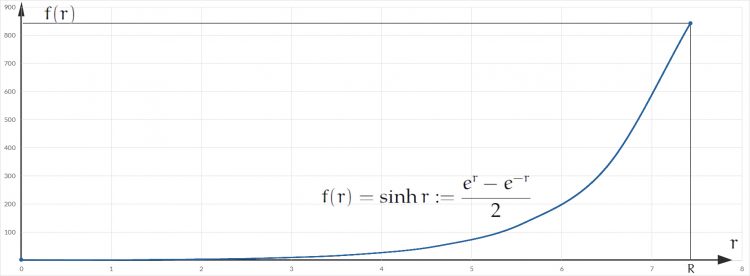
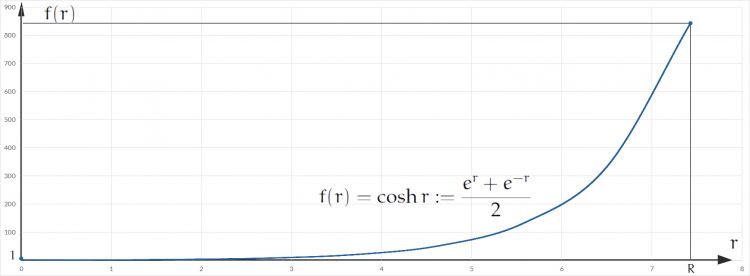
Bei Null (r = 0) kannst Du sie unterscheiden, wenn Du genau hinsiehst, denn es ist
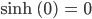
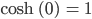
Und wenn Du die Umkehrfunktion von Kosinus hyperbolicus bildest, für
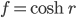
ist das
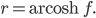
Diese Areakosinus hyperbolicus-Funktion ist nur für Werte f ≥ 1 erklärt. Verstehst Du, wenn die Werte für cosh xij kleiner als 1 werden, kannst Du keinen Areakosinus hyperbolicus bilden. Dann hast Du eine paar Ungenauigkeiten in Deiner Rechnung.
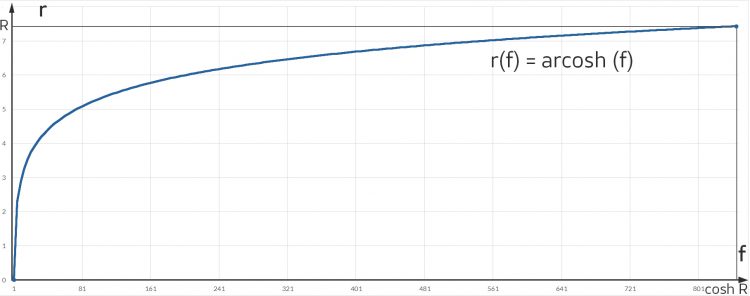
Ben Aaah, numerische Instabilität beim Punkt (1, 0), das muss ich prüfen. Doch ich habe immer noch keine Vorstellung von diesem hyperbolischen Abstand.
Spezialfall: 2 Vertices auf dem Durchmesser
Rike Weißt Du was, wir rechnen mal den Fall, wenn 2 Server auf dem Durchmesser des Kreises liegen.
Ben Ja, schön!
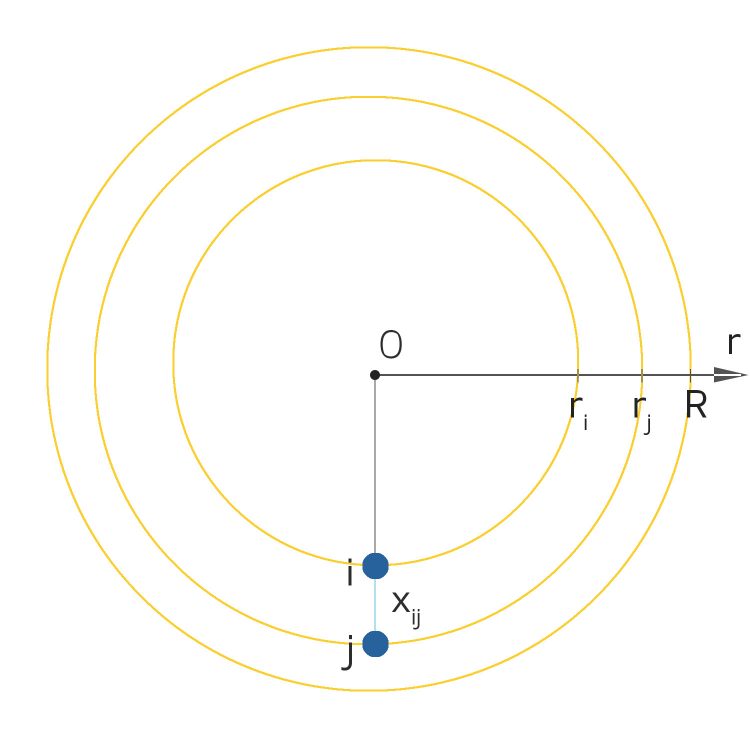
Rike Dann ist dieser Winkel θij zwischen ihnen
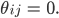
Ben Ja, dann wird
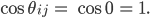
Rike Stimmt. Weiter!
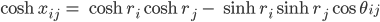
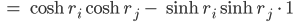
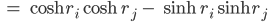
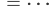
Jetzt nehmen wir ein Additionstheorem für die Hyperbelfunktionen:
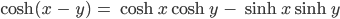
Ben Mensch, Rike! Ich Idiot nutze immer nur die Formel, ich implementiere die direkt, aber Du hast noch mehr Informationen, dann kannst Du die Fomel vereinfachen!
Rike Haha, quick and dirty! Die Informatiker! Lass mich das zu Ende bringen. Wir greifen die Formel für xij wieder auf:
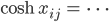
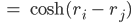
Jetzt wendest Du auf beide Seiten die Umkehrfunktion nur für nichtnegative Werte an und kriegst
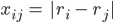
Richtig? xij soll nichtnegativ sein?
Ben Ja! Na! Jetzt habe ich den Abstand der beiden Punkte, der ist der Abstand der Radien, schön, aber der sieht mir doch recht euklidisch aus! Wo ist denn jetzt das hyperbolische?
Rike Auf dem Durchmesser ist er euklidisch. Der maximale Abstand auf dem unteren Halbkreis ist R und der minimale ist 0.
Hyperbolischer Abstand in Abhängigkeit vom Winkel
Ben Und wie ändert sich der Abstand zweier Vertices auf einem Kreis, wenn ich den Winkel vergrößere?
Rike Ach, wenn Du Deinen Computer einmal im Kreis herumschiebst?
Ben Rike, nein, einmal durch Europa!
Rike Haha, also wir setzen dann die beiden Radien gleich und lassen den i. Server stehen und der andere mit der Nummer j fährt im Kreis herum?
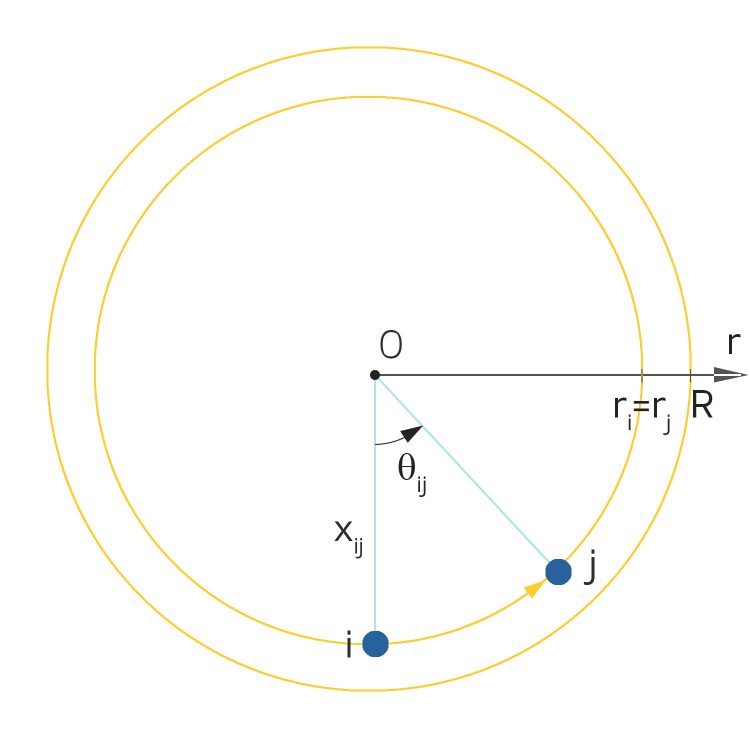
Ben Ja!
Rike Okay, analytisch vereinfacht sich nicht viel. Für
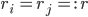
kriegen wir
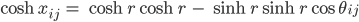
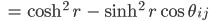
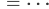
Weißt Du, da nehmen wir wieder ein Additionstheorem für die Hyperbelfunktionen:
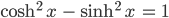
Das stellen wir nach dem Kosinus hyperbolicus um und kriegen:
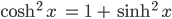
und das setzen wir in Deine Abstandsformel ein:
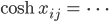
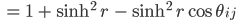
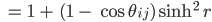
und schließlich
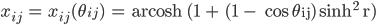
Tolle Sache!
Ben Was???
Rike Das können wir numerisch berechnen, hier, ist doch kein Problem!
Ben Was hast Du für einen Radius für die Kreisfahrt genommen?
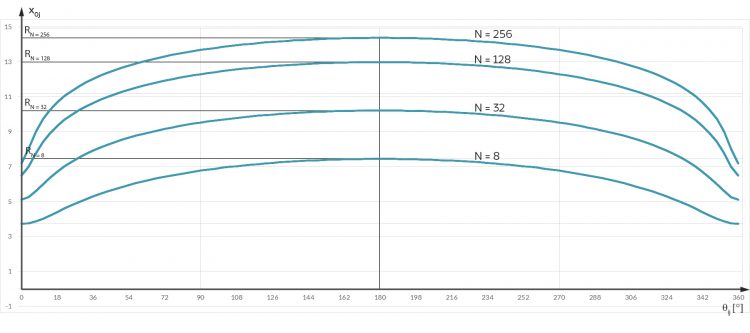
Rike Warte, für verschiedene Radien r kriege ich verschiedene Kurven.
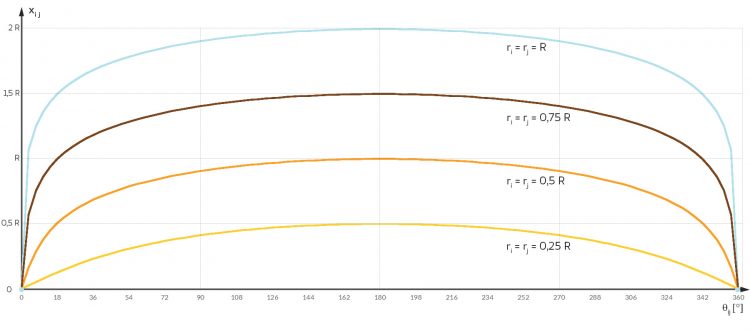
Ben Okay, weiter draußen sind die Abstände viel größer, schon bei der kleinsten Drehung! Ja gefällt mir, dieser hyperbolische Abstand. Super!
***
Übungsaufgaben
- Wie verändert sich R in Abhängigkeit von N und c?
- Wie wirkt sich das auf den Abstand xij aus?
Lösungen
- R wächst logarithmisch mit der Anzahl der Rechner N und fällt logarithmisch mit c.
- Für größere N wird R größer und damit gibt es auch größere Radien ri.
