Charly sitzt an diesem verregneten und windigen Osterferientag an einer „sportlichen“ Abiaufgabe. Es ist eine typische Analysis-Aufgabe über eine Funktionenschar mit einem Parameter. In dieser Aufgabe werden Nullstellenberechnung, Flächenberechnung, Kurvendiskussion, topologische Eigenschaften, numerische Näherungsverfahren, Zahlentheorie und nicht zuletzt eine Anwendung kombiniert. Die Aufgabe, die einen wissenschaftlichen Taschenrechner als Hilfsmittel zulässt, hat 13 Teilaufgaben. Man kann insgesamt für die Aufgabe 50 Punkte erhalten. Da kommt Rike dazu.
Schlagwort: Topologie
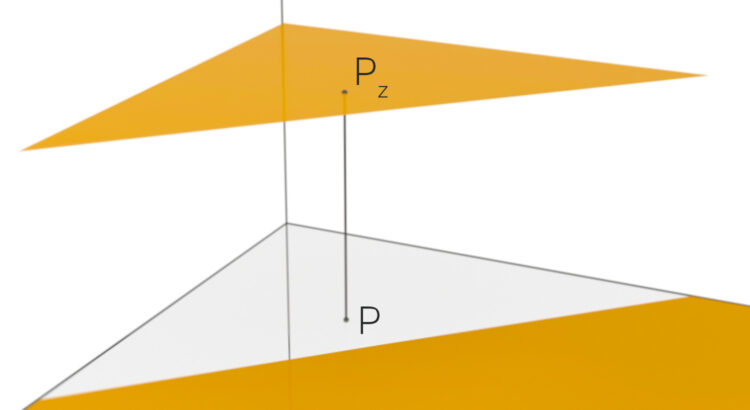
KI-Variationen einer Klausuraufgabe
Rike kommt für einen kurzen Besuch an ihre ehemalige Uni, wo sie früher Mathetutorien gegeben hat. Sie lässt sich die neusten Matheklausuren zeigen. Die von der 3D-Darstellung von Funktionen zweier Veränderlicher hat es ihr besonders angetan. Wie schön die ist, seufzt sie.

Hyperbolische Geometrie für Serververbindungen II
Ben und Rike hatten den hyperbolischen Abstand im Einstein-Modell für Computernetze diskutiert. Jetzt will Ben mit Rike die Netze selbst diskutieren. Das Modell ist nicht so einfach zu verstehen und vor lauter Modellbetrachtungen kommt Ben nicht auf den Punkt. Sein Ziel ist es, selbst so ein Netz aufzubauen und vorher zu simulieren Weiterlesen

Hyperbolische Geometrie für Serververbindungen I
Ben hat in Nature Communications einen interessanten Artikel von Marián Boguñá und Kollegen über die Modellierung des Internets mit hyperbolischen Geometrien gelesen. Er versucht, das rechnerisch nachzuvollziehen, doch es ist schwieriger als erwartet. So fragt er Rike.
Ben Hi, Rike, ich hab‘ da so ein sogenanntes Einstein-Modell für das globale Internetsystem. Es geht darum, immer mehr Server zu verbinden, die Geometrie der Erde aufzugreifen und kurze Verbindungswege zu schaffen. Mit einer hyperbolischen Geometrie auf dem Kreis kann das sehr gut simuliert werden. Da passen (weiter draußen und am Rand) unendlich viele Punkte rein. Also genug Platz für zukünftige Server. Nur diese hyperbolische Geometrie, die macht mir echt zu schaffen. Weiterlesen

Graphische Liebe
Letzte Nacht hatte Rike einen Alptraum: Sie geht auf einem Grat in einem riesigen Gebirge, rechts und links ganz tiefe Schluchten. Dann fällt sie zu der einen Seite und wacht auf. Sie macht sich Sorgen, sie hat Liebeskummer. Sie hat gehört, dass sich Max in Lila verliebt hat. Jetzt überlegt sie, ob sie nach Kalkutta fliegen soll, um mit Max ein paar schöne Tage zu verbringen. Doch wenn sie zu Max fliegt, wird Ben ihr das übelnehmen. Sie hat das Gefühl, sich endgültig einer Seite zuwenden zu müssen, sich somit entscheiden zu müssen.
Jetzt nimmt sie ein Blatt Papier und schreibt die Beziehungssituation graphisch auf. Wenn zwei Menschen zusammenkommen, sich lieben und sich trennen, sieht das graphisch so aus: Weiterlesen

Wie man an Zitronen-Singularitäten scheitert
Jan hat Rike in seinen Garten mit kleinem Gewächshaus eingeladen. Er hat es geschafft, Zitronenbäumchen anzubauen. Er zeigt Rike seine eigenen Zitronen. Sie haben so einen Knick und gehören deshalb nicht in die Gruppe praller Äpfel oder Kirschen. Aber wie klassifiziert man solche Früchte? Weiterlesen

Wie viel Mathematik braucht ein zukünftiger Biologe?
Rike trifft Jan auf einer Geburtstagsparty. Jan möchte gern Biologie studieren, aber er muss wegen des NC noch warten. Auch dieses Jahr hat er noch keinen positiven Bescheid bekommen. Er verbringt viel Zeit im Garten und am PC, doch mit Lehrern kam er nicht so gut klar, so hat er nur ein mittleres Abi geschafft. Er versucht, alle Pflanzen und Tiere, die er kennt, auf seinem PC digital zu katalogisieren. Da trifft es sich gut, dass er Rike trifft. Weiterlesen

Wie Apfelsinen natürlich trianguliert werden
Rike gibt heute eine kleine Party in ihrer neuen Wohnung. Sie bereitet mit Max ein paar Cocktails in der Küchenecke vor. Als sie Zitronen und Apfelsinen aufschneiden, fällt Max die Schönheit der Formen auf. Doch Rike meint, dass ist Effizienz, es ist doch ganz normal, jede Fläche in Dreiecke zu zerlegen. Sie erklärt ihm Triangulierung. Weiterlesen

Horizont als Zufallsweg II
Im Beitrag Horizont als Zufallsweg haben wir geometrische und topologische Eigenschaften der Horizontkurve untersucht. Der Horizont wurde als Weg vom linken zum rechten Bildrand verstanden. Fotografische Eigenschaften (wie Fokus, Auflösung und Objektiv) wirken sich auf die Glattheit der Kurve aus. Alle Beispiele hatten einen zusammenhängenden Weg von 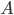
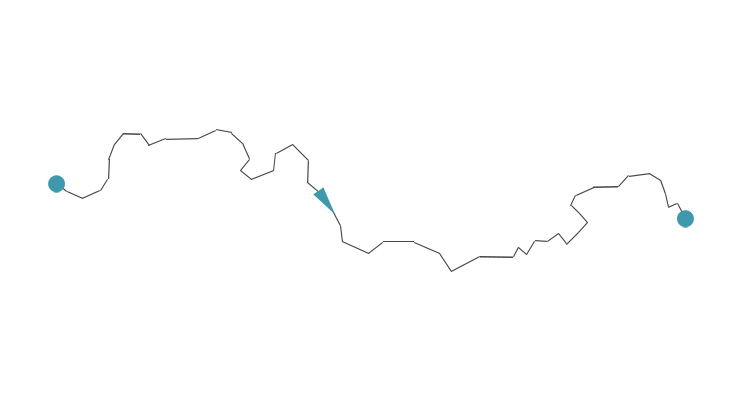
Horizont als Zufallsweg
Überaus leidenschaftlich berichtet Kevin Hartnett in seinem Überblicksartikel A Unified Theory of Randomness von neuen Zugängen zur Beschreibung zufälliger Prozesse. Hartnett schreibt in diesem Artikel über Scott Sheffields neue Theorien zufälliger Wege, Formen und Geometrien. Weiterlesen
