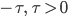Rike trifft Jan auf einer Geburtstagsparty. Jan möchte gern Biologie studieren, aber er muss wegen des NC noch warten. Auch dieses Jahr hat er noch keinen positiven Bescheid bekommen. Er verbringt viel Zeit im Garten und am PC, doch mit Lehrern kam er nicht so gut klar, so hat er nur ein mittleres Abi geschafft. Er versucht, alle Pflanzen und Tiere, die er kennt, auf seinem PC digital zu katalogisieren. Da trifft es sich gut, dass er Rike trifft. Neben den einheimischen Pflanzen und Tieren möchte er zu gern auch die Flora und Fauna der ganzen Welt kennenlernen. Er hat von einer Blume gelesen, deren Frucht verdreht ist, die Blumenbachia Hieronymi. Sie gedeiht in Südamerika. Um sie zu sortieren, muss er nun topologische Eigenschaften von Pflanzenteilen in seine Liste einführen.
Bachiafrucht
Rike Warum fasziniert Dich denn diese Blumenbachia so sehr?
Jan Diese Verdrehung der Frucht gibt es bei uns nicht. Die möchte ich genauer studieren.
Rike Wie sieht denn die Frucht genauer aus?

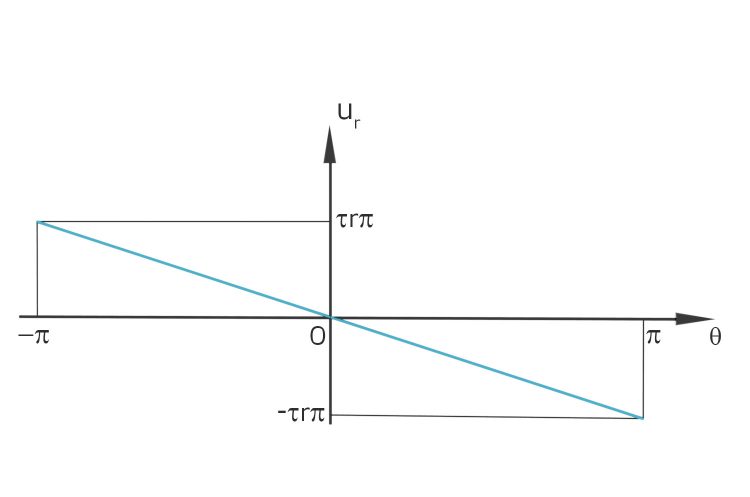
Jan Sie ist ca. 2 cm groß und auch innen verdreht. Ich habe hier ein paar antike Bilder von Ignaz Urban:
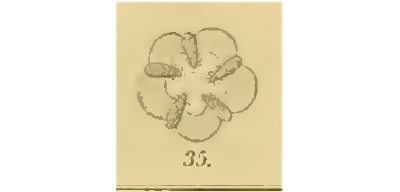

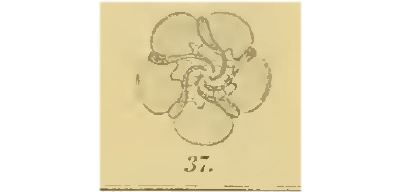
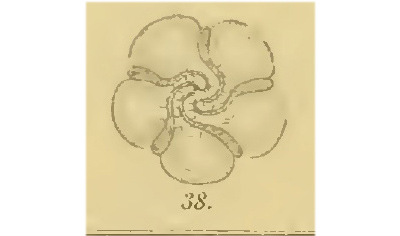
Rike Sag mal, Jan, verstehst Du Latein?
Jan Klar, das brauche ich doch. Ich denke lateinisch und manchmal träume ich auch lateinisch, voll cool.
Rike Okay, Urbans Bilder sehen gut aus, da können wir bei jedem Schnitt in jedem Punkt einen Vektor anbringen, in der Mechanik heißt das, die Torsion bestimmen. In der Mechanik gibt es da Vorbilder.
Jan Ja, das habe ich mir auch schon gedacht....
Torsion eines dünnen Stabes
Rike Das Kalkül geht so: Du stellst die einen dünnen Stab vor, der gleichmäßig verdreht wurde.

Jan Okay.
Rike Zuerst brauchst Du ein Koordinatensystem, zum Beispiel ein kartesisches, mittig im Stab, und in der Höhe, na, sagen wir mal, nehmen wir unten den Nullpunkt.
Die Torsion des Stabes durch äußere Krafteinwirkung erzeugt eine Änderung der Geometrie. Aus einem Punkt P wird ein Punkt P':
Verschiebungsvektor 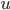
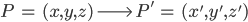
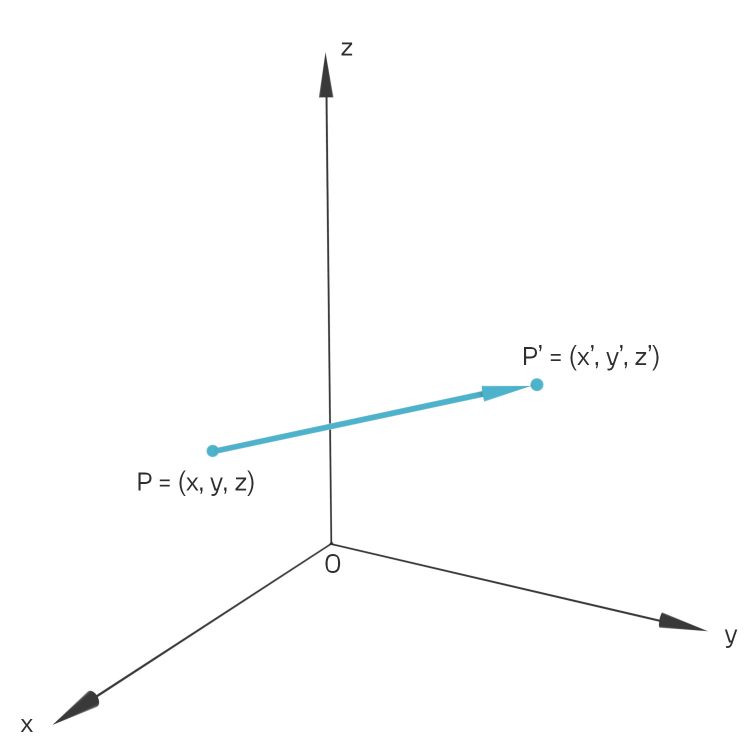
Der Vektor
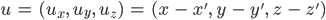
heißt Verschiebungsvektor. Und die Abbildung u von allen Punkten des Stabes
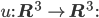
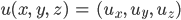
nennen wir mal in unserem Fall Torsionsfeld. An jeden Punkt kannst du den Verschiebungsvektor anheften und bekommst so eine Art Feldlinien.
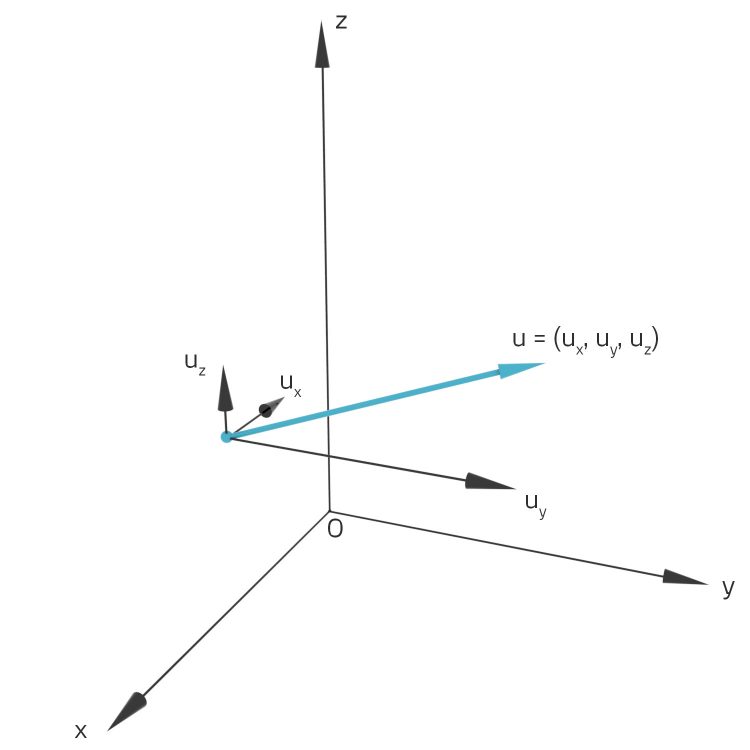
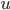
Den Winkel, den ein Punkt P bei der Verdrehung bis zum Punkt P' mit der Höhe 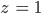 überstreicht, nennt man Torsionswinkel
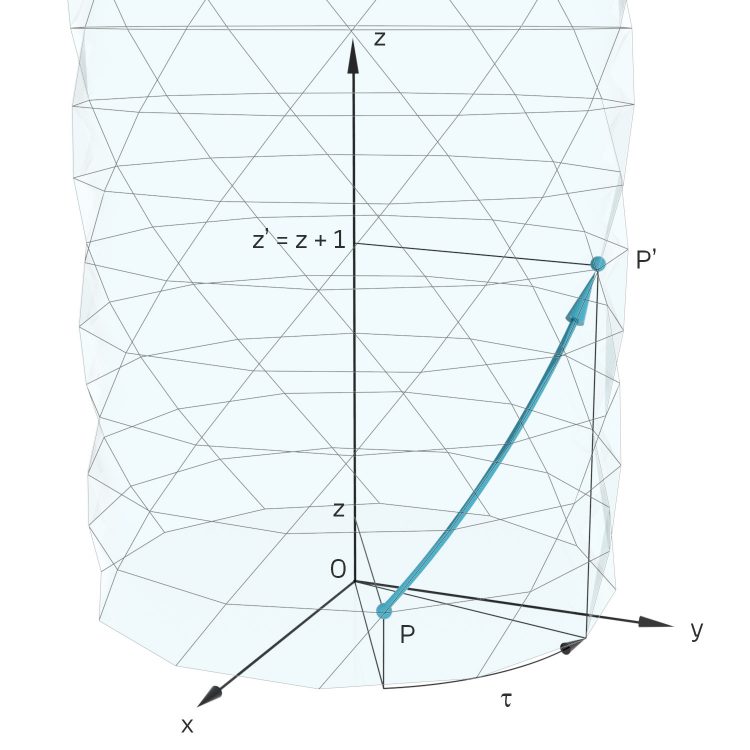
überstreicht, nennt man Torsionswinkel 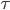 . Das sind nur Bezeichnungen und eine Skalierung.
. Das sind nur Bezeichnungen und eine Skalierung.
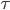
Jan Gut.
Rike Bei einer Torsion eines dünnen Stabes um die z-Achse setzt man:
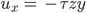
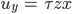
Und erhält für 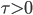 ein solches Feld
ein solches Feld
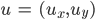
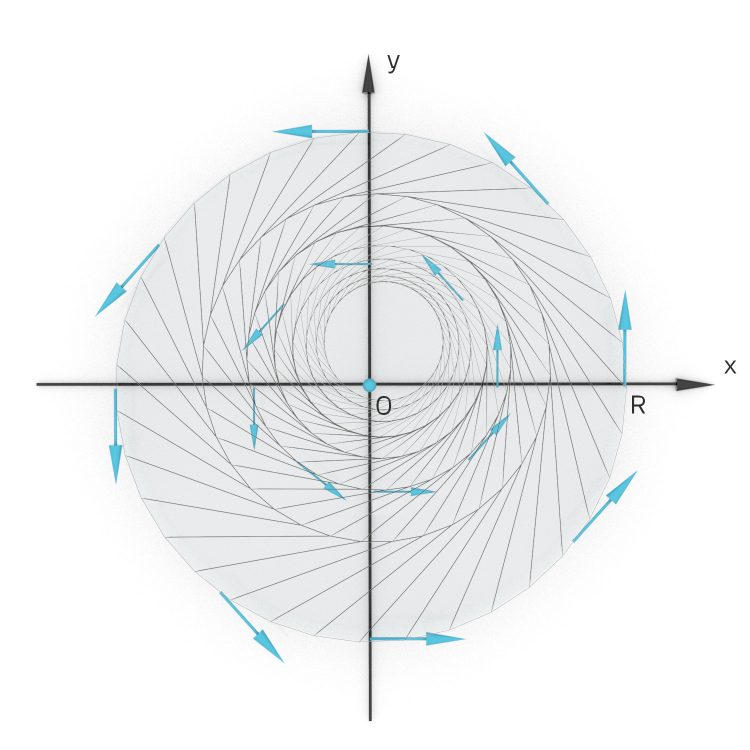
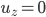 , siehe Landau.
, siehe Landau.Jan Genau, eine Linksdrehung, die brauche ich auch. Das Bild nehmen wir für den Querschnitt durch die Frucht an ihrer breitesten Stelle. Aber Blumenbachia ist kein Stab, Rike.
Torsion der Bachiafrucht
Rike Okay. Dann lass uns Kugelkoordinaten nehmen:
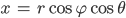
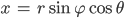
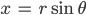
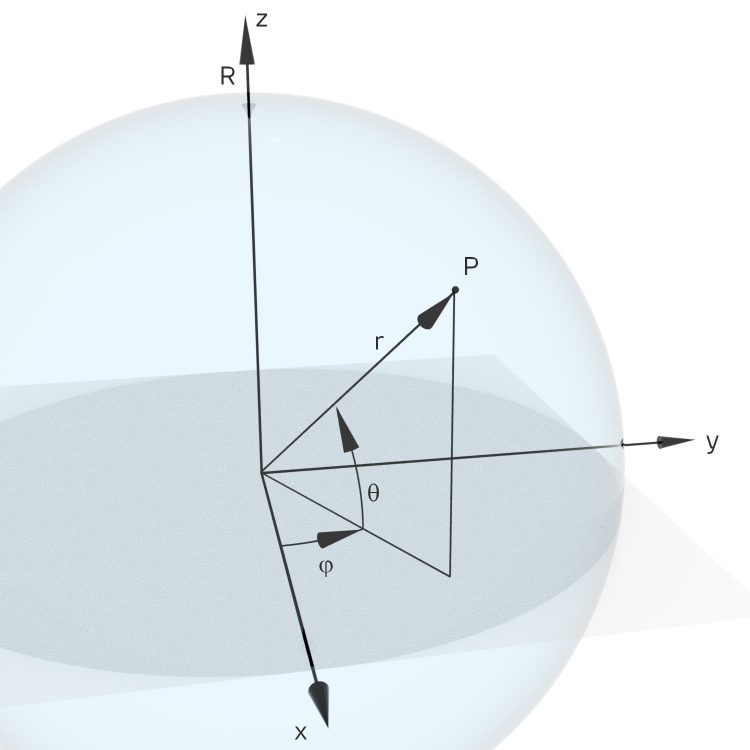
Lass uns das Torsionsfeld in Kugelkoordinaten schreiben, Deine Bachia ist doch recht kugeling?
Jan Haha, die Bachiafrucht ist kugelig.
Rike Gut, dann:
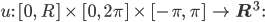
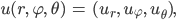
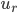 ... radiale Verschiebung,
... radiale Verschiebung,
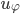 ... Azimutverschiebung,
... Azimutverschiebung,
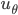 ... Elevationsverschiebung.
... Elevationsverschiebung.
Ich würde das Koordinatensystem in die Mitte der Frucht legen, sodass bei der breitesten Dicke der Nullpunkt ist und 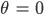 . Da ist der größte Querschnitt. Dort ist die radiale Verschiebung Null.
. Da ist der größte Querschnitt. Dort ist die radiale Verschiebung Null.
Jan Klar! Von da aus deformiert sich die Frucht nach oben und unten, die Querschnitte werden kleiner.
Ansatz für das Torsionsfeld
Rike Richtig. Warte mal, es müsste gar nicht schwer sein, hier,
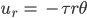
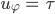
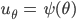
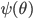 müssen wir noch bestimmen.
müssen wir noch bestimmen.
Jan Was bedeutet das?
Rike Die 2. Gleichung bedeutet, dass jeder Punkt um den Winkel 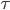 weitergedreht wird.
weitergedreht wird.
Jan Verstehe.
Rike Die erste Gleichung bedeutet, dass der Radius von P zu jedem P‘ sich verkleinert solange 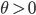 das heißt, die Muster verkleinern sich. Für negative
das heißt, die Muster verkleinern sich. Für negative 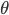 , also unterhalb des Nullpunktes, vergrößert sich der Querschnitt. Am äußeren Radius r = R ist die radiale Deformation am größten, im Nullpunkt am kleinsten.
, also unterhalb des Nullpunktes, vergrößert sich der Querschnitt. Am äußeren Radius r = R ist die radiale Deformation am größten, im Nullpunkt am kleinsten.
Jan Okay!
Rike Die letzte Gleichung beschreibt, wie sich die Elevation 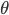 verändert. Was meinst Du?
verändert. Was meinst Du?
Jan In jedem Punkt wird die Elevation größer, sieh Dir doch die Frucht an! Sie ist unten sehr prall, alles drängt nach oben und oben will sie nur noch als Kugel zum Abschluss kommen. Aber wie geht das mathematisch? Unten, bei
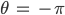
ist 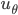 sehr groß gegenüber
sehr groß gegenüber 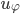 , weiter oben ist es umgekehrt?
, weiter oben ist es umgekehrt?
Rike Jan, Du machst das super! Dann haben wir so einen Verlauf?
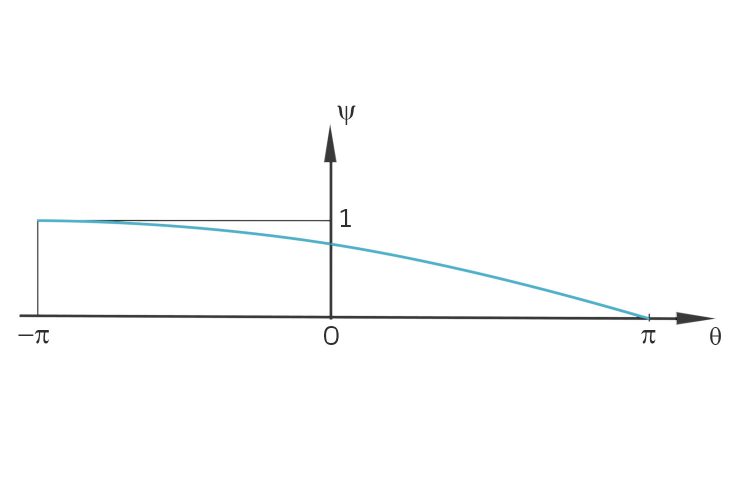
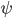 , die Änderung der Elevation in Abhängigkeit vom Elevationswinklet
, die Änderung der Elevation in Abhängigkeit vom Elevationswinklet 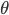
Jan Ja, so ungefähr.
Rike Hm, gut, die Formel findest Du doch?
Jan Hm, ja, ist eine Parabel, nach unten geöffnet, ja, beide Punkte einsetzen…
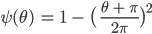
Rike Stimmt. Jetzt haben wir das Feld in einer Näherung gefunden:
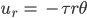
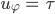
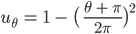
Das ergibt ein schönes Bild:
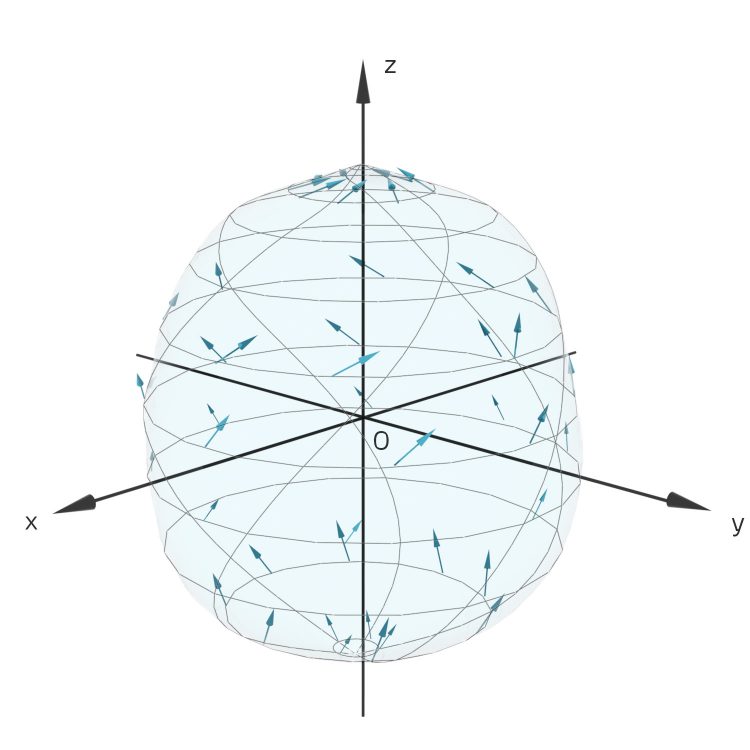
Jan Verstehe! Das passt wirklich gut. Danke, Rike!
Rike Jetzt lass uns Geburtstag feiern!
***
Übungsaufgaben
- Wie sieht ein rechtsdrehendes Feld aus?
- Zeichne
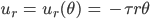
für festes
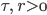 .
.