Max bereitet sich im Trainingslager auf die neue Handballsaison vor. Die Mannschaft macht verschiedene Ballübungen zum Technikaufbau. Eine davon ist ein sogenannter Stemmwurf, wo man den Ball über den oberen Holm eines Stufenbarrens so an eine Wand werfen soll, dass der Ball an dieser Wand abprallt und wieder über denselben Holm zurückfliegt. Sosehr Max sich auch anstrengt, irgendwie gelingt es ihm nicht. Doch als er am Abend eine Zeichnung dazu macht, fällt ihm die Lösung ein.
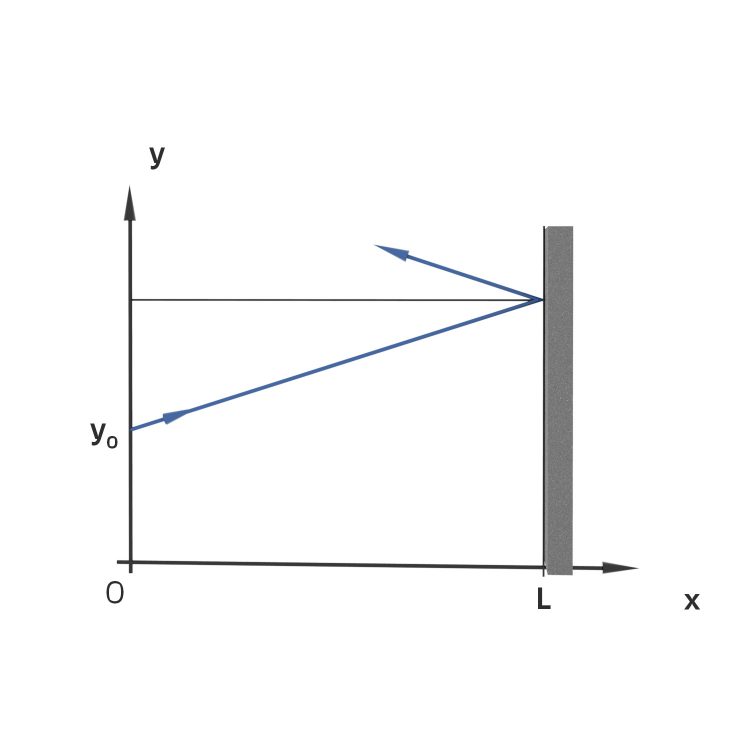
Abprall an der Wand
Max überlegt, wenn er kraftvoll über den oberen Holm an die Wand wirft, müsste der Ball auf jeden Fall nach oben abprallen.
Einfache Physik
Doch irgendwas stimmt nicht. So erinnert er sich an seinen Physikunterricht: Der Ball fällt wegen der Erdbeschleunigung nach unten. Also kriegt er für die y-Koordinate seines Wurfes folgende Gleichung:
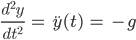
und nach Integration:
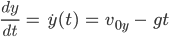
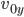
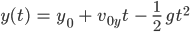
und 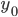
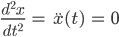
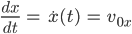
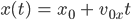
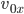
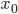
Wenn er das Koordinatensystem so legt, dass bei
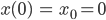
ist, dann hat er die Gleichungen in x- und y-Richtung für einen Wurf:
Zeitabhängige Lösung
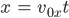
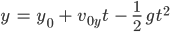
Die erste der beiden kann er gut nach t umstellen und in die zweite einsetzen:
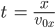
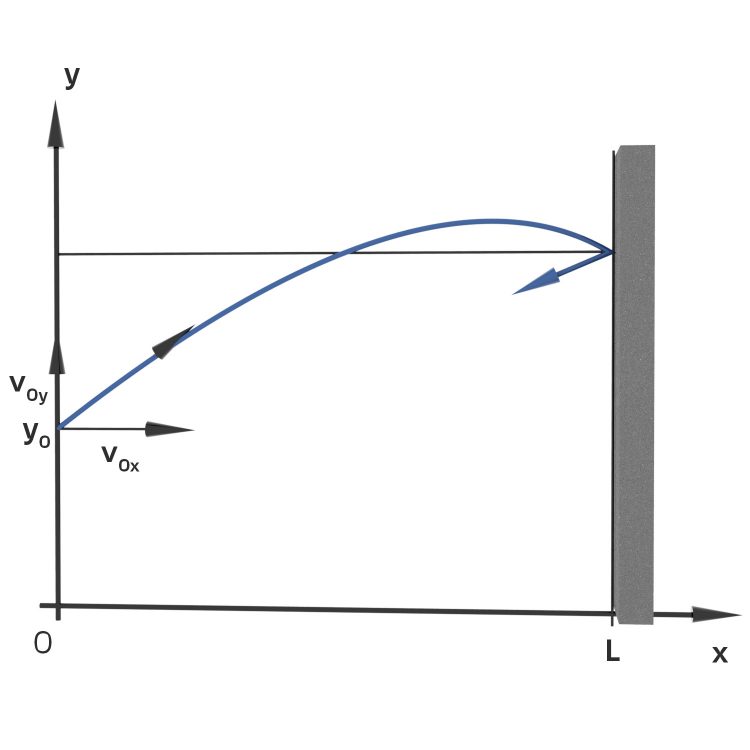
Parabel in x-y-Koordinaten
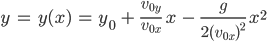
Als er das dann zeichnet, merkt er, dass es eine Parabel ist:
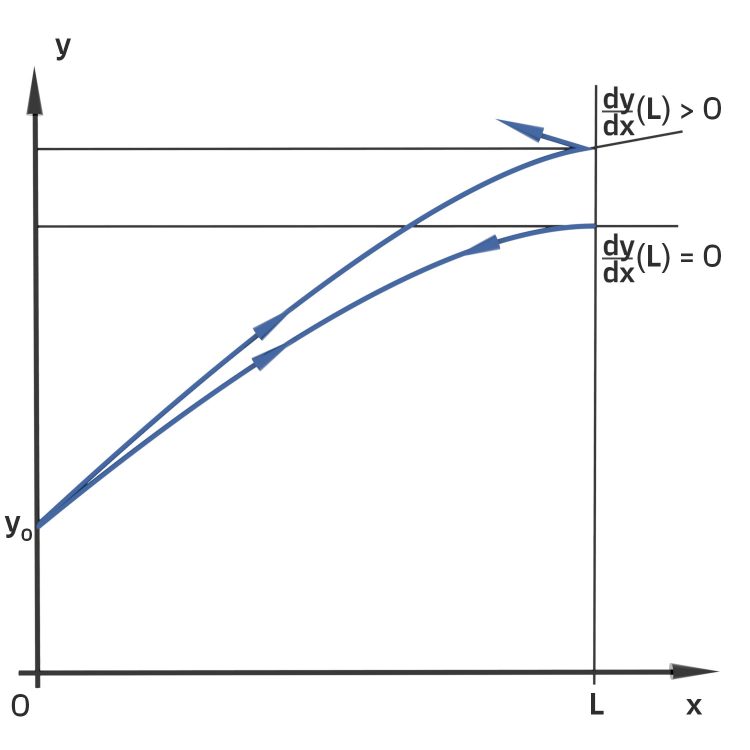
Wand-Rand-Bedingungen
Und er sieht auch, dass der Abprall bei
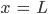
durchaus nach unten gerichtet sein kann, so wie er es erlebt hat. Doch was kann er tun? Er muss so werfen, dass der Ball waagerecht oder nach oben abprallt:
Das ist gerade die Bedingung
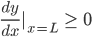
Das versucht er an der Parabel:
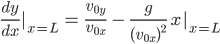
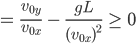
Und das ist genau dann erfüllt, wenn
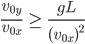
oder genau dann, wenn
Finale Bedingung
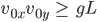
Aha, er muss sowohl nach vorn als auch nach oben mit Power werfen, wenn er den besten Abwurfwinkel von 45° wählt:
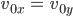
und
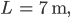
dann wären das
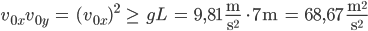
und
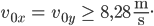
Das müsste doch zu schaffen sein!
***
Übungsaufgaben
- Welche Anfangsgeschwindigkeiten braucht man für a) L = 10 m oder b) L = 3 m?
- Kann Max auf das Gleichheitszeichen in der finalen Bedingung hoffen?
Lösungen
- a)
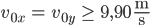
b)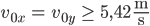
- Nein, unter realistischen Bedingungen wird der Ball nicht mit der derselben Geschwindigkeit abprallen wie er auftrifft. Das geschieht in Abhängigkeit von den Eigenschaften des Balles und der Wand. Ein gewisser Verlustfaktor muss einbezogen werden.