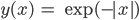Jan hat Rike in seinen Garten mit kleinem Gewächshaus eingeladen. Er hat es geschafft, Zitronenbäumchen anzubauen. Er zeigt Rike seine eigenen Zitronen. Sie haben so einen Knick und gehören deshalb nicht in die Gruppe praller Äpfel oder Kirschen. Aber wie klassifiziert man solche Früchte?
Zitronen
Jan Guck mal Rike, fast gar kein‘ Unterschied ...
Rike ... hahaha, Du bist ja total verrückt, hahaha, die Zitronen sind doch gar nicht so rund wie deine Brille ... sorry aber da gehen gleich meine mathematischen Sensoren an, hahaha…
Jan Okay, die Zitronen sind nicht so verdreht wie die Blumenbachia, hier können wir kein Torsionfeld aufstellen.
Rike Oh, Jan, viele Mathematiker würden sich freuen, wenn sie so eine Zitrone von Dir kriegen könnten. Endlich mal ein nichttriviales Beispiel...
Jan Wovon redest Du?
Tangentialebenen an Zitronen
Rike Man könnte versuchen, Deine Zitrone wie die Erde zu behandeln. Wie ein Globus! Von jedem Gebiet fertigst Du eine Karte an – also einen ebenen Atlas. Das geht überall ganz gut, nur an dieser Kurve C klappt das nicht.
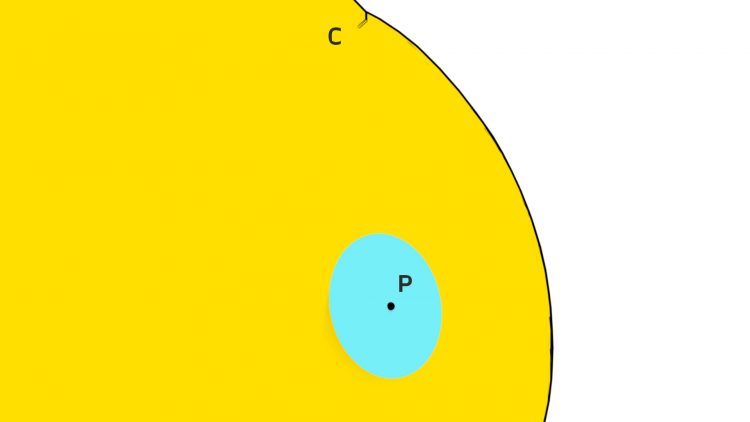
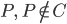
Jan Wie – das klappt nicht? Wir können doch hier in der Kurve C am Punkt Q von der einen Seite eine Karte 'ranquetschen und von der anderen Seite eine andere.
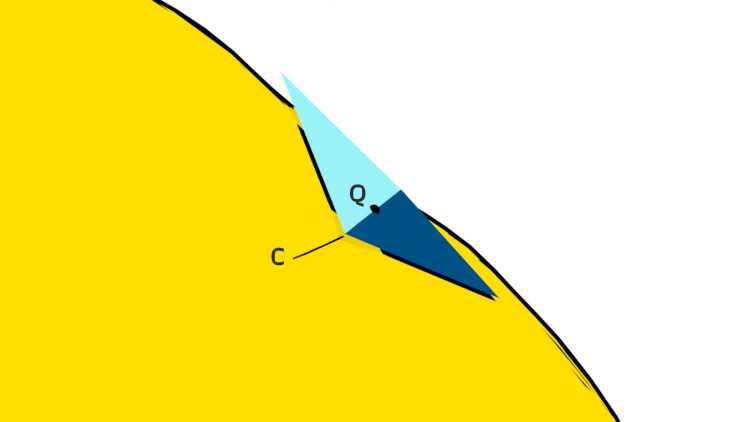
Rike Stimmt. Dann hast Du zwei Karten, die sich nicht überlappen, Q liegt auf dem Rand jeder Karte. Das ist so in der Theorie der Mannigfaltigkeiten nicht vorgesehen. Die mathematischen Karten haben keinen Rand. Ein Karte, wo Q innen liegt, kriegst Du nur als stetige Abbildung in den R² hin, aber nicht als überall differenzierbare.
Jan Ich hatte in der Schule noch nie eine nicht differenzierbare Funktion. Wir hatten Polynome, die Exponentialfunktion, rationale Funktionen ...
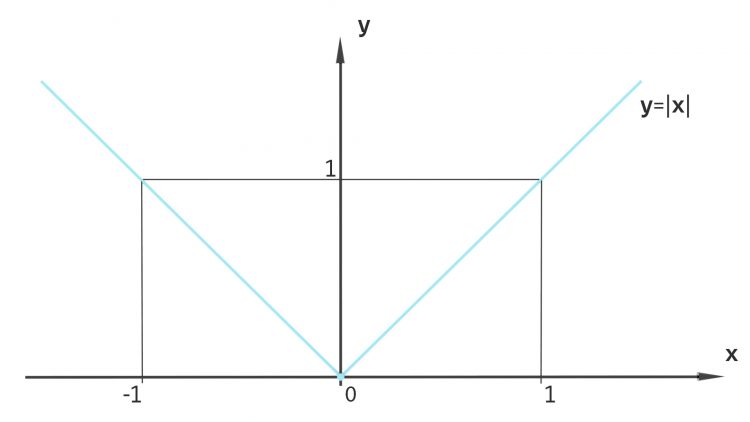
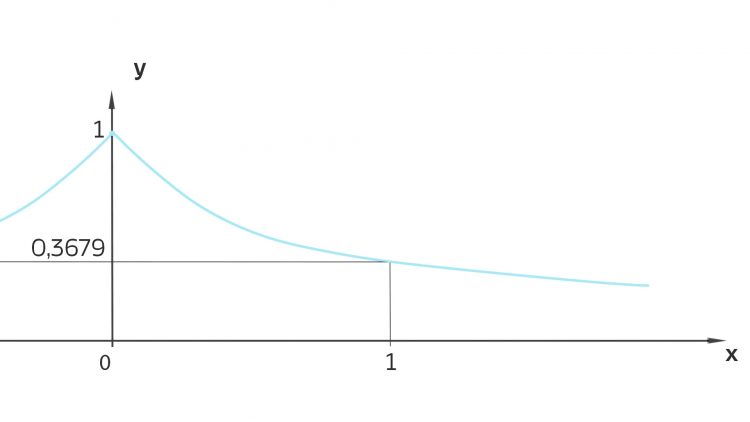
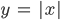 ist in
ist in 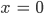 nicht differenzierbar.
nicht differenzierbar.
Rike So eine nicht differenzierbare Stelle hast Du bei der Betragsfunktion. Da hast Du von links an der Stelle 0 die Ableitung -1 und von rechts die Ableitung +1. Und weil die beiden Werte verschieden sind, ist die Betragsfunktion an der Stelle x = 0 nicht differenzierbar.
Jan Na gut. Ist das nicht traurig, wenn da diese Minimax-Aufgaben nicht funktionieren? Der Betrag hat ja gerade in 0 sein Minimum!
Rike Stimmt. Du musst die nicht differenzierbaren Stellen immer extra betrachten.
Jan Und wie geht das bei meiner Zitrone?
Rike Ich würde sagen, wegen dieser Kurve C ist Deine Zitrone eine nicht differenzierbare Mannigfaltigkeit.
Zitronen-Singularitäten-Entfernungsidee
Wenn wir die Punkte dieser Kurve C einfach 'rausnehmen und sie da ein bisschen aufbiegen, natürlich differenzierbar, kriegen wir eine Art Kugel mit Loch.
Und weil der Rand C des Loches nicht dazugehört – den haben wir ja entfernt – kannst Du an jeden Punkt P der Zitrone eine Tangentialebene legen, auch ganz nahe bis zum Rand.
Jan Du machst aus meinen Zitronen so eine Art ausgehöhlten Kürbis?
Rike Ja, eine differenzierbare Mannigfaltigkeit!
Jan Nein, das geht nicht! Ich protestiere! Meine Zitronen bleiben so wie sie sind. Kein Mathematiker macht da Kürbisse draus, auch Du nicht, Rike.
Rike Mann, jetzt bin ich mit meiner Zitronen-Singularitäten-Entfernungsidee gescheitert! Mist. Was nun?
Jan Wenn Du Lust hast, ich habe für uns einen ganz besonderen Cocktail vorbereitet – mit Zitronen und Zutaten nur aus meinem Garten!
Rike Dann lass uns mal probieren!
***
Übungsaufgaben
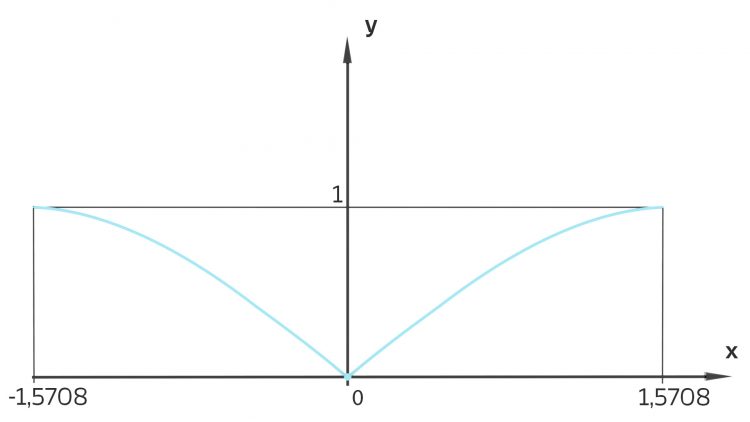
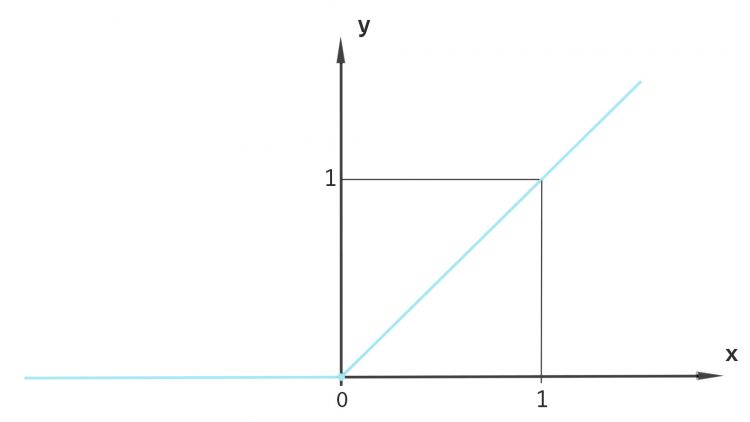
Wie können folgende Funktionen formuliert werden?