Max trainiert weiterhin Handball im Trainingslager. Er macht diese tolle Übung, wo er mit einer Hand einen Luftballon immer nach oben stupst und mit der anderen Hand einen Handball auf der Stelle dribbelt. Es ist ziemlich anstrengend, keinen runter fallen zu lassen. Er stellt fest, dass es einfacher geht, wenn er den Luftballon im „Einklang“ mit dem anderen Ball anregt. Am Abend überlegt er sich die Formeln dazu.
Luftballon
Zuerst überlegt er, wie der Luftballon fliegt. Er wird von der Höhe 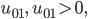 nach oben mit einer Anfangsgeschwindigkeit von
nach oben mit einer Anfangsgeschwindigkeit von 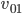 gestupst,
gestupst, 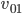 soll eine positive Zahl sein. Die Erdbeschleunigung g sorgt dafür, dass der Luftballon wieder nach unten kommt. Es sind dieselben Gesetze wie bei der Stufenbarren-Wurfübung.
soll eine positive Zahl sein. Die Erdbeschleunigung g sorgt dafür, dass der Luftballon wieder nach unten kommt. Es sind dieselben Gesetze wie bei der Stufenbarren-Wurfübung.
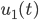 des Luftballons.
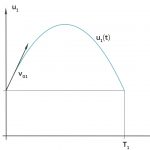
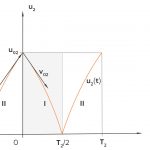
des Luftballons.Wenn Max mit 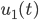 die Höhe des Luftballons in Abhängigkeit von der Zeit bezeichnet, dann wird die Kurve schnell klar:
die Höhe des Luftballons in Abhängigkeit von der Zeit bezeichnet, dann wird die Kurve schnell klar:
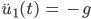
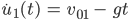
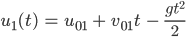
Für die Zeiten 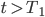 muss er die Kurve einfach verschieben:
muss er die Kurve einfach verschieben:
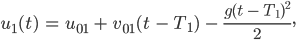
für 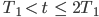 usw.
usw.
Der Luftballon fällt natürlich nicht beliebig nach unten, denkt Max, sondern nur bis zur Höhe 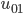 . Dort wird er wieder nach oben gestupst. Das ergibt
. Dort wird er wieder nach oben gestupst. Das ergibt
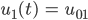
genau dann, wenn
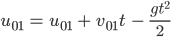
also, wenn
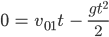
oder
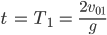
Das ist genau die die Zeitdauer einer Periode für den Luftballon. Das ging ja ganz gut. Jetzt der Handball!
Handball, Fall I
Der Handball wird von der Höhe 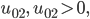 nach unten mit der Geschwindigkeit
nach unten mit der Geschwindigkeit 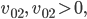 geprellt und in der Höhe
geprellt und in der Höhe 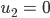 reflektiert. Wie auch beim Luftballon haben wir die Erdbeschleunigung zu berücksichtigen.
reflektiert. Wie auch beim Luftballon haben wir die Erdbeschleunigung zu berücksichtigen. 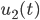 soll die Höhe des Handballs in zeitlicher Abhängigkeit beschreiben. Max merkt schon, dass es etwas komplizierter ist. Er fängt mit dem Fall I an, in dem er den Ball prellt bis der Ball den Boden berührt. Hier gilt:
soll die Höhe des Handballs in zeitlicher Abhängigkeit beschreiben. Max merkt schon, dass es etwas komplizierter ist. Er fängt mit dem Fall I an, in dem er den Ball prellt bis der Ball den Boden berührt. Hier gilt:
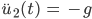
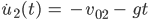
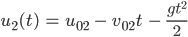
für 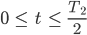 .
.
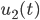 .
.Wie groß ist die Periode 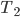 ? Das geht wie beim Luftballon. Max berechnet die halbe Periode
? Das geht wie beim Luftballon. Max berechnet die halbe Periode 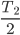 , das ist genau dann, wenn der Handball den Boden berührt:
, das ist genau dann, wenn der Handball den Boden berührt:
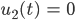
genau dann, wenn
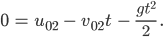
Beide Seiten mit 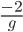 multipliziert ergibt
multipliziert ergibt
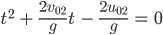
Jetzt kann er die p-q-Formel benutzen, die ihm Rike vor langer Zeit beigebracht hat, und kriegt
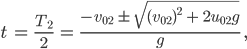
oder
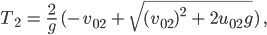
weil 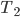 nur als positive Zahl in diesem Zusammenhang Sinn macht, lässt er das Minus weg. Soweit, so gut. Doch wie soll er das für die Reflexion machen?
nur als positive Zahl in diesem Zusammenhang Sinn macht, lässt er das Minus weg. Soweit, so gut. Doch wie soll er das für die Reflexion machen?
Handball, Fall II
Am einfachsten wäre es doch, den Fall II für 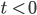 zu betrachten. Wenn die Energieerhaltung gilt, bei einem idealen Ball zunächst mal, dann hat er bei
zu betrachten. Wenn die Energieerhaltung gilt, bei einem idealen Ball zunächst mal, dann hat er bei 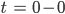 ebenso die Geschwindigkeit
ebenso die Geschwindigkeit 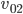 , nur mit einem anderen Vorzeichen:
, nur mit einem anderen Vorzeichen:
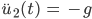
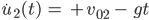
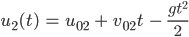
für 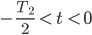 . Über diese Zeiten hinaus muss Max die Kurve
. Über diese Zeiten hinaus muss Max die Kurve 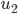 um
um 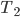 oder Vielfache von
oder Vielfache von 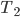 verschieben.
verschieben.
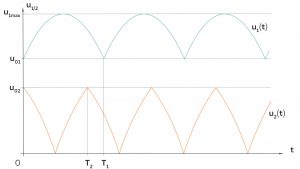
„Einklang" der Bewegungen
Als Max beim Training auf gut Glück probiert hat, kam keine regelmäßige Bewegung beider Bälle zustande. So wäre es doch gut, denkt er sich, wenn die beiden Perioden Vielfache voneinander wären:
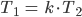
k … ganze, positive Zahl. In diesen Ansatz setzt er einfach die Formeln für 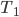 und
und 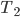 ein und erhält
ein und erhält
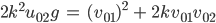
Von all den Parametern kann Max am einfachsten (in der Praxis) 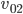 bestimmen und stellt die Formel nach
bestimmen und stellt die Formel nach 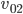 um. Weil
um. Weil 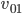 auf jeden Fall größer Null ist, bekommt er nach Division durch
auf jeden Fall größer Null ist, bekommt er nach Division durch 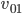 :
:
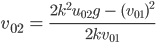
Der Zähler ist positiv, falls
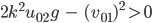
oder
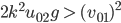
oder
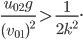
Für Max ist
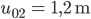
und
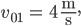
also
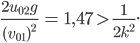
Also kann Max 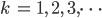 wählen. Er nimmt
wählen. Er nimmt
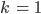
und erhält damit
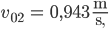
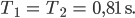
Das ergibt folgendes Bild:
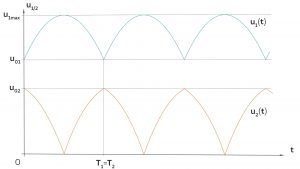
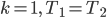
Das ist doch eine supereinfache Lösung, das lässt sich machen, denkt Max und freut sich auf morgen. Da fällt ihm ein, dass Überlagerungen von Schwingungen schöne Muster ergeben, sogenannte Lissajous-Figuren. Das will er dann auch noch ausprobieren.
***
Übungsaufgaben
Zeichne die Lissajous-Figuren 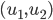 für einen Fall
für einen Fall 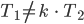 und für den Fall
und für den Fall 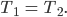
Lösungen

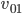 = 4 m/s,
= 4 m/s, 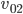 = 2,1 m/s.
= 2,1 m/s.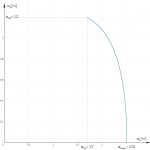
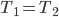 mit den oben verwendeten Werten.
mit den oben verwendeten Werten.