Rike hat letzte Nacht Folgendes geträumt:
Sie liegt im Bett. Mehrere Männer fliegen um sie herum und versuchen sie zu schwängern. Die Zeit vergeht, ihr Bauch wölbt sich, sie bekommt ein Mädchen. Dann fliegen wieder Männer heran, sie wird wieder schwanger. Diesmal ist es ein Junge, doch der ist tot. Sie weint bitterlich, doch es bleibt ihr keine Zeit zur Trauer. Sie wird wieder schwanger. Nun sterben auch die Väter einer nach dem anderen nach kurzer heftiger Krankheit. Hochschwanger pflegt sie die sterbenden Väter, die nun nicht mehr fliegen können und in Rikes Bett liegen. Sie kann nicht mehr und schreit um Hilfe.
Sie erwacht von ihrem eigenen Schrei. Schweißgebadet steht sie auf. Sie beruhigt sich, es war nur ein Traum. Dann schaut sie nochmals in den Nature-Artikel, in dem sie gestern von dem Problem gelesen hat und entwickelt ein Modell dafür. Sie will wissen, wie lange sie leben wird.
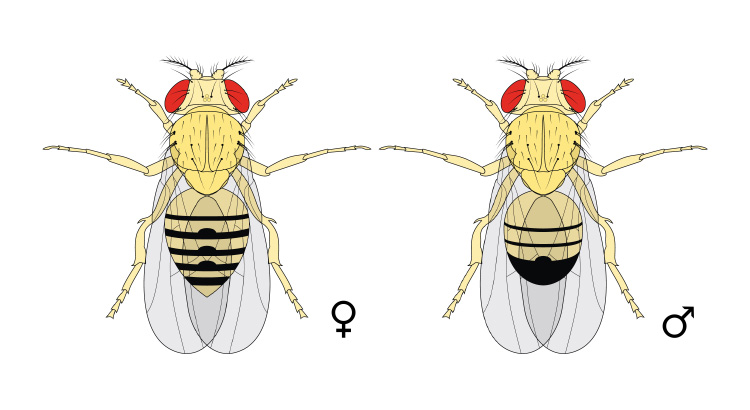
Der Nature-Artikel Male-killing toxin in a bacterial symbiont of Drosophila berichtet über ein außergewöhnliches Naturereignis: Ein endosymbiotisches Bakterium befällt Taufliegen. Dabei sterben sowohl die männlichen, infizierten Taufliegen als auch die männlichen Embryonen (Larven). Toshiyuki Harumoto und Bruno Lemaitre konnten den genauen biochemischen Vorgang der Infektion, der Krankheitsübertragung und des Sterbens analysieren, reproduzieren und erklären.
Diskretes Modell
Rike denkt sich dafür ein diskretes Modell aus.
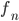 ... Anteil der männlichen Taufliegen zur Zeit n (n-te Fortpflanzungseinheit)
... Anteil der männlichen Taufliegen zur Zeit n (n-te Fortpflanzungseinheit)
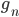 ... Anteil der männlichen Embryonen/Larven zur Zeit n
... Anteil der männlichen Embryonen/Larven zur Zeit n
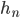 ... Anteil der weiblichen Taufliegen zur Zeit n (n-tes Fortpflanzungseinheit)
... Anteil der weiblichen Taufliegen zur Zeit n (n-tes Fortpflanzungseinheit)
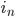 ... Anteil der weiblichen Embryonen/Larven zur Zeit n
... Anteil der weiblichen Embryonen/Larven zur Zeit n
So kann die Anzahl der männlichen Taufliegen nach einer Fortpflanzungsperiode berechnet werden aus dem Anteil der noch lebenden Taufliegen und denen, die nun erwachsen sind:
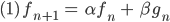
Und die männlichen Embryonen im nächsten „Jahr“ sind so viele, wie noch leben (mit demselben Faktor  wie bei den Erwachsenen, der wird später sehr klein werden, wenn das Bakterium arbeitet) und dazu kommen neu gezeugte, die von der Anzahl der männlichen und weiblichen Fliegen abhängen:
wie bei den Erwachsenen, der wird später sehr klein werden, wenn das Bakterium arbeitet) und dazu kommen neu gezeugte, die von der Anzahl der männlichen und weiblichen Fliegen abhängen:
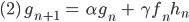
Genauso schreibt sie das für die weiblichen Fliegen und Larven auf:
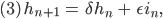
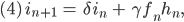
alle Parameter 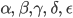 sind nicht negativ und nicht größer als 1:
sind nicht negativ und nicht größer als 1:
Gleichgewichtszustände GGZ
Rike fragt sich, ob es Gleichgewichtszustände für dieses System gibt. Na klar, denkt sie,
ist einer, der triviale. Okay, sonst noch was?
Sie überlegt, wenn sie für einen möglichen GGZ
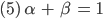
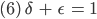
setzt, das bedeutet, dass pro Zeiteinheit der Anteil der Embryonen plus der jetzt erwachsen gewordenen konstant bleibt, das gilt für männliche und weibliche Spezies, dann wäre das doch ganz vernünftig. Für einen möglichen GGZ benutzt sie außerdem die Bezeichnungen
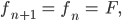
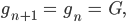
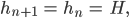
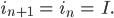
Aus den Gleichungen (1)-(4) werden dann
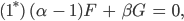
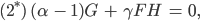
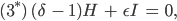
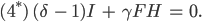
Aus der Gleichung (3*) folgt sofort mit
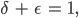
dass
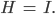
Die Nichtlinearität 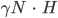 tritt identisch auf und kann aus einer Gleichung eliminiert werden. Nach ein paar Umformungen erhält Rike
tritt identisch auf und kann aus einer Gleichung eliminiert werden. Nach ein paar Umformungen erhält Rike
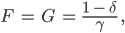
und schließlich
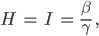
dazu muss 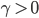 sein.
sein. 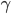 beschreibt die Fortpflanzungsfähigkeit. So hat das diskrete Modell (1)-(6) 2 GGZ, prima, denkt Rike. Wenn sie die Anfangswerte geschickt wählt, nämlich genau im GGZ, dann bleibt das System im GGZ:
beschreibt die Fortpflanzungsfähigkeit. So hat das diskrete Modell (1)-(6) 2 GGZ, prima, denkt Rike. Wenn sie die Anfangswerte geschickt wählt, nämlich genau im GGZ, dann bleibt das System im GGZ:
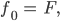
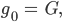
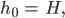
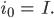
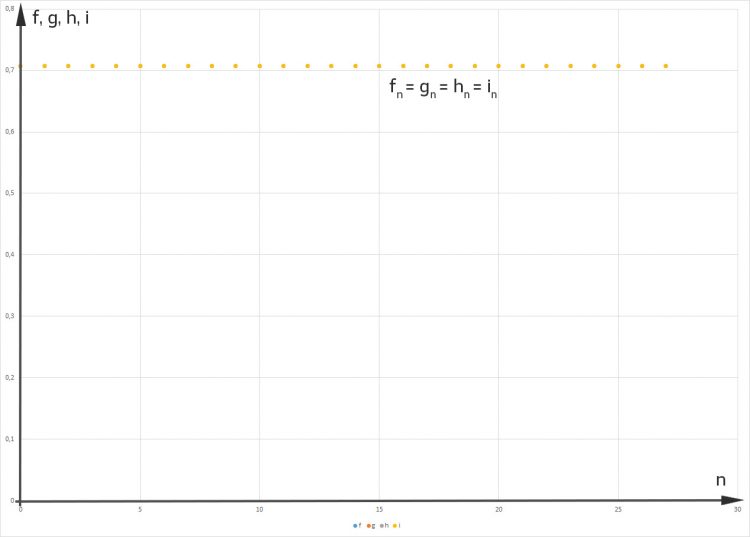
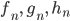 und
und 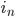 sind gleich (0,707),
sind gleich (0,707), 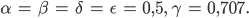
Rikes Modell beschreibt gut das Verhalten gesunder Taufliegen in einer stabilen Population.
Tödliche Krankheit
Sind nun die Taufliegen von dem Bakterium befallen, dann bleiben pro Zeiteinheit nur wenige männliche Spezies 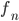 und
und 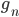 übrig, also ist
übrig, also ist  sehr klein:
sehr klein:

Die Bedingung
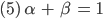
für den GGZ wird nun nicht erfüllt sein, denn es werden sehr wenige männliche Fliegen erwachsen: aus (5) wird
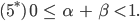
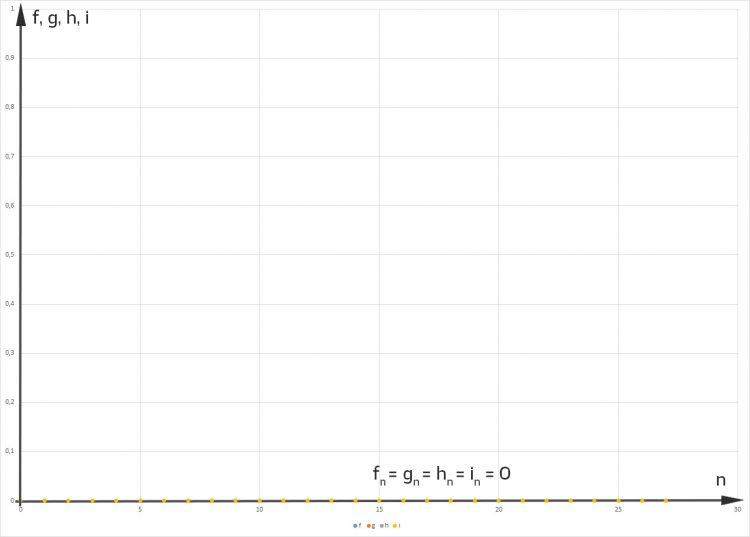
Dann ist das Gleichgewicht gestört. Selbst wenn sie den „Männern“ am Anfang einen Vorsprung gibt:
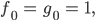
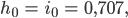
dann gibt es nach ca. 6 „Fortpflanzungsjahren“ doppelt so viele „Frauen“ wie „Männer“ und nach 27 „Jahren“ bleibt als letzte noch messbare Größe nur noch
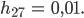
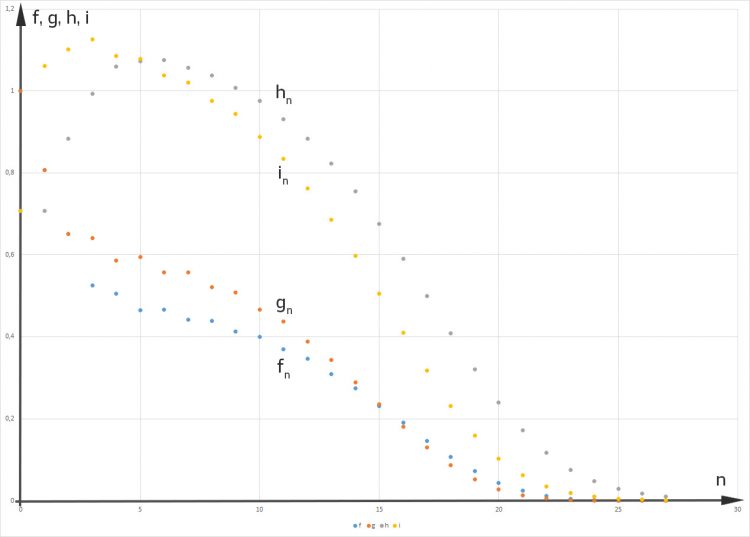
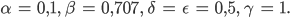
Hmm, ist doch okay, denkt Rike. Außerdem freut sie sich über diesen interessanten Raum mit 4 Veränderlichen und 5 Parametern. Das ist gut.
***
Übungsaufgaben
- Überprüfe den nichttrivialen GGZ!
- Was passiert für
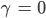 ?
?
Lösungen
2. Für 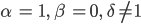 gibt es zwei Scharen von nichttrivialen GGZs:
gibt es zwei Scharen von nichttrivialen GGZs:
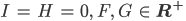
und für 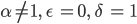 gibt es weitere Scharen von nichttrivialen GGZs:
gibt es weitere Scharen von nichttrivialen GGZs: