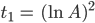Rike trifft sich mit ihrer Schwester Jule in Bielefeld. Jule hat Semesterferien. Sie gehen ins Kino und schauen sich BlacKkKlansman von Spike Lee an. Nach dem Kino schauen sie noch von der Dachterrasse über Rikes Apartment auf das nächtliche Bielefeld. Sie diskutieren, ob der Film Spike Lees Schaffenshöhepunkt ist.
Rike Da fällt mir eine Studie aus Nature ein. Da werden die Schaffenshöhepunkte von Künstlern, Filmemachern und Wissenschaftlern verglichen.
Jule Wie geht denn das?
Filmemacher*innen, Künstler*innen und Wissenschaftler*innen
Rike Warte mal, ja, hier, na klar geht das, die Autoren haben die künstlerischen Arbeiten nach ihren Preisen, die wissenschaftlichen Arbeiten nach dem Rang des Journals und ihren Zitaten und die Filme nach ihren Kritiken und Auszeichnungen bewertet. Es sieht ganz rational und transparent aus.
Jule Na gut.
Rike Und das erstaunliche Ergebnis ist, dass ein "normaler" Wissenschaftler eine Produktivität hat, die der Gleichverteilung ähnelt, ein „normaler" Künstler oder Regisseur ebenfalls. Doch die Genies haben zwar eine gleichmäßige Schaffenskraft (bzgl. der Zeit) aber eine sehr ungleichmäßige Produktivität, was die Werte, Bewertungen oder Preise ihrer Arbeiten angeht. Das ist für Wissenschaftler, Künstler und Regisseure gleich.
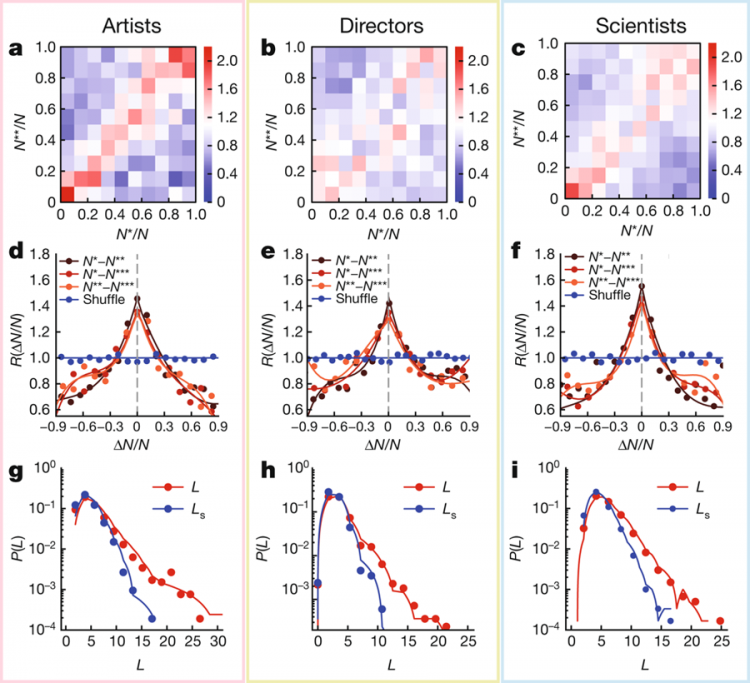
Jule Was? Die Filmemacher haben ihren Karrierehöhepunkt ähnlich wie Wissenschaftler oder Künstler? Hmmm. Wird man denn nicht immer berühmter und immer besser?
Rike Nein, eben nicht, die ganz Großen haben Höhepunkte, und dann ist das vorbei, ihre Leistung sinkt sogar unter die von normalen.
Jule Wenn das schon statistisch ausgewertet wurde, dann können wir beide uns doch mal analytisch ranmachen und versuchen, eine Funktion für diese Höhepunkte zu finden, ja?
Rike Jetzt?
Jule Jetzt hast Du mich neugierig gemacht, jetzt lass uns das probieren. Ich habe eine kleine Anwendung programmiert, wo ich schnell Kurven zeichnen kann.
Rike Okay! Die Normierung ist so, dass die „Normalos“ für alle Zeiten t die Werte 1 bekommen und die Stelle des Höhepunktes bei den Genies hat Lu Liu auf
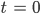
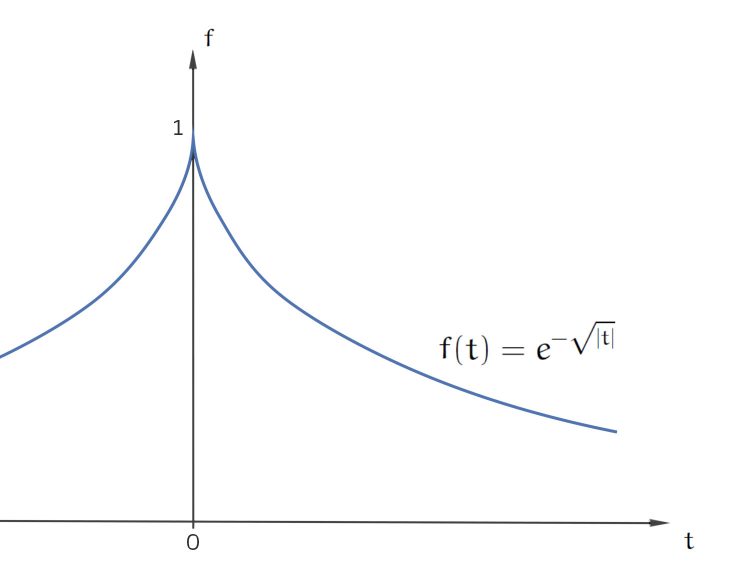
gelegt. Für mich ist das Wichtigste, dass die Funktion
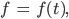
die wir suchen, unbedingt in t = 0 einen steilen Anstieg hat, so steil, wie es geht.
Jule Dann kommt sowas wie die Gauß-Kurve nicht in Frage?
Die Geniekurve
Rike Nee, aber wie wäre es mit
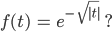
Jule Nicht schlecht, da hast Du Deinen steilen Anstieg. Das Maximum in der Nature-Kurve ist bei ca.
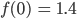
Diesen Wert stecken wir in eine Konstante
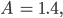
das programmiert sich besser, wenn wir noch mehr untersuchen wollen.
Rike Okay. Also besser wäre
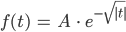
Jule Sag mal, können wir nicht eine Kurvenschar konstruieren, von einem Parameter abhängig, sodass die Kurve der Genies stetig in die Kurve der Normalos übergeht?
Rike Sag mal, bist Du verrückt? Genies werden in Normalos transformiert, Normalos werden in Genies transformiert?
Jule Haha. Weißt Du, es ist doch
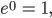
das ist doch genau die Normalo-Verteilung, da brauchen wir doch nur den Parameter in den Exponenten zu stecken, und für den Faktor A ebenso, der soll ja auch 1 werden:
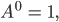
stimmt’s?
Die Genie-Normalo-Kurvenschar
Rike Du bist ja ziemlich clever, also
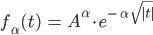
Jule Jawoll,  geht von 0 bis 1. Warte, das zeichne ich mal. Ist ein bisschen schwierig, die Ecke bei Null hinzukriegen und die anderen Kurvenpunkte glatt zu zeichnen. O Shit, jetzt habe ich unendlich viele Alphas zugelassen! Wie viele Alphas soll ich nehmen?
geht von 0 bis 1. Warte, das zeichne ich mal. Ist ein bisschen schwierig, die Ecke bei Null hinzukriegen und die anderen Kurvenpunkte glatt zu zeichnen. O Shit, jetzt habe ich unendlich viele Alphas zugelassen! Wie viele Alphas soll ich nehmen?
Rike Naja, 0, 1, 1/2 ...
Jule Okay, … hier!
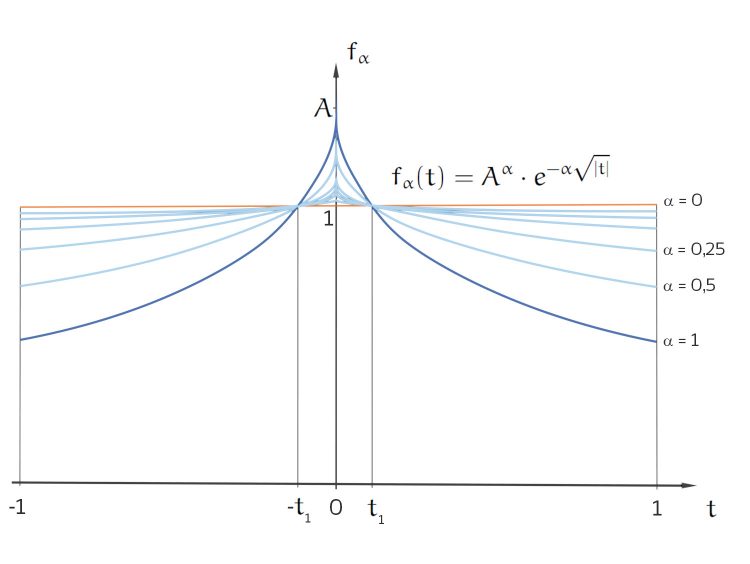
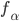 für
für  = 0, 0.03125, 0.0625, 0.125, 0.25, 0.5 und 1.
= 0, 0.03125, 0.0625, 0.125, 0.25, 0.5 und 1.
Rike Wenn Du so weiter machst, wirst Du auch noch ein Genie!
Jule Hahaha
***
Übungsaufgabe
Begründe, dass sich die Kurven für verschiedene Alphas in zwei Punkten 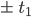 schneiden! Kann
schneiden! Kann 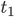 analytisch berechnet werden?
analytisch berechnet werden?
Lösung
Ja,