Wie der Matthäus-Effekt beim Handball funktioniert

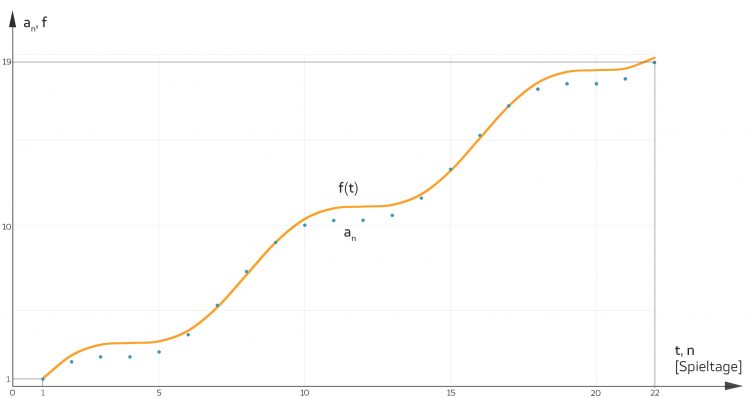
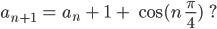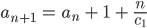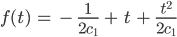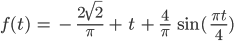Jule und Rike haben Max die Genie-Normalo-Kurve geschickt. Schade, dass er nicht mit ins Kino konnte und auch nicht auf der Dachterrasse sein konnte. Doch beim Handball ist das ganz anders, denkt er. Hier gilt nämlich das Matthäus-Prinzip: Wer gut spielt, wird immer besser, wer nicht gut spielt, hat wenig Chancen. So hat seine Mannschaft die 22 Spieltage der Bundesliga A-Jugend gut geplant. Das erste Spiel hat Max' Mannschaft HSG Handball Lemgo gegen die SG Menden Sauerland Wölfe gewonnen, er hat 1 Tor geworfen.

Rekursive Folge für Handball-Torwürfe

Max denkt, wenn ich bei jedem Spiel ein Tor mehr werfe und noch eine positive Rückkopplung (mit der Zeit) kriege, dann komme ich auf so eine Folge:

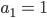
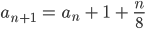
Die 8 hat er gewählt, weil er am 8. Geburtstag hat. Die Folge wächst prima. Ist aber eine rekursive Folge und schlecht zu berechnen, immer eins nach dem anderen. Im nächsten Spiel muss er

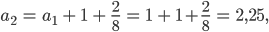
also 2 Tore werfen, dann

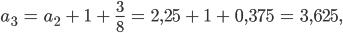
also 3 Tore usw. Das ist ja eine ewige Rechnerei!

Stetiges Modell anstelle der rekursiven Folge

Geht das besser mit Funktionen? Aber wie? Die Änderung von einem Spiel zum nächsten wäre

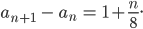
Jetzt hat er aber eine stetige Funktion f von der Zeit t, und die Differenz a_n+1 - a_n wird jetzt zum Differenzenquotienten

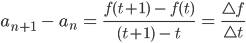
und den nähert er durch den Differenzialquotienten:

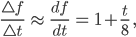
der Anfangswert bleibt natürlich:

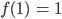
Die Ableitung df/dt kann Max gut integrieren:

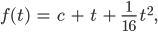
mit einer Konstanten c, das hatte er beim Abi. Wenn der Anfangswert gelten soll, dann muss die Konstante c zu -1/16 werden,

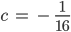
So er bekommt für das Modell mit der stetigen Funktion die Lösung:

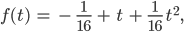
Fazit

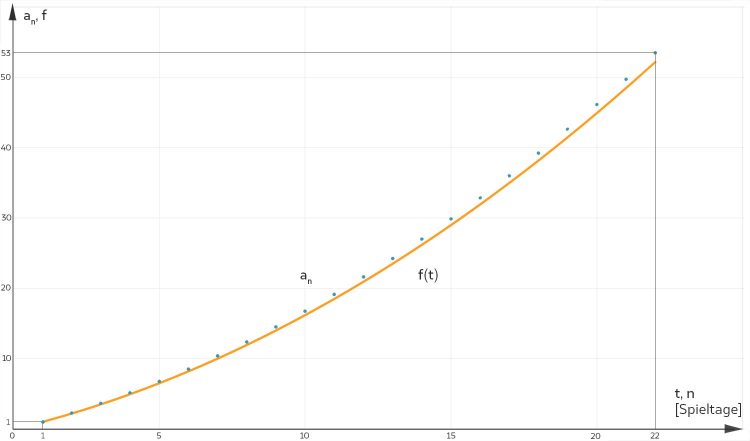
Max berechnet und zeichnet die Folge (a_n) und die Kurve f nun mit seinem Handy, wow, sie passen gut zusammen, er sieht nun, dass er beim letzten Spiel 53 Tore werfen muss. Das wäre der Rekord! Handball ist doch das Größte! Ja, der Matthäus-Effekt gilt beim Handball.

***

Übungsaufgaben

1. Was passiert, wenn die 8 durch eine beliebige Konstante ersetzt wird?
2. Was passiert für

Lösungen

1. Für

   erhält man:

2.