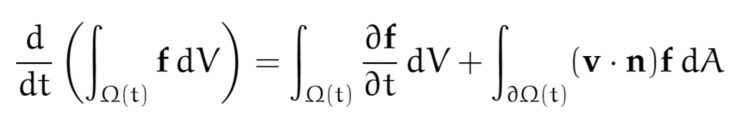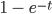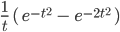Max hatte heute wieder Handballtraining. Außerdem hat es sich heute ergeben, dass er seine Abschlussarbeit in Indien machen wird. Er will für einen Sponsor eine Dokumentation über den Ausbau einer Internatsschule drehen. Bald muss er nach Indien fliegen. Doch heute Abend sind die beiden gemütlich bei Rike.
Max Hey Rike, heute war das Training echt anstrengend. Heute können wir nicht so schwierige Sachen besprechen.
Rike Klar, ich hatte heute auch nen langen Tag.
Max Sag mal Rike, was hast Du denn da fürn Bild hängen? Ist ja abgefahren!
Rike Das ist ein Bild von Ursula Ertz. Sie experimentiert gern mit Farben und arbeitet handwerklich. Sie lässt die Farben einfach übers Bild laufen.
Max Was?
Rike Schau mal hier, guck Dir mal den Ausschnitt an:
Konstellation für Transportgleichungen für viskose Flüssigkeiten
Da hast Du eine große gelbe Fläche, und Du siehst, wie das Gelb „weitergelaufen“ ist. Es ist eine wasserlösliche Farbe, die verläuft und mischt sich mit den anderen. Anfangs hatte sie vielleicht so ein Gebiet für Gelb:
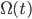ist der Bereich für Gelb, d.h. zur Zeit t, 
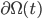sein Rand, 
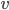ist die Fließrichtung der gelben Farbe, 
die Richtung der Normalen am Rand des GebietesDann floss die Farbe immer weiter und das Gebiet änderte sich mit der Zeit.
In diesem Gebiet 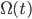finden Transporte statt, es werden Wasser und Farbpartikel transportiert – und nicht nur das, es findet auch eine Diffusion statt, die Farbe diffundiert in andere Farbflächen und in den Leinwanduntergrund. Je stärker die Konzentration der Partikel ist und je stärker ihr Gradient, umso stärker ist auch der Fluss.
Max Okay.
Rike Das ergibt die Navier-Stokes-Gleichungen. Die sind schon recht lange bekannt und warten noch auf ihre fundamentale Lösung. Dafür ist sogar ein Preis ausgeschrieben, 1 Million Dollar!
Max Hey, Rike, können wir das nicht irgendwie hinkriegen, kann doch gar nicht so schwer sein!
Rike Ach, das ist nicht unser Level. Außerdem haben wir hier viskose Flüssigkeiten, da wird alles noch viel komplizierter, dafür gibt es recht wenige Transportgleichungen – und die Aufgabe ist noch nicht als Wettbewerb ausgeschrieben. Aber ich habe eine schöne Eigenschaft für die gelbe Farbe gefunden.
Max Sags, ich sage Dir, ob es was taugt.
Reynolds-Integralgleichung
Rike Wenn
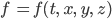
die Konzentration der gelben Partikel zur Zeit t am Ort (x, y, z) ist, dann gilt die Reynolds-Integralgleichung:
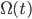... das zeitlich veränderliche Integrationsgebiet
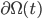... sein zeitlich veränderlicher Rand
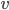... die Fließrichtung der gelben Farbe
... die Richtung der Normalen am Rand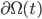 
des Gebietes 
,
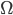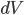... das Volumenelement für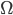
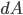... das Flächenelement für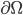 
Max Hmm.
Rike Das bedeutet, dass die zeitliche Änderung aller gelben Partikel im Gebiet 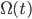genauso groß wie die Summe aller Gradienten von f und dem, was aus dem Gebiet rausfließt.
Max Okay, okay, ist doch klar.
Rike Ja, finde ich auch, ist ein schöner Satz für die Erhaltung aller Teilchen.
***
Übungsaufgaben
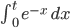
- Berechne
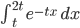
für
.
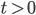