Rike hat von Freeman Dysons Tod gehört, hat seine Biografie Maker of Patterns gelesen und hat sich vorgenommen, eine seiner zahlentheoretischen Entdeckungen numerisch zu verifizieren. Doch sie kommt nicht weiter und fragt Ben.
Die ramanujansches Entdeckung
Rike Dysons Entdeckung geht so: Für jede Zahl der Gestalt
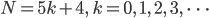
ist die Anzahl p ihrer Zerlegungen (partitions) in Summen (ohne Beachtung der Reihenfolge)
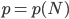
durch 5 teilbar. Außerdem ist für jede Zahl
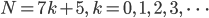
p(N) durch 7 teilbar und für
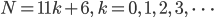
ist p(N) durch 11 teilbar. Das hat eigentlich schon Ramanujan herausgefunden.
Ben Okay, ich hab‘ da noch kein Gefühl dafür.
Rike Die Zahl 5, 7 bzw. 11 bezeichne ich mal mit q, dann ist die ramanujansche Entdeckung:
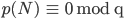
Lass uns das kleinste Beispiel nehmen,
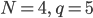
Die Zahl 4 lässt sich in 5 verschiedene Summen zerlegen:
| Nr. | Zerlegung |
| 1 | 4 |
| 2 | 3 + 1 |
| 3 | 2 + 2 |
| 4 | 2 + 1 + 1 |
| 5 | 1 + 1 + 1 + 1 |
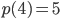
Ben Verstehe, das Schwierigste wird sein, systematisch die Zerlegungen zu finden, wie auf dem Rollfeld ...
Die dysonsche Entdeckung
Rike Haha, aber jetzt erst mal weiter. Dyson hat ein Kriterium gefunden, diese p(N) Zerlegungen in gleichgroße Klassen zu teilen.
Ben Aha! Bei 5 verschiedenen Zerlegungen kriege ich auch 5 verschiedene Klassen zu je 1 heraus, ich zähle einfach von 1 bis 5, basta!
Rike Ja. gut, bei 5 Klassen ist das trivial. Doch Dyson hat Klassen nach einem Merkmal der Zerlegung selbst – dem Rang – gefunden.
Ben Aha! Ein Ordnungskriterium! Und das willst du für große Zahlen testen?
Rike Richtig! Dysons Kriterium geht so: Zu jeder Zerlegung bestimmt er die Anzahl s der Summanden und außerdem den größten, largest Summanden l, und schließlich ist der dysonsche Rang m einer Zerlegung:
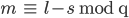
Ben Restklassen modulo q?
Rike Ja, genau.
"Kleines" Beispiel zum dysonschen Rang
Ben Dann, lass mal schauen:
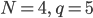
| Nr. | Zerlegung | s | l | l - s | m |
| 1 | 4 | 1 | 4 | 3 | 3 |
| 2 | 3 + 1 | 2 | 3 | 1 | 1 |
| 3 | 2 + 2 | 2 | 2 | 0 | 0 |
| 4 | 2 + 1 + 1 | 3 | 2 | -1 | 4 |
| 5 | 1 + 1 + 1 + 1 | 4 | 1 | -3 | 2 |
Okay. Lass uns mal ein nichttriviales Beispiel nehmen!
"Größeres" Beispiel für den dysonschen Rang
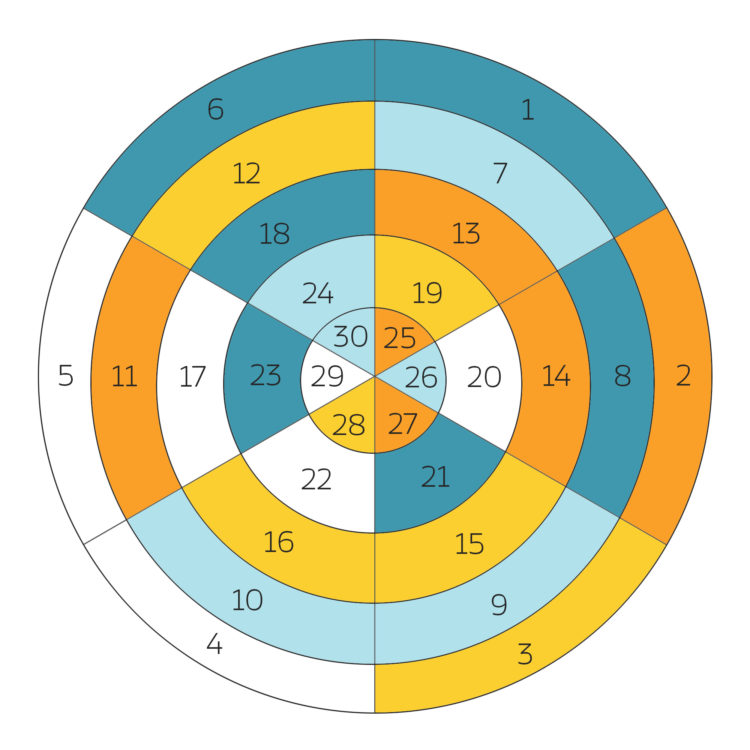
Rike Klar, für
kriege ich 30 Zerlegungen – von
bis
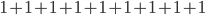
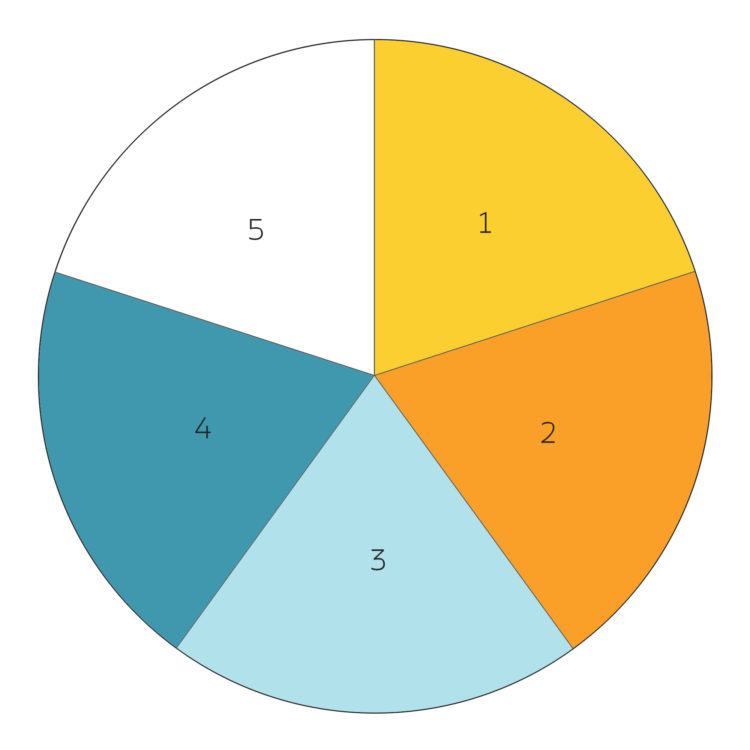
Die kann ich in 6 Klassen einteilen – je nach dem Rang m:
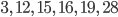
Nummern der Zerlegung mit m = 0
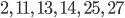
Nummern der Zerlegung mit m = 1
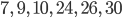
Nummern der Zerlegung mit m = 2
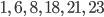
Nummern der Zerlegung mit m = 3
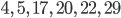
Nummern der Zerlegung mit m = 4
Ben Nicht schlecht! Da steckt eine höhere Ordnung drin? Hast du auch schon die anderen q’s probiert?
Rike Für kleinere Zahlen habe ich das gemacht, für größere will ich das programmieren. Doch Dyson schreibt selbst, er hat nur vermutet, dass sein Rang eine solche Klasseneinteilung zulässt für q = 5. Für q = 7 klappt das nicht immer und bei q = 11 funktioniert der Rang nicht. Hier schau mal:
Gegenbeispiel zum dysonschen Rang
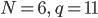
| Nr. | Zerlegung | s | l | l - s | m |
| 1 | 6 | 1 | 6 | 5 | 5 |
| 2 | 5 + 1 | 2 | 5 | 3 | 3 |
| 3 | 4 + 2 | 2 | 4 | 2 | 2 |
| 4 | 4 + 1 + 1 | 3 | 4 | 1 | 1 |
| 5 | 3 + 3 | 2 | 3 | 1 | 1 |
| 6 | 3 + 2 + 1 | 3 | 3 | 0 | 0 |
| 7 | 3 + 1 + 1 + 1 | 4 | 3 | -1 | 10 |
| 8 | 2 + 2 + 2 | 3 | 2 | -1 | 10 |
| 9 | 2 + 2 + 1 + 1 | 4 | 2 | -2 | 9 |
| 10 | 2 + 1 + 1 + 1 + 1 | 5 | 2 | -3 | 8 |
| 11 | 1 + 1 + 1 + 1 + 1 + 1 | 6 | 1 | -5 | 6 |
Ben Okay! Die 4. und 5. Zerlegung haben den selben Rang und die 7. und 8. Zerlegung ebenso. So kriegt er nur 9 Klassen statt 11. Und nun? Bist du die Erste, die das numerisch untersuchen will?
Der andrewssche und garvansche Crank
Rike Haha! Das wär’s! Ich, die Zahlentheoretikerin, die Ramanujan und Dyson fortsetzt! Doch Andrews und Garvan haben schon 1988 einen anderen Rang herausgefunden, einen Crank!
Ben Haha!
Rike Mit diesem Crank kann man die Zerlegungen auch für q = 7 und q = 11 in gleichgroße Klassen einteilen.
Ben Ist der Crank berechenbar?
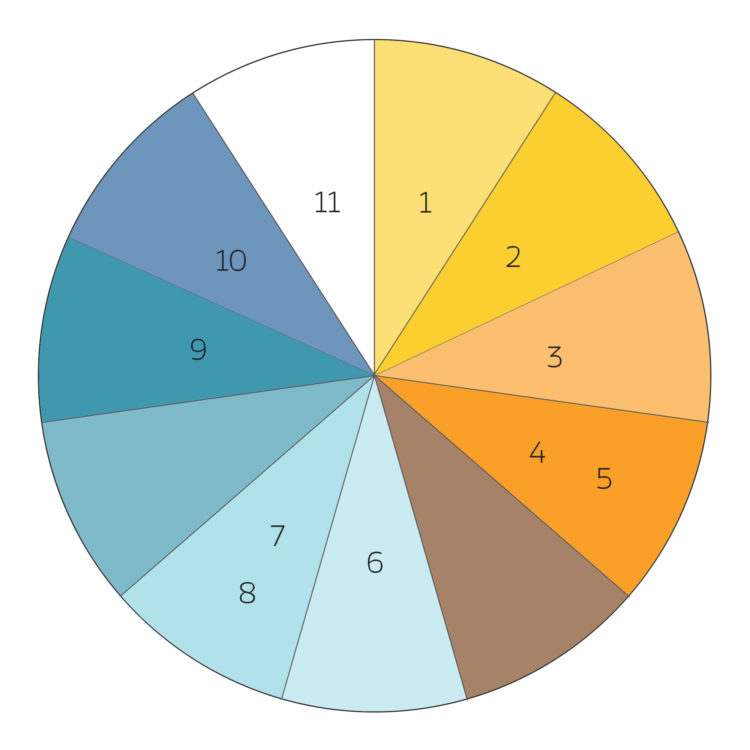
Rike Ja, klar: Wenn l der größte Summand einer Zerlegung ist, und l2 der 2. größte, dann soll
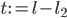
sein. lt+1 soll der t+1-größte Summand sein, wenn es den überhaupt gibt, sonst wird er zu Null gesetzt. Dann geht es weiter mit der Definition von d':
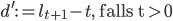
Der Crank d ist dann
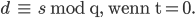
Beispiel zum andrewsschen and garvanschen Crank
Ben Okay, bei dem letzten 11er Beispiel kriegen wir
| Nr. | Zerlegung | s | t | d' | d |
| 1 | 6 | 1 | 6 | -6 | 5 |
| 2 | 5 + 1 | 2 | 4 | -4 | 7 |
| 3 | 4 + 2 | 2 | 2 | -2 | 9 |
| 4 | 4 + 1 + 1 | 3 | 3 | -3 | 8 |
| 5 | 3 + 3 | 2 | 0 | 2 | |
| 6 | 3 + 2 + 1 | 3 | 1 | 1 | 1 |
| 7 | 3 + 1 + 1 + 1 | 4 | 2 | -1 | 10 |
| 8 | 2 + 2 + 2 | 3 | 0 | 3 | |
| 9 | 2 + 2 + 1 + 1 | 4 | 0 | 4 | |
| 10 | 2 + 1 + 1 + 1 + 1 | 5 | 1 | 0 | 0 |
| 11 | 1 + 1 + 1 + 1 + 1 + 1 | 6 | 0 | 6 |
Rike Stimmt!
Ben Schön, da haben wir 11 verschiedene Klassen mit je einem Mitglied! Aber mit der Ordnungsstruktur sind wir noch nicht weitergekommen. Hast du mal ein Beispiel mit dem dysonschen Rang und dem Crank errechnet?
Rike Warte, ja, hier. das Beispiel mit N=9 und q = 5 haben wir mit dem dysonschen Rang berechnet. Die 30 Zerlegungen haben wir, für den Crank kriege ich andere Klassen. Grafisch sieht das so aus:
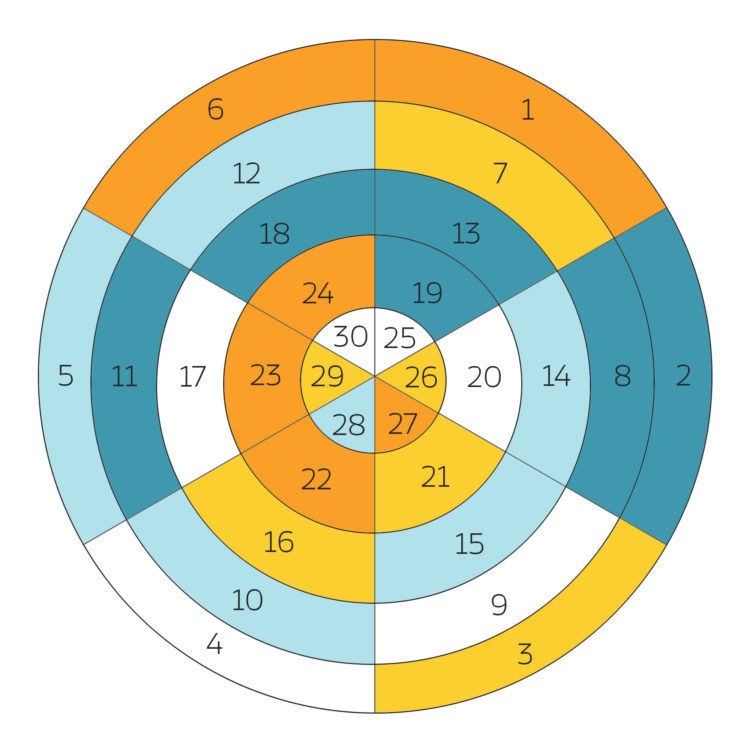
Ben Krass!
***
Übungsaufgabe
Überprüfe die Beispiele!
