Skip to main content


Zutaten: Zucker, Kakaomasse (50%), Milchzucker, Weizenmehl, Vollmilchpulver, Magermilchpulver, Butterreinfett, Sahnepulver, Butter (1,4%)
Kann Spuren von Analysis und Geometrie enthalten.

2020_23_dyson_partition-titel

Ein Algorithmus für Zerlegungen

Marietta Ehret Algebra, Numerik

Rike und Ben wollen ein Programm für die Zerlegungen von Zahlen in Summen entwerfen. Außerdem wollen sie für die speziellen Zahlen der Gestalt

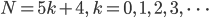
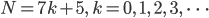
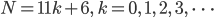
den dysonschen Rang m für jede Zerlegung und den andrewsschen & garvanschen Crank berechnen.

Dysons größtes Beispiel

Rike Dyson hat in seinem Buch Maker of Pattern erwähnt, dass er 1944 alles „mit Hand“ ausgerechnet hat. Er wollte seine Vermutung überprüfen, dass man mit dem Rang m alle Zerlegungen einer Zahl in gleich große Klassen einteilen kann. Er hat bei seinen Beispielen festgestellt, dass die Verteilung der Nummern in Klassen eher zufällig und gleichmäßig verläuft. Sein größtes Beispiel war

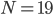
Dyson hat 490 Zerlegungen aufgeschrieben, wie lange er wohl dafür gebraucht hat?

Ben Lass uns ein paar Zerlegungen aufschreiben, was meinst du, wie könnte so ein Zerlegungs-Algorithmus aussehen?

Rike Ich würde den gern mal in Python programmieren, ich will da mal ein paar Erfahrungen machen.

Ben Naja, die tun sich mit Arrays schwer, aber wenn du es unbedingt kennenlernen willst…

Arrays und Sortierung von Zerlegungen

Rike Macht nichts! Python wirkt so modern, ich probier’s. Zerlegen kann man jede Zahl, ich habe ein paar Beispiele gerechnet und glaube, dass wir  einen Algorithmus finden können. Lass uns zur Diskussion eine kleine, aber nicht zu kleine Zahl nehmen, vielleicht

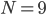
Das Beispiel habe ich ja schon gerechnet. Da haben wir 30 Zerlegungen, die schreibe ich dir gleich mal als Arrays.

Ben Liste heißt das.

Rike Okay, als Listen:

  1. [9]
  2. [8, 1]
  3. [7, 2]
  4. [7, 1, 1]
  5. [6, 3]
  6. [6, 2, 1]
  7. [6, 1, 1, 1]
  8. [5, 4]
  9. [5, 3, 1]
  10. [5, 2, 2]
  11. [5, 2, 1, 1]
  12. [5, 1, 1, 1, 1]
  13. [4, 4, 1]
  14. [4, 3, 2]
  15. [4, 3, 1, 1]
  16. [4, 2, 2, 1]
  17. [4, 2, 1, 1, 1]
  18. [4, 1, 1, 1, 1, 1]
  19. [3, 3, 3]
  20. [3, 3, 2, 1]
  21. [3, 3, 1, 1, 1]
  22. [3, 2, 2, 2]
  23. [3, 2, 2, 1, 1]
  24. [3, 2, 1, 1, 1, 1]
  25. [3, 1, 1, 1, 1, 1, 1]
  26. [2, 2, 2, 2, 1]
  27. [2, 2, 2, 1, 1, 1]
  28. [2, 2, 1, 1, 1, 1, 1]
  29. [2, 1, 1, 1, 1, 1, 1, 1]
  30. [1, 1, 1, 1, 1, 1, 1, 1, 1]

Ben Aha! Wie bist du vorgegangen?

Rike Meine Sortierung der Zerlegungen ist so, dass in jeder Zerlegung die größten Summanden links stehen und danach werden sie immer kleiner. Außerdem steht die Zerlegung mit dem größten ersten Summanden vor der Zerlegung mit dem nächstkleineren ersten Summanden.

Ben Ach ja, die lexikografische Ordnung!

Rike Ja. Meine wichtigste Idee ist, aus einer Zerlegung die nächste zu finden, indem ich die Summanden immer kleiner mache. So lange, bis alle Summanden zu 1 geworden sind. Die Null zählt natürlich nicht mit.

Ben Gut, das können wir für den Algorithmus übernehmen.

Eine wiederverwendbare Liste partition

Rike Dann starten wir mit

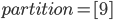
Ben Gut. Weil es aber in Python so umständlich ist, dynamisch immer neue Listen zu kreieren und zu bezeichnen, würde ich die Liste partition ausgeben und dann mit der nächsten überschreiben. Weil du aber die alte zur Berechnung der neuen brauchst, machst du eine Kopie von der Liste partition, sagen wir mal partition1. Außerdem legst du die neue Liste partition leer an, das geht so:

23_kopieren_02

Zu jeder Partition rechnest du den Rang m aus und was du sonst noch so brauchst. Ist das viel?

Rike Zu jeder Zerlegung brauche ich den größten Summanden l, die Anzahl der Summanden s und den Rang m :

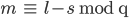
Den Index jeder Zerlegung (num_p) muss ich dann je nach Rang m in eine der Restklassen modulo q speichern.

Ben Okay. Das kannst du zu jeder Zerlegung ausrechnen.

Divison modulo q

Rike Klar, mache ich. Kann den Python auch die Division mit den Restklassen?

Ben Aaah, manchmal klappt das nicht, weil die Datentypen frei sind, aber das ist schnell programmiert. Wenn eine Zahl größer als q ist, ziehst du immer wieder q ab, bis das Ergebnis zwischen 0 und q - 1 liegt; wenn deine Zahl kleiner als Null ist, addierst du eben immer wieder q. Das machst du [m/q] mal, so sieht das aus:

23_rang_02

Zerlegungen

Rike Verstehe! Jetzt die Zerlegungen – das Schwierigste!

Ben Wie bist du konkret vorgegangen?

Fall [9]

Rike Der einfachste Fall kommt gleich am Anfang. Aus

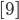
mach‘ ich

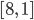
Ben Okay, das kannst du immer machen, wenn die letzte Zahl keine 1 ist. Du subtrahierst vorne 1 und fügst hinten eine 1 an.

Fall [6, 2, 1]

Rike Richtig. Jetzt kommen all die Fälle, wo hinten schon Einsen stehen. Das wird schwieriger. Aber immer, wenn eine Zwei vor den Einsen steht, kann ich sie in zwei Einsen zerlegen.

Ben Klar, aus [6, 2, 1] wird [6, 1, 1, 1], du musst die Zwei durch eine Eins ersetzen und eine Eins anfügen.

Fälle [8, 1] vs. [5, 1, 1, 1, 1]

Rike Okay. Weiter, für die Zerlegung nach [8, 1] ziehe ich wieder 1 von der 8 ab und addiere den Rest - eben

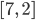
Ich habe schon mal versucht, das zu automatisieren, aber bei der Zerlegung nach

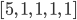
käme ich dann auf

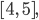
wenn ich das genauso mach wie bei [8, 1]. Das ist leider nicht richtig sortiert und [5, 4] war schon dran!

Ben So einen Fall kannst du doch feststellen. Du brauchst zuerst die Anzahl der Einsen in der Liste, die nennen wir mal x. Du fragst danach, ob

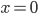
ist. Wenn ja, dann hast du den Fall [9]. Aus dem machst du [8, 1].

Rike Klar!

Ben Weiter. Wenn

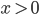
wird es etwas schwieriger. Aus [8, 1] wollen wir [7, 2] machen, und das ist okay, weil x=1 und die neue Zahl vor der Eins 7 ist. Bei

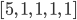
ist

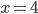
und die neue Zahl vor der 1 ist jetzt 4. Das müssen wir in ein Kriterium wandeln. Hmm.

Rike Hmm, wenn die neue Zahl vor der Eins ‘mal zahl_vor_der_1 nennen, dann ist

zahl_vor_der_1

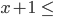
bei [8, 1] erfüllt und bei [5, 1, 1, 1, 1] nicht.

Anzahl x bzw. s der Einsen bzw. Summanden

Ben Gut, dann haben wir – glaube ich – Alles. Jetzt müssen wir das nur noch allgemeiner aufschreiben, nicht an das Beispiel gebunden. Du berechnest die Anzahl x der Einsen und außerdem brauchst du ja auch für deinen Rang die Anzahl s der Summanden:

23_x_und_s_bestimmen_02

Rike Okay.

Programm für beliebige N

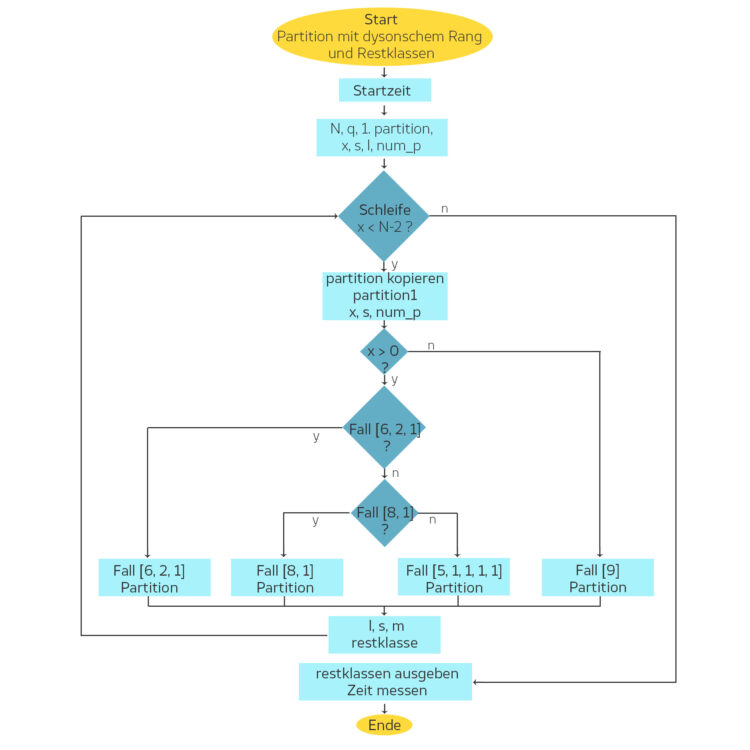
23_flowchart_03
Flowchart für Rikes und Bens Algorithmus

Ben Wir notieren einfach die einzelnen Schemata:

Fall [9] verallgemeinert

Kriterium

23_tabellen_05_fall_9_02

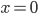
Fall [6, 2, 1] verallgemeinert

Kriterien

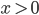
Zahl vor den Einsen: 2

23_tabellen_05_fall_6_2_1_02

Fall [8, 1] verallgemeinert

Kriterien

zahl_vor_der_1

23_tabellen_05_fall_8_1_03

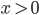
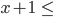
Fall [5, 1, 1, 1, 1] verallgemeinert

Kriterien

zahl_vor_der_1

23_tabellen_05_fall_5_1_1_1

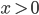
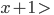
Rike Alles klar! Dann implementiere ich das mal! Und dann setze ich N = 19, q = 5 ein. Mal sehen, ob ich auch 490 Zerlegungen bekomme und wie lange das dauert!

Ben Viel Spaß!

***

Übungsaufgaben

Programmiere selbst einen Algorothmus für Zerlegungen. Teste N = 19, q = 5. Welche Zeit braucht dein PC?

Lösungen

23_programm_N_19_q_5_01
Anfang des Programms
23_loesung_N_19_q_5_01_01
Ausgabe der Zerlegungen für N = 19, q = 5, Teil 1
23_loesung_N_19_q_5_01_02
Ausgabe der Zerlegungen für N = 19, q = 5, Teil 2
23_loesung_N_19_q_5_01_03
Ausgabe der Zerlegungen für N = 19, q = 5, Teil 3

 

23_loesung_N_19_q_5_01_04
Ausgabe der Zerlegungen für N = 19, q = 5, Teil 4
23_loesung_N_19_q_5_01_05
Ausgabe der Zerlegungen für N = 19, q = 5, Teil 5

 

3_loesung_N_19_q_5_01_06
Ausgabe der Zerlegungen für N = 19, q = 5, Teil 6
23_loesung_N_19_q_5_01_07
Ausgabe der Zerlegungen für N = 19, q = 5, Teil 7
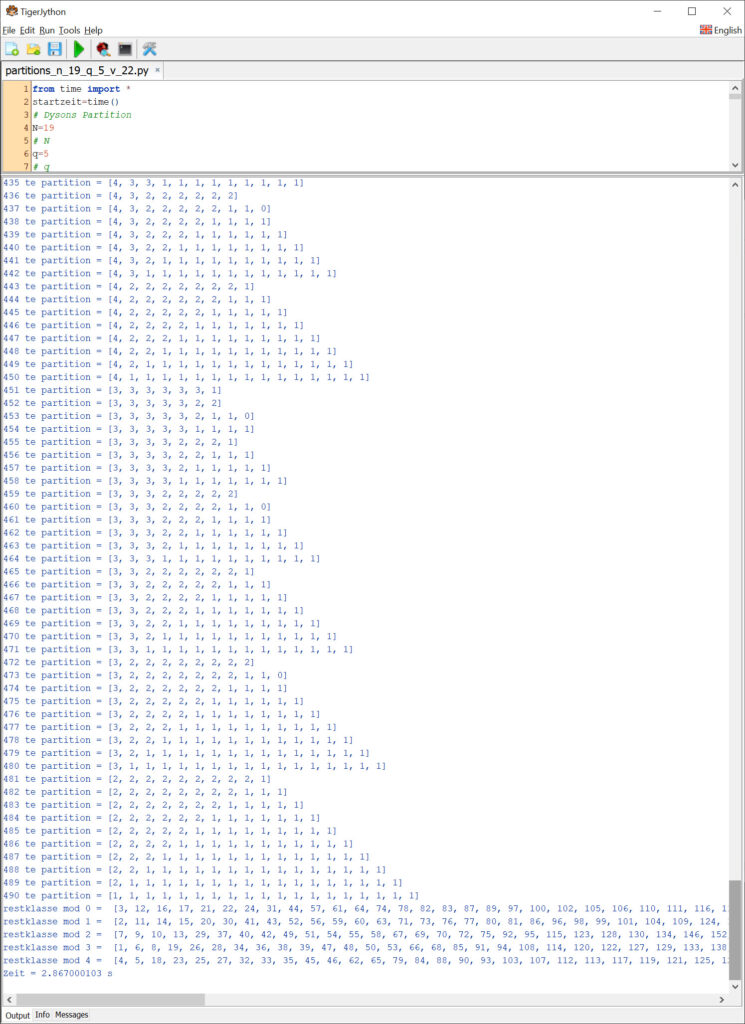
23_loesung_N_19_q_5_01_08
Ausgabe der Zerlegungen für N = 19, q = 5, letzter Teil

Rike braucht ca. 3 s für Berechnung und Ausgabe an ihrem Notebook.