Clusterbildung in Restklassen

Ben und Rike haben ein Programm zur Bestimmung von Zerlegungen von Zahlen N als Summen erstellt. Diese Zerlegungen wurden indiziert – von 1 bis num_p. Zu jeder Zerlegung haben sie den dysonschen Rang m modulo q berechnet. Für bestimmte Zahlen N erhält man dann gleichgroße Restklassen von Zerlegungen. Doch wie sind die Indizes verteilt? Sind sie gleichverteilt und sehr zufällig, wie Dyson vermutete oder bilden sich Cluster?

Zerlegungen und Restklassen für N = 9, q = 5

Zunächst betrachten sie wieder N = 9, q = 5. Doch diesmal nehmen sie nicht den dysonschen Rang m sondern den universelleren Crank d von Andrews & Garvan. Sie erhalten die Zerlegungen

[9]
[8, 1]
[7, 2]
[7, 1, 1]
[6, 3, 0, 0]
[6, 2, 1, 0]
[6, 1, 1, 1]
[5, 4]
[5, 3, 1]
[5, 2, 2]
[5, 2, 1, 1]
[5, 1, 1, 1, 1]
[4, 4, 1]
[4, 3, 2]
[4, 3, 1, 1]
[4, 2, 2, 1]
[4, 2, 1, 1, 1]
[4, 1, 1, 1, 1, 1]
[3, 3, 3]
[3, 3, 2, 1]
[3, 3, 1, 1, 1]
[3, 2, 2, 2]
[3, 2, 2, 1, 1]
[3, 2, 1, 1, 1, 1]
[3, 1, 1, 1, 1, 1, 1]
[2, 2, 2, 2, 1]
[2, 2, 2, 1, 1, 1]
[2, 2, 1, 1, 1, 1, 1]
[2, 1, 1, 1, 1, 1, 1, 1]
[1, 1, 1, 1, 1, 1, 1, 1, 1]

Die kann Rike in 6 Klassen einteilen – je nach dem Crank d:

Indizes der Zerlegung mit d = 0

Indizes der Zerlegung mit d = 1

Indizes der Zerlegung mit d = 2

Indizes der Zerlegung mit d = 3

Indizes der Zerlegung mit d = 4

Clusterbildung im Kreis

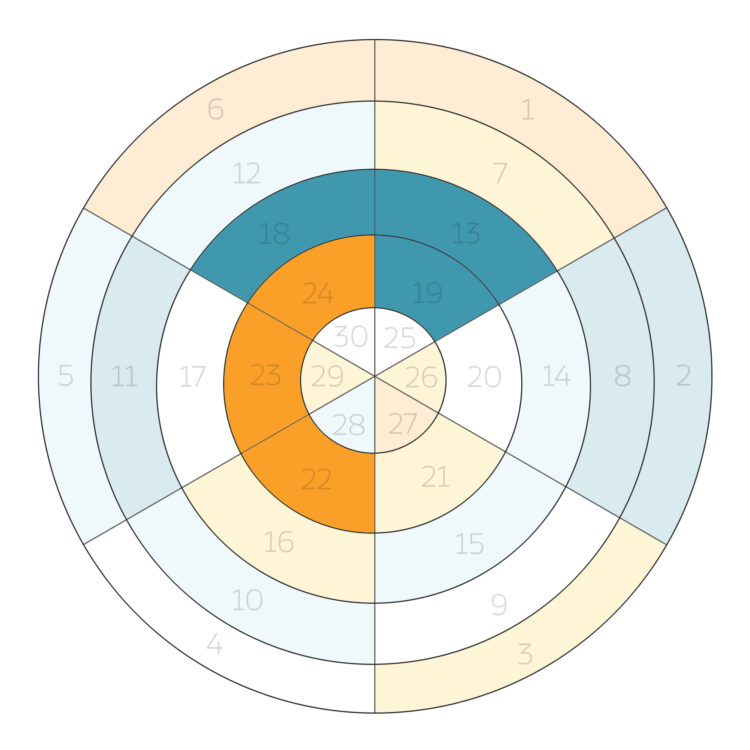
24-restklassen_andrews_6_04 — Clusterbildung in Restklassen (Kästchen derselben Farbe)

Dabei stellt Rike fest, dass einige – wie die 22, 23, 24 – in derselben Restklasse liegen und Cluster bilden und andere nicht. Doch wie soll man das ausrechnen? Da fragt sie Ben.

Clusterbildung im rechteckigen Gitter

Ben Wenn ich das richtig verstanden habe, geht es hier um Gitter modulo q. Dann solltest du besser Rechtecke zeichnen und die Rechtecke periodisch fortsetzen:

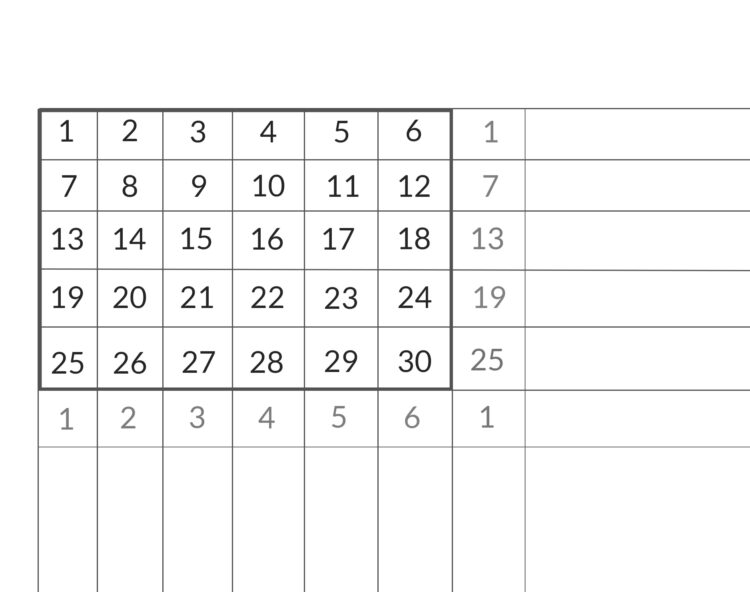
24-restklassen_andrews_7_02 — Darstellung von 30 Zerlegungen im rechteckigen wiederholten Gitter

Wenn du hier die linke und rechte Seite zusammenführst und alles ein bisschen verbiegst, kommst du auch auf deinen Kreis.

Rike Sehr witzig!

Ben Ja! Und hier setzen wir die untere Kante mit der oberen fort. Das ist ein schönes Modell für Gitterstrukturen, und vielleicht bietet dieser Crank eine Beschreibung von neuen Geometrien in neuen Materialien?

Rike Das hoffe ich!

Cluster I

Ben Zuerst würde ich die einfachsten Cluster suchen, nämlich Paare. Das allereinfachste Cluster läge dann horizontal innerhalb des originalen Rechtecks:

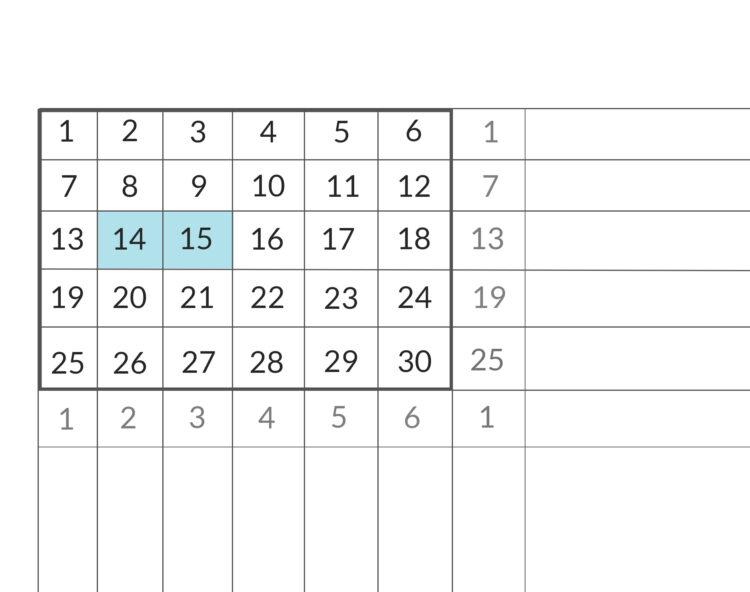
24-restklassen_andrews_7_cluster_1_02 — Cluster vom Typ I – horizontal, innen

Jetzt müssen wir nur ein Kriterium finden, um solche Zahlen aus einer Restklasse herauszufiltern. Na?

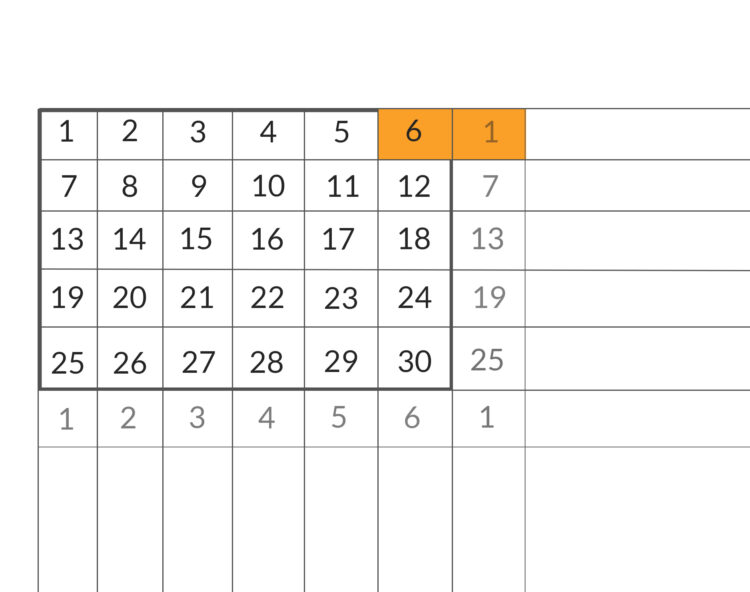
Rike Na, ist doch einfach, wenn 2 Zahlen z_i und z_j in einer Restklasse liegen, dann müsste

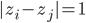
sein.

Ben Okay. Aber wie testet du, dass die beiden Zahlen horizontal im Innern liegen?

Rike Hmm …. Also [18, 19] dürften allein kein Cluster bilden, obwohl ihre Differenz 1 ist? Dann sollte die größere der beiden Zahlen nicht am rechten Rand stehen oder die kleiner der beiden nicht am linken. Am rechten Rand sind die Zahlen durch 6 teilbar, am linken lassen sie den Rest 1.

Cluster II

Ben Super! Weiter. Wenn zwei benachbarte Zahlen übereinander liegen, was dann?

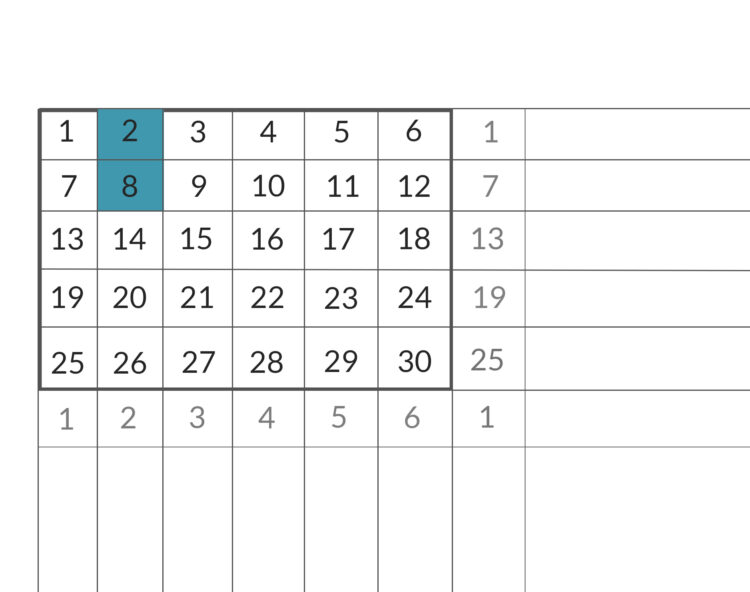
24-restklassen_andrews_7_cluster_2_02 — Cluster vom Typ II – vertikal, innen

Rike Dann hätten wir

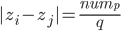
Bei diesem Bespiel ist

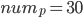
und

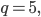
also

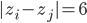
Ben Richtig. Am seitlichen Rand wird es etwas schwieriger:

Cluster III

24-restklassen_andrews_7_cluster_3_02 — Cluster vom Typ III – am linken oder rechten Rand

Rike Okay, da muss ich prüfen, ob die beiden Zahlen z_i und z_j in einer Reihe liegen. Die Zahlen der letzten Spalte sind gerade durch 6 teilbar, das hatten wir eben schon, also Vielfache von

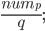
das ergibt

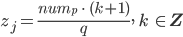
Der Index z_i in der ersten Spalte ist von der Form

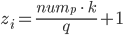
mit demselben ganzen k.

Cluster IV

Ben Hey, Rike, nicht schlecht! Bei N = 9 haben wir zwar kein vertikales Paar, aber wie könnte das Kriterium heißen, wenn wir eins hätten?

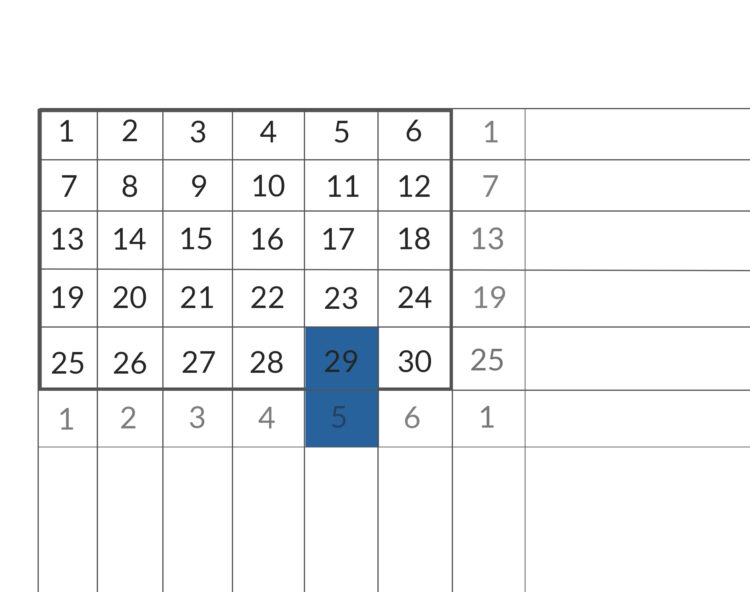
24-restklassen_andrews_7_cluster_4_02 — Cluster vom Typ IV – am unteren oder oberen Rand

Rike Hmm… Bei uns im Beispiel wäre die Differenz zweier übereinanderliegenden Zahlen immer 24, das ist 6 – die Anzahl der Elemente in den Restklassen – multipliziert mit 4 – das ist q - 1, also

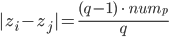
Ben Okay, größere Cluster kannst du dir selbst überlegen, das ist recht ähnlich.

Rike Hmm.

Mittelwerte in den Restklassen

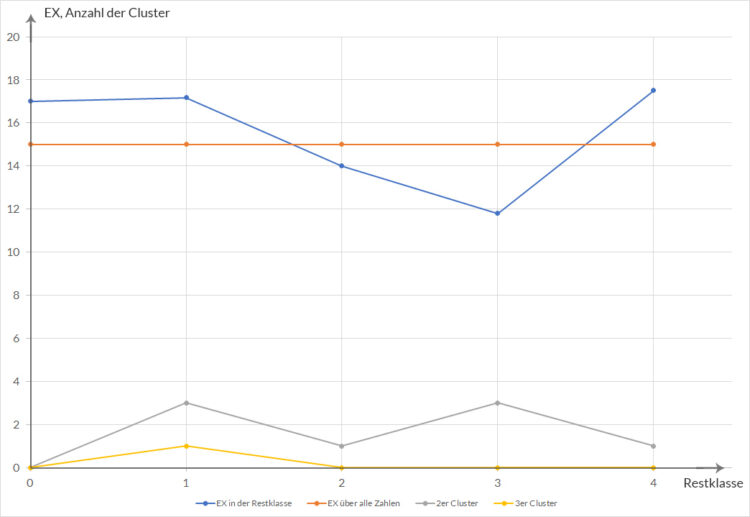
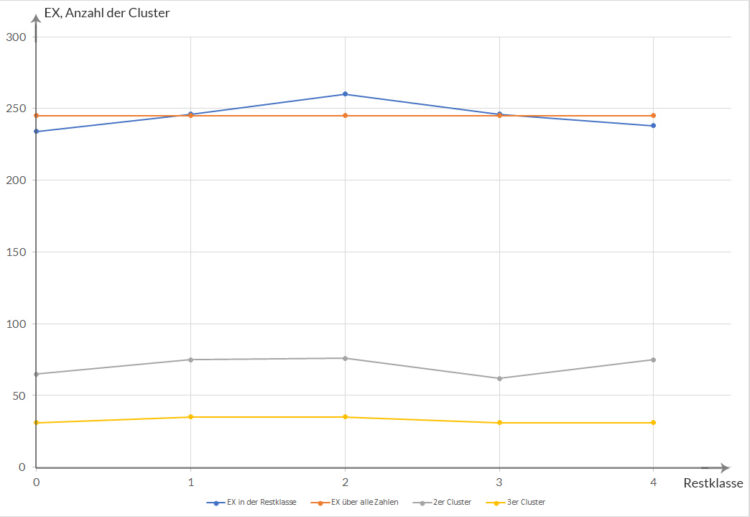
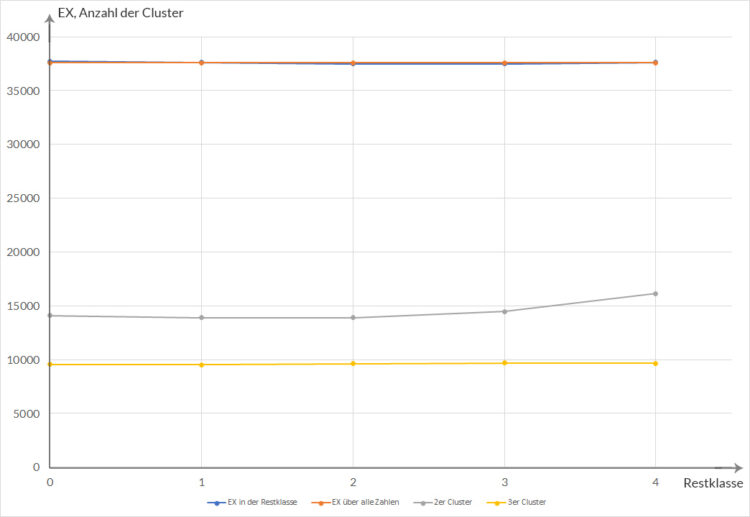
Ben Dann kannst du anfangen mit dem Implementieren. Meiner Meinung nach könnte Gleichverteilung auch heißen, dass die Zahlen gleichverteilt sind, kannst du nicht gleich noch den Mittelwert in jeder Restklasse ausrechnen und mit dem Mittelwert über alle Zahlen vergleichen?

Rike Okay, das schaffe ich auch noch!

***

Übungsaufgabe

Zähle die beschriebenen Cluster und bestimme Mittelwerte für einige N.