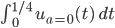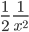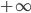Lila erzählt Max von ihrem Mathestudium an einer Berliner Uni. Sie war sehr wütend über den Rausschmiss von Kubicki und hatte sich erst einmal zurückgezogen. Von Zeit zu Zeit ging sie in die Unibibliothek. So einen Wissensschatz hat sie in Indien noch nie gesehen. Es gefällt ihr dort. Sie wundert sich, dass so wenige ihrer Kommilitonen dort lernen. Sie hat ein bemerkenswertes Buch entdeckt.
Lila Dieses CRC Handbook of Mathematical Curves and Surfaces ist von von Seggern, von einem Geologen. Es ist von 1990. Da war die very first time of personal computer gerade vorbei, und die Zeiten guter grafischer Darstellung noch nicht angebrochen. Immerhin hat er mit der „High-level programming language“ FORTRAN(!) seine Kurven berechnet. Von Seggern ist Spezialist für Erdbeben und Analysen von unterirdischen Nukleartests. Er hat ca. 500 Kurven und Flächen gezeichnet, einfach, um einen grafischen Überblick zu bekommen und seiner Firma zur Verfügung zu stellen. Die meisten Kurven sind parameterabhängig.
Max Krass! Ein Katastophenspezialist! Wie läuft denn bei ihm die Zeit – vorwärts oder rückwärts?
Lila Haha, ganz klassisch vorwärts!
Tsunamiwellenkurven
Eine seiner Kurven ist
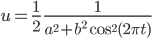
Diese Funktion hat 2 Parameter, a und b. Eigentlich kommt es nur auf das Verhältnis von beiden an, b setzen wir mal 1:
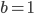
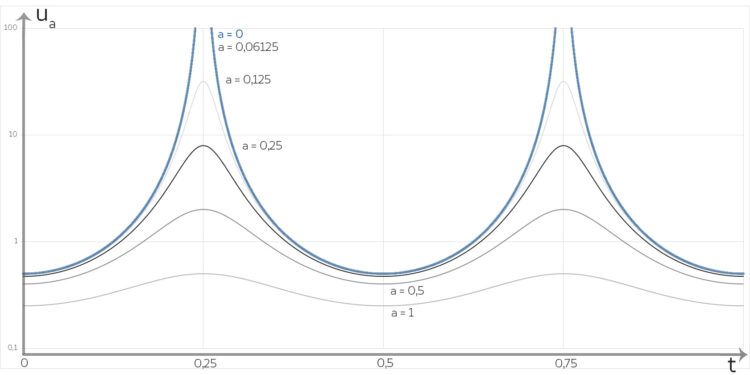
Für a nimmt er die Werte
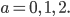
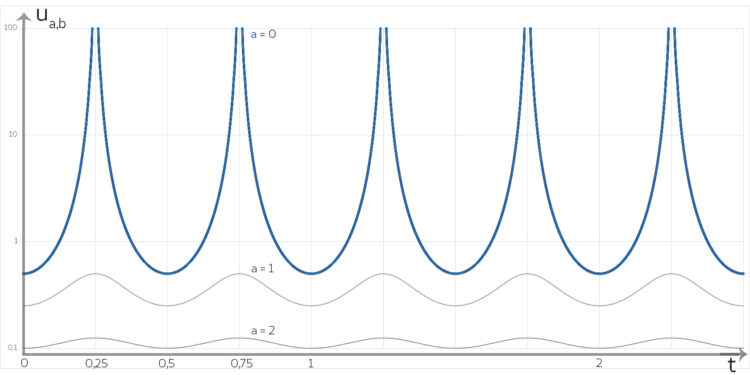
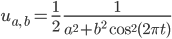für verschiedene Parameter a und b=1.Max Nicht schlecht!
Polstellen
Lila Du verstehst, es hat mir sofort gefallen. Dieser Übergang von sanften Wellen zu gigantischen Tsunamiwellen, einfach, wenn man a kleiner werden lässt, is marvellous. Doch man kann es schnell erklären und braucht nicht mal eine high-level programming language dazu. Der Nenner kann Null werden:
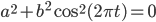
You see, wenn wir das umstellen, dann wird der Nenner Null, genau dann, wenn
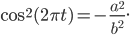
Weil die linke Seite der Gleichung immer nicht negativ ist und die rechte Seite immer nicht positiv, kann die Gleichung nur für a = 0 erfüllt werden. Die Zeiten t = tk, wo das gilt, berechnet man aus den Nullstellen des Kosinus:
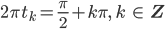
also
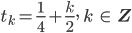
Du siehst, dass es unendlich viele tk gibt. Also hat die Ausgangsfunktion
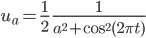
an den Stellen t = tk Polstellen – aber nur für a = 0 .
Max Okay, verstehe.
Lila Mich hat besonders interessiert, wie dieser Übergang von braven Wellen zu Tsunamiwellen mit
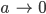
vor sich geht. Wenn ich näher herangehe, sieht das so aus:
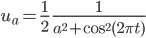für verschiedene Parametern a nahe 0.
Differenzfunktion
Für a = 0,06125 kann ich die Kurve grafisch nicht mehr von der für a = 0 unterscheiden.
Max So geht mir das auch immer...
Lila So blieb mir nichts übrig, als die Differenz der beiden Funktionen
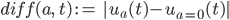
zu berechnen.
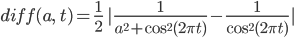
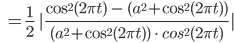
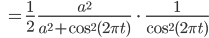
Max Mannometer!
Lila Lass uns nur den ersten Grenzwert an der ersten Polstelle
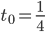
berechnen. Da geht
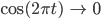
Lilas Substitution
Das können wir substituieren: Wir setzen
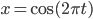
Dann geht x nach 0:
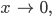
wenn t nach ¼ strebt:
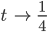
Max Irgendwie redest du jetzt schon wie eine richtige Mathematikerin.
Lila Haha. Also, verstehst du das?
Max Ja, schon gut.
Lila Dann wird aus meiner Differenzfunktion diff eine neue Funktion, ich lass den Namen mal, okay?
Max Okay.
Lila
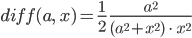
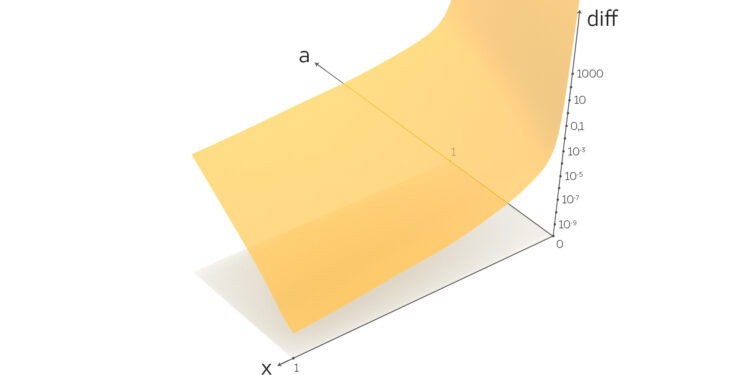
Fazit
Die kann ich gut grafisch darstellen. Da siehst du, dass die Differenzfunktion für
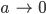
und
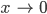
unendlich groß wird. Das heißt, in den Polstellen gibt es keinen stetigen Übergang von der einen Welle mit a > 0 zur anderen mit a = 0. Die Tsunamiwelle ist immer noch unendlich weit von der anderen Welle entfernt.
***
Übungsaufgaben
- Berechne den Grenzwert
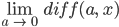
für x > 0, fest.
- Berechne den Grenzwert
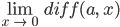
für a > 0, fest.
- Berechne
- Berechne den Grenzwert
