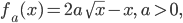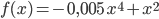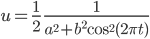Zutaten: Zucker, Kakaomasse (50%), Milchzucker, Weizenmehl, Vollmilchpulver,
Magermilchpulver, Butterreinfett, Sahnepulver, Butter (1,4%)
Kann Spuren von Analysis und Geometrie enthalten.

Rike hat schon gemerkt, dass ihre zufällige Anordnung von 6 Blumen pro Quadratmeter Charly in der IGA-Aufgabe nicht gefallen hat, ja, dass diese Lösung nicht nur Charly nicht gefällt sondern auch auf der IGA 2017 keinen Beifall gefunden hätte. So überlegt sie, ob es nicht doch eine seriöse Lösung gibt. Sie erinnert sich, dass Gärtner häufig diagonale Anordnungen benutzen. Eine Diagonale ergäbe so ein 5er Muster. Weiterlesen

Charly bereitet sich an einem Sonntagmorgen auf das nächste Schulhalbjahr vor und schaut sich die letzten Mathe-Abiaufgaben an. Die Analysis-Aufgabe zur Internationalen Gartenbauausstellung 2017 in Berlin hat es ihm besonders angetan.
In dieser Aufgabe soll ein rechteckiges Beet (16 m x 6 m) durch Kurven der Form
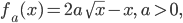
geteilt werden, siehe Abbildung.
Weiterlesen

Rike und Charly haben Sommerferien. Während Charly im Wald joggt, schaut sich Rike Charlys Sammlung ehemaliger Abi-Aufgaben an. Da findet sie diese Bonsai-Aufgabe:
Die originale Bonsai-Aufgabe
2.2 Analysis: Bonsai-Bäume
Bonsai bezeichnet eine spezielle japanische Gartenkunst, bei der Bäume durch Züchtung in einem Gefäß extra klein gehalten werden. Das Wachstum eines bestimmten Bonsai-Baumes lässt sich bis zum Erreichen der maximalen Höhe für t ≥ 0 mit der Funktion
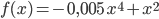
beschreiben.
Dabei gibt t die Zeit in Jahren und f(t) die Höhe in cm an.
a) Bestimmen Sie die Höhe des Baumes nach 4 Jahren und nach 8 Jahren.
b) Berechnen Sie die maximale Höhe des Baumes. Geben Sie an, wie viele Jahre der Baum wächst.
c) Berechnen Sie die höchste Wachstumsgeschwindigkeit. Es genügt die Bearbeitung mit dem notwendigen Kriterium.
[…]
[Mathematik Abitur 2022, S. 72 ]
Weiterlesen

Rike fährt zu ihrer Schwester Jule nach Aachen. Die hat ihr Informatikstudium erfolgreich abgeschlossen, hat sich für ein Masterstudium an der RWTH Aachen entschieden und ist nun schon das 1. Jahr dabei. Rike muss einfach mal raus aus Berlin. Sie ist schon lange zusammen mit Ben im Home Office. Sie testet verschiedene Software zur intelligenten und selbstlernenden Mustererkennung für eine spezielle Anwendung. Doch der Auftraggeber hat den Auftrag zurückgezogen und Rike wurde gekündigt. Sie ist ziemlich wütend darüber.
Weiterlesen

Max und Lila sind heute im Schnee unterwegs. Als sie einen Fuchs sehen, fällt Lila eine von den Krotofil-Vorlesungen ein. Ganz begeistert erzählt sie Max davon. Es geht um ein weiteres motivierendes Beispiel für Differenzialgleichungen: das Räuber-Beute-System nach Lotka-Volterra. Weiterlesen

Ben und Rike bleiben am Nord-Ostsee-Kanal. Jetzt wollen sie sowieso nicht nach Berlin zurück. Sie bewundern die turbulente Strömung im Nord-Ostsee-Kanal hinter einem Schiff. Weiterlesen

Rike und Ben sind immer noch am Nord-Ostsee-Kanal bei Brunsbüttel. Hinter jedem Schiff bilden sich Wellen. Diese genügen der Navier-Stokes-Gleichung – und die ist immer noch eine Herausforderung. Recht einfach sind gleichmäßige Wellen in einer Richtung zu verstehen. Sie bilden eine spezielle Lösung dieser Gleichung. Rike konstruiert auch noch einen passenden Hilbertraum dafür.
Weiterlesen

Lila erzählt Max von weiteren Funktionen des Geologen und Erdbeben- und Nukleartestforschers von Seggern.
Lila Die letzte Funktion
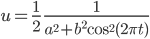
hat für a = 0 Polstellen. Wenn ich die Fläche von 0 bis zur 1. Polstelle berechne – die könnte ja für die Energie stehen, die bei einem solchen Erdbeben frei wird – so kommt leider unendlich raus. D.h. schon ein einziger Stoß von dieser Sorte setzt viel zu viel Energie frei. Ich find‘s jammerschade, dass die bis jetzt nicht konstruktiv genutzt werden kann, sondern nur destruktiv ist. Da wird mir beim Rechnen richtig unbehaglich. Weiterlesen

Lila erzählt Max von ihrem Mathestudium an einer Berliner Uni. Sie war sehr wütend über den Rausschmiss von Kubicki und hatte sich erst einmal zurückgezogen. Von Zeit zu Zeit ging sie in die Unibibliothek. So einen Wissensschatz hat sie in Indien noch nie gesehen. Es gefällt ihr dort. Sie wundert sich, dass so wenige ihrer Kommilitonen dort lernen. Sie hat ein bemerkenswertes Buch entdeckt.
Lila Dieses CRC Handbook of Mathematical Curves and Surfaces ist von von Seggern, von einem Geologen. Es ist von 1990. Da war die very first time of personal computer gerade vorbei, und die Zeiten guter grafischer Darstellung noch nicht angebrochen. Immerhin hat er mit der „High-level programming language“ FORTRAN(!) seine Kurven berechnet. Von Seggern ist Spezialist für Erdbeben und Analysen von unterirdischen Nukleartests. Er hat ca. 500 Kurven und Flächen gezeichnet, einfach, um einen grafischen Überblick zu bekommen und seiner Firma zur Verfügung zu stellen. Die meisten Kurven sind parameterabhängig.
Weiterlesen
 zwischen den Kurven
zwischen den Kurven 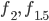 und der
und der  -Achse von knapp 30 m² ausgelegt.
-Achse von knapp 30 m² ausgelegt.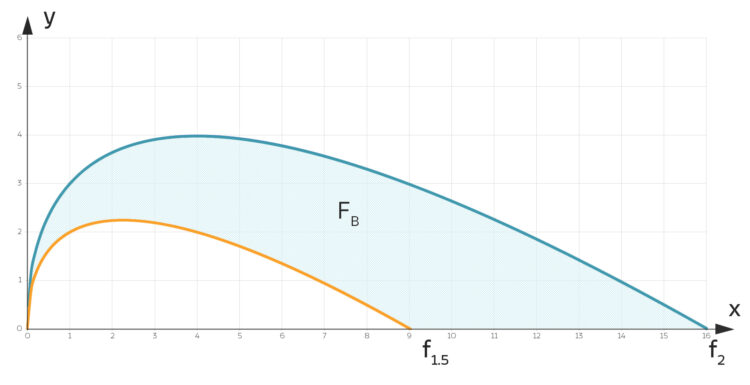
 , die mit Blumen zu belegen ist. Für die Formeln von
, die mit Blumen zu belegen ist. Für die Formeln von 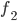 und
und 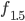 siehe Beitrag Die IGA-Aufgabe.
siehe Beitrag Die IGA-Aufgabe.