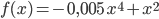Rike und Charly haben Sommerferien. Während Charly im Wald joggt, schaut sich Rike Charlys Sammlung ehemaliger Abi-Aufgaben an. Da findet sie diese Bonsai-Aufgabe:
Die originale Bonsai-Aufgabe
2.2 Analysis: Bonsai-Bäume
Bonsai bezeichnet eine spezielle japanische Gartenkunst, bei der Bäume durch Züchtung in einem Gefäß extra klein gehalten werden. Das Wachstum eines bestimmten Bonsai-Baumes lässt sich bis zum Erreichen der maximalen Höhe für t ≥ 0 mit der Funktion
beschreiben.
Dabei gibt t die Zeit in Jahren und f(t) die Höhe in cm an.
a) Bestimmen Sie die Höhe des Baumes nach 4 Jahren und nach 8 Jahren.
b) Berechnen Sie die maximale Höhe des Baumes. Geben Sie an, wie viele Jahre der Baum wächst.
c) Berechnen Sie die höchste Wachstumsgeschwindigkeit. Es genügt die Bearbeitung mit dem notwendigen Kriterium.
[…]
[Mathematik Abitur 2022, S. 72 ]
Rike regt sich ziemlich darüber auf. So viele Missverständnisse! x und t werden verwechselt, Wachstum wird mit Höhe gleichgesetzt, was ist dann "Wachstumsgeschwindigkeit"? Weshalb genügt die Bearbeitung mit dem notwendigen Kriterium?
Schnell hat sie die Kurve
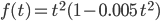
analysiert und gezeichnet, Nullstellen bei
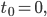
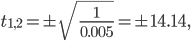
sowie Minima und Maxima gefunden bei
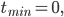
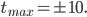
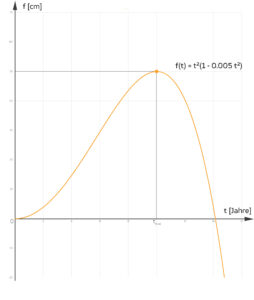
Laut Aufgabenstellung soll dann der Bereich [0, tmax] als „Wachstums“-/Höhenfunktion des Bonsais interpretiert werden. Dieser Mathe-Abi-Bonsaibaum wächst also (entsprechend der Funktion f) im 1. Jahr nur knapp 1 cm, nach dem 2. Jahr ist er ca. 4 cm hoch und nach 10 Jahren hat er 50 cm erreicht? So langsam am Anfang und so „hoch“ nach 10 Jahren? Schnell besucht Rike einige gängige Bonsai-Ratgeberseiten und findet, dass Bonsais im Allgemeinen schnell wie normale Bäume wachsen und nach einigen Jahren in ein kleineres Gefäß umgetopft werden, dass sowohl die Wurzeln als auch Äste beschnitten werden. „Totholz“ ist eine weitere Methode der „Ästhetik“ und der Wachstumsschwächung. Der Stamm wird gern für ein besonders dekoratives Aussehen gebogen. Um die Blätter klein zu halten, werden sie im Sommer entfernt, damit wird ein neues, minderes Wachstum angeregt. Mit anderen Worten, das Wachstum wird von Menschen bestimmt und unterliegt stark ihrer Willkür. Wichtiges Ziel der Bonsai-Züchtung ist eine kleine, filigrane, dekorative Gestalt des Baumes. Es gibt Bonsaibäume, die über 60 Jahre alt und über 1 m hoch sind (für ca. 2.200 € sind sie zu haben). Das hat Rike nach kurzer Zeit recherchiert. Sie ist zwar schockiert wegen der Gewalt, die man den Bonsaibäumen antut und wegen der Werkzeuge, die man dafür benutzt, dennoch ist sie fasziniert von der Schönheit mancher Bonsaibäume. Sie überlegt, wie lang wohl ein Stamm werden kann, wenn man ihn hin- und herwindet. Könnte sie 50 cm Stammlänge erreichen, obgleich der Baum nur 30 cm hoch ist? Wie könnte sie das mathematisch beschreiben?
Modellierung der Geometrie eines gewundenen Bonsaibaumes
Sie möchte die Geometrie des Stammes in 2 Koordinaten beschreiben:
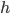… Stammhöhe in cm
… horizontale Koordinate eines Punktes P des Stammes
Dieser Punkt P hat die Koordinaten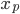 
und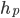 
:
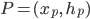
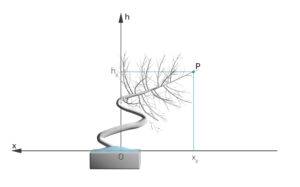
Sie überlegt, wie sie eine Funktion für die Geometrie finden kann und sieht schnell, dass
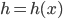
keine Funktion ergibt, es wäre besser, eine Funktion
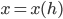
zu suchen und das Koordinatensystem zu drehen. Dann hat der Punkt P die Koordinaten in umgekehrter Reihenfolge:
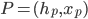
So beginnt sie mit einer Sinuskurve für die Schwingung:
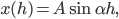
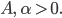
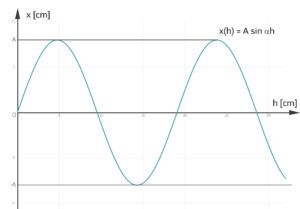
Der Sinus muss natürlich noch nach unten verschoben werden, zum Beispiel so:
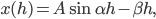
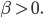
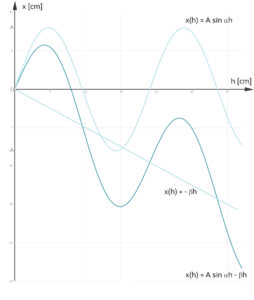
A = 8, α = 0.33, β = 0.5.
Die Funktion x in zeitlicher Abhängigkeit
Rike findet heraus, dass ein Wachstum von 30 cm in 15 Jahren ein guter Wert ist. Zunächst nimmt sie an, dass der Baum gleichmäßig wächst. Tatsächlich ist das Wachstum nicht gleichmäßig, da er ja mehrfach gestutzt und beschnitten wird. Aber mit einem einfachen Ansatz kann sie starten. So erhält sie die Transformation für ein mittleres Wachstum von
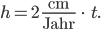
Damit ändert sich die Funktion x jetzt in Abhängigkeit von t:
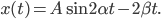
Die Bogenlängenformel
Um die Länge einer Kurve zu berechnen, kann man eine sogenannte Bogenlängenformel benutzen. Diese kann mit den Methoden der Differenzial- und Integralrechnung hergeleitet werden. Im Kern benutzt sie eine Näherung für die Länge eines Kurvenstückes durch eine Tangente und deren Berechnung mit dem Satz des Pythagoras.
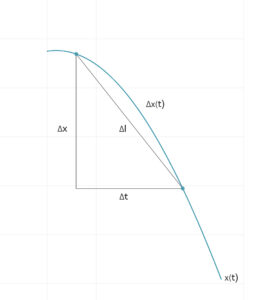
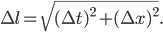
Daraus erhält Rike durch Ausklammern von Δt:
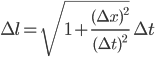
und durch Aufsummieren aller Teilstücke und Grenzübergänge schließlich die Bogenlängenformel
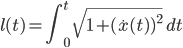
Berechnung der Stammlänge
Die Ableitung einer zeitabhängigen Funktion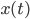 
nach der Zeit wird mit einem Punkt über der Funktion bezeichnet: 
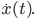Die Ableitung 
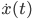von 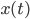kann Rike leicht bestimmen
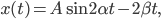
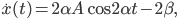
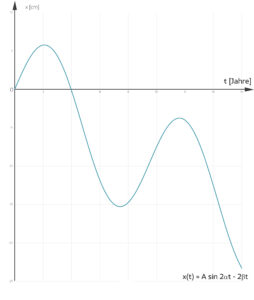
aber das Integral für die Bogenlänge löst sie numerisch für feste Parameter A, α, β mit der Rechteckformel:
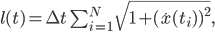
dabei sind ti für i = 1,2, ... , N die Stützstellen aus dem Intervall [0, t] und Δt ihre Schrittweite. So erhält sie die folgende Kurve:
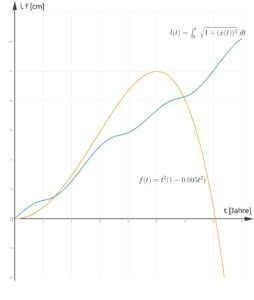
Da kommt Charly zur Tür herein und wundert sich, was Rike an ihrem Notebook macht. Sie erklärt ihm ihre alternative Bonsai-Aufgabe und Lösung.
Charly Da hast du ja einen Bonsaibaum mit einer Stammlänge von 50 cm kreiert, der nach 14 Jahren nur 28 cm hoch ist, nicht schlecht! Ich denke, das können meine Schülerinnen und Schüler auch schaffen, wenn wir die Formel für die Bogenlänge vorher besprechen, ich müsste nur ein Tabellenkalkulationsprogramm als Hilfsmittel zulassen.
Rike Ja, das braucht man.
Charly Rike, kann ich dir eine Freude machen? Ich schenke dir so einen Bonsai, wie du ihn berechnet hast!
Rike Ach nein, danke! Mir würde es das Herz brechen, wenn ich so einen verdrahteten Baum auspacken soll.
Charly Na, dein Herz soll nicht zerbrechen!
Rike Charly, besser wäre doch, einen „normalen“ Baum zu pflanzen.
Charly Okay, das machen wir.
***
Übungsaufgaben
- Teste Rikes Ansatz für andere Parameter A, α und β!
- Wie verändert sich die Kurve für die Bogenlänge, wenn das Wachstum nicht gleichmäßig ist?