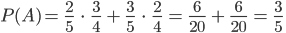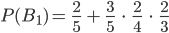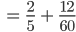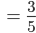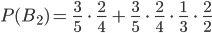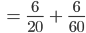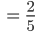Für Charly sind die Sommerferien zu Ende, er unterrichtet wieder Mathe und trainiert eine Volleyballmannschaft. In diesem Schuljahr soll er sogar das Mathe-Abi betreuen. Doch die Lösung einer Statistikaufgabe aus dem Jahr 2020 versteht er nicht und fragt Rike.
Charly Rike, schau mal hier, diese Statistikaufgabe mit den 3 roten und 2 grünen Kugeln verstehe ich nicht, also die Aufgabe schon, aber nicht die Lösung. Wo kommt denn bei a) die blaue Kugel her? Wieso darf im 3. Zug ebenfalls keine Kugel gezogen werden?
Rike Haha, ist ja witzig! Ändern sich die Kugeln? Ziehen einer Kugel ohne Kugel? Sehr merkwürdig.
Die Abitur-Aufgabe von 2020 in Berlin-Brandenburg
1.5 Stochastik
Eine Urne enthält zwei grüne und drei rote Kugeln.
a) Es werden zwei Kugeln nacheinander gezogen. Bestimmen Sie die Wahrscheinlichkeit dafür, dass die gezogenen Kugeln unterschiedliche Farben haben.
b) Die gezogenen Kugeln werden zurück in die Urne gelegt. Nun werden von zwei Personen solange Kugeln nacheinander entnommen bis eine grüne Kugel gezogen wurde. Zeigen Sie, dass die Person, die anfängt, das Spiel eher gewinnt.
Lösung
a) Es wird nacheinander und ohne Zurücklegen gezogen. Entsprechend ändern sich die Wahrscheinlichkeiten mit jedem Zug. Für zwei verschieden farbige Kugeln müssen zuerst eine grüne und dann eine rote () oder zuerst eine rote und dann eine blaue Kugel (
) gezogen werden.
b) Da nur drei rote Kugeln in der Urne sind, wird spätestens im vierten Zug die erste grüne Kugel gezogen.
Die anfangende Person erhält somit den 1. und 3. Zug. Um zu gewinnen, muss sie also direkt die grüne Kugel (
) im ersten Zug ziehen oder in den ersten beiden Zügen werden von beiden Personen je eine rote (
) und anschließend im dritten die grüne gezogen.
Die zweite Person müsste hingegen darauf hoffen, dass im ersten Zug keine grüne Kugel gezogen wird und sie selbst im zweiten dann die grüne zieht. Ansonsten darf im dritten Zug ebenfalls keine Kugel gezogen werden.
Es gilt:
und somit hat die erste Person einen Vorteil zu gewinnen.
[Mathematik Abitur 2022, S. 38 f., 48 f., Hervorhebungen durch uns]
Rike Eigentlich ist es traurig. In der Mathematik gibt es so viele Methoden, um Missverständnisse zu vermeiden, ja, die ganze formale mathematische Schreibweise versucht, sehr korrekt zu sein und vermeidet die Umgangssprache. In der Wahrscheinlichkeitstheorie müssen die Ereignisse, für die die Wahrscheinlichkeiten berechnet werden, klar und unmissverständlich beschrieben werden, am besten gleich so, dass man sie codieren kann.
Charly Jaja, hier wird mit dem Vorgang des Kugelziehens argumentiert, die Berechnung bleibt unklar.
Lösung der Aufgabe a): Zwei verschieden farbige Kugeln
Rike Lass uns für die Aufgabe a) die beiden Ereignisse 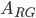 und
und 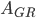 formulieren:
formulieren:
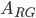 … es wird zuerst eine rote und dann eine grüne Kugel gezogen
… es wird zuerst eine rote und dann eine grüne Kugel gezogen
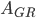 … es wird zuerst eine grüne und dann eine rote Kugel gezogen
… es wird zuerst eine grüne und dann eine rote Kugel gezogen
Beide Ereignisse ergeben zusammen das Ereignis A:
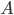 … es werden 2 verschieden farbige Kugeln gezogen
… es werden 2 verschieden farbige Kugeln gezogen
Charly Gute Idee. Es ist
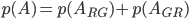
Rike Richtig. Und jetzt machen wir eine Art Baumdiagramm dafür:
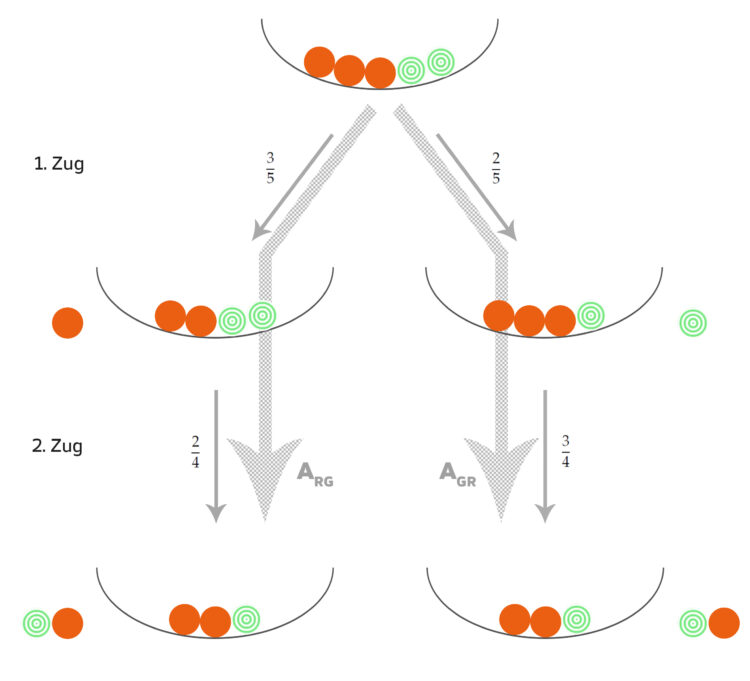
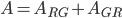
Charly Schön. Jetzt sehe ich, wie sich die Wahrscheinlichkeiten der einzelnen Ereignisse berechnen:
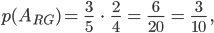

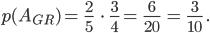
Also
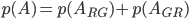

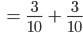

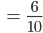

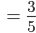
Lösung der Aufgabe b): Wer zieht zuerst eine grüne Kugel?
Rike Und jetzt noch die Aufgabe b). Ich zeichne mal das Baumdiagramm, dann finden wir die entsprechenden Ereignisse:
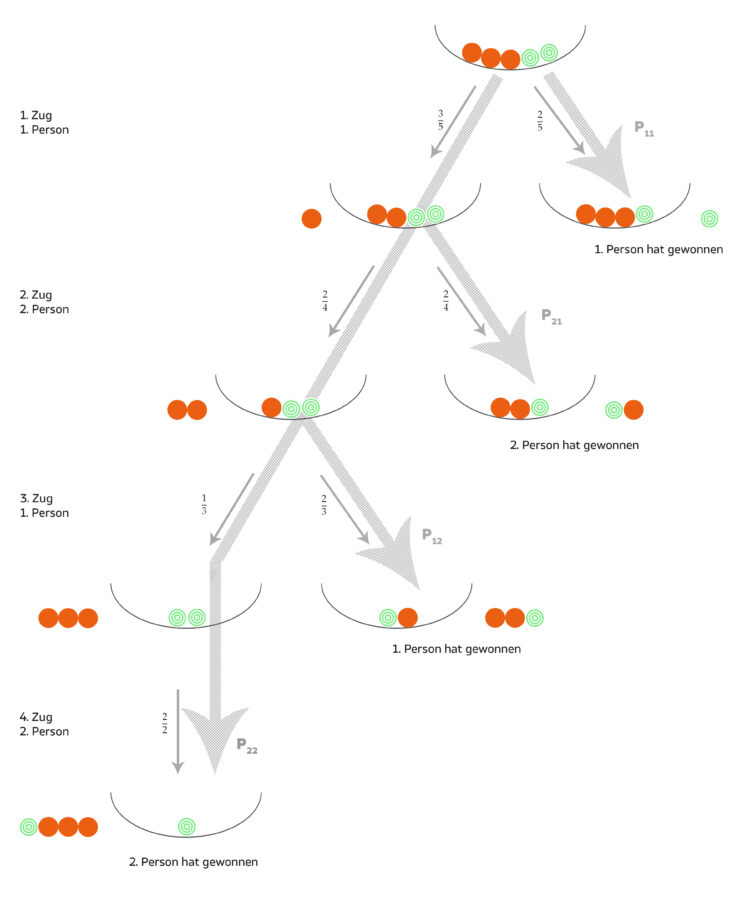
Charly Okay, jetzt sieht Alles so klar aus, danke, Rike. Also die wichtigsten Ereignisse wären dann
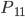 … die 1. Person gewinnt im 1. Zug (durch Ziehen einer grünen Kugel)
… die 1. Person gewinnt im 1. Zug (durch Ziehen einer grünen Kugel)
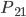 … die 2. Person gewinnt in ihrem 1. Zug (durch Ziehen einer grünen Kugel)
… die 2. Person gewinnt in ihrem 1. Zug (durch Ziehen einer grünen Kugel)
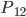 … die 1. Person gewinnt in ihrem 2. Zug (durch Ziehen einer grünen Kugel)
… die 1. Person gewinnt in ihrem 2. Zug (durch Ziehen einer grünen Kugel)
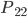 … die 2. Person gewinnt in ihrem 2. Zug (durch Ziehen einer grünen Kugel)
… die 2. Person gewinnt in ihrem 2. Zug (durch Ziehen einer grünen Kugel)
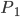 ... die 1. Person gewinnt (, weil sie als 1. eine grüne Kugel zieht)
... die 1. Person gewinnt (, weil sie als 1. eine grüne Kugel zieht)
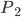 … die 2. Person gewinnt (, weil sie als 1. eine grüne Kugel zieht)
… die 2. Person gewinnt (, weil sie als 1. eine grüne Kugel zieht)
Rike Schön!
Charly Jetzt berechne ich die einzelnen Wahrscheinlichkeiten dafür, eigentlich schreibe ich sie nur auf, sie ergeben sich direkt aus dem Baumdiagramm:
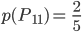

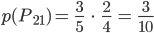

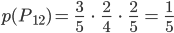

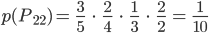
Richtig?
Rike Richtig!
Charly Weiter, die 1. Person kann in ihrem 1. oder 2. Zug gewinnen:
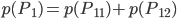

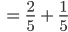

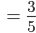
Genauso geht das für die 2. Person:
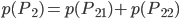

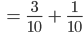

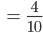

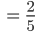
Die Wahrscheinlichkeit 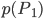 ist größer als
ist größer als 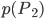 :
:
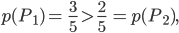
also ist das Spiel nicht fair, die 1. Person hat einen Vorteil.
Rike Stimmt! War ja nicht so schwer, du kannst es gut erklären.
Charly Danke!
***
Übungsaufgabe
Wie könnte eine faire Urnenaufgabe aussehen?