Rike und Ben sind immer noch am Nord-Ostsee-Kanal bei Brunsbüttel. Hinter jedem Schiff bilden sich Wellen. Diese genügen der Navier-Stokes-Gleichung – und die ist immer noch eine Herausforderung. Recht einfach sind gleichmäßige Wellen in einer Richtung zu verstehen. Sie bilden eine spezielle Lösung dieser Gleichung. Rike konstruiert auch noch einen passenden Hilbertraum dafür.
Navier-Stokes-Gleichungen
Rike Ben, hier kannst du mal partielle Differenzialgleichungen in echt erleben, die Navier-Stokes-Gleichungen!
Ben Navier-Stokes?
Rike Ja, Navier-Stokes! Die beschreiben die Bewegungen einer Flüssigkeit:
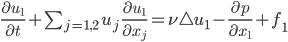
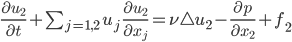
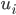… Geschwindigkeitskomponente der Flüssigkeit in die i-te Richtung, i=1, 2
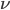… positiver Koeffizient für die Viskosität der Flüssigkeit
… der Laplace-Operator
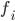… die i-te Komponente der äußeren Anregung, i=1, 2
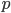… der hydrodynamische Druck der Flüssigkeit
Ben Nichtlineare partielle Differenzialgleichungen?
Rike Stimmt! Kleiner geht’s nicht! Damit auch wirklich Flüssigkeiten beschreiben werden, soll das Geschwindigkeitsfeld divergenzfrei sein:
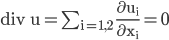
Ben Hat man denn da überhaupt eine Chance?
Rike Gute Frage. Es gibt sehr viel Literatur und Teilergebnisse, es gibt Experimente und ein paar interessante Phänomene. Ja, es ist sogar ein Preis ausgelobt worden, einer von den Millenium-Preisen des Clay Institutes.
Ben Aha! Und den willst du gewinnen? Ich soll das programmieren? Mit AI die Phänomene erkennen und die Wirkung vorhersagen?
Rike Ja! Genau! Haha.
Ben Okay, was sind denn die mathematischen Grundlagen, Rike?
Rike Schau mal hier, der Nord-Ostsee-Kanal! Hier haben wir ein beschränktes, zweidimensionales Gebiet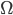 
. Bei Brunsbüttel und in Kiel sind Schleusen, dort treffen die Wellen auf harte Widerstände und reflektieren total, da könnten wir fordern, dass die Änderung der Geschwindigkeit in Normalenrichtung zur Schleuse verschwindet:
Homogene Randbedingungen 2. Art
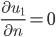
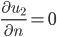
für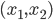 
am Ende bei den Schleusen.
Bei den normalen Ufern rechts und links entlang des Kanals müssen wir uns das Verhalten der Wellen überlegen.
Ben Hmm, der Kanal ist nicht breit genug, dass die Geschwindigkeiten an den Ufern verschwinden – und totale Reflexion ist es auch nicht. Dann eben so ein Mix.
Rike Stimmt, nehmen wir Randbedingungen 3. Art. Die Koeffizienten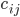 
kriegen wir durch Vergleich von Simulation und Praxis.
Randbedingungen 3. Art
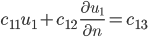
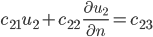
Ben Klar, das mache ich dann!
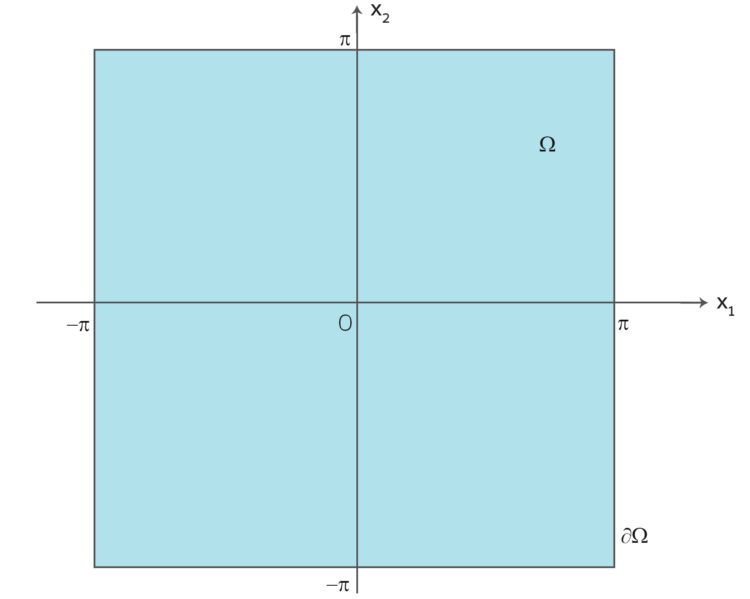
Rike In der Theorie werden einfachere Gebiete und Randbedingungen untersucht. Wenn der Nord-Ostsee-Kanal so eine quadratische Form hätte und wenn an den Ufern periodische Randbedingungen herrschen:
Periodische Randbedingungen
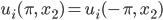
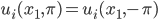
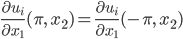
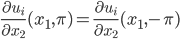
Ben Hmm?
Rike Ach, das heißt nur, dass rechts und links dieselben Funktionswerte an den Ufern sind, ebenso oben und unten – und auch dieselben Ableitungen in Normalenrichtung.
Ben Okay, aber dieses Quadrat und die periodischen Randbedingungen haben doch nichts mehr mit dem Nord-Ostsee-Kanal zu tun!
Rike Stimmt! Willst du nun die Ergebnisse hören oder nicht?
Ben Na, gut, dann leg mal los!
Eine stationäre Lösung
Rike Also, im quadratischen Gebiet gibt es die stationäre Lösung
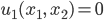
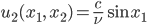
mit
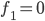
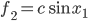
ist eine positive Konstante.
Ben Aha, eine Schwingung des Geschwindigkeitsfeldes in eine Richtung, angeregt durch eine äußere Schwingung in dieselbe Richtung? –
Ein Hilbertraum für den Nord-Ostsee-Kanal
Rike Siehst du, ist ja gar nicht schlecht, fast wie bei uns hier auf dem Boot. Jetzt lass uns weitermachen. Wir nehmen also den echten Nord-Ostsee-Kanal und unsere Randbedingungen mit der Reflexion an den Schleusen und Randbedingungen dritter Art an den Ufern. Dann gibt es so ein Standard-Tool zu Lösung der Navier-Stokes-Gleichungen, dass man den passenden Raum dafür sucht.
Ben Ein Hilbertraum?
Rike Genau!
Ben Und der wäre?
Rike Na, wir nehmen der Raum der quadratisch integrierbaren Funktionen über dem Gebiet 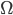des Nord-Ostsee-Kanals und über einem endlichen Zeitintervall 
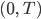, die außerdem noch einmal differenzierbar sind und deren Ableitung auch wieder quadratisch integrierbar ist:
Das Skalarprodukt wäre dann
Der Raum heißt übrigens Sobolev-Raum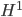 
. Die 1 kommt von der Forderung, dass die Funktionen nur einmal differenzierbar sein sollen.
Ben Okay. Wie bringt uns das weiter?
Rike Aus den Navier-Stokes-Gleichungen machen wir im Hilbertraum neue Gleichungen. Wir nehmen nun sogenannte Testfunktionen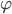 
aus einem Unterraum desselben Hilbertraums, die beliebig differenzierbar sind, am Rand des Gebietes 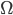zu Null werden und divergenzfrei sind:
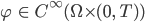
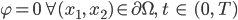
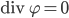
Mit solchen 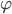-Testfunktionen multiplizieren wir die Navier-Stokes-Gleichungen, haben am Rand überhaupt keine Schwierigkeiten und integrieren über 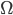und das Zeitintervall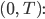 
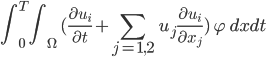
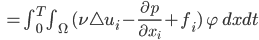
i=1, 2.
Jetzt kannst du die Formeln der partiellen Integration anwenden.
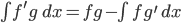
Finale Gleichungen
Und schließlich kriegst dann die finalen Gleichungen
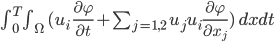
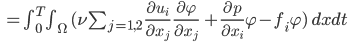
Ben Aha! Und ich soll das numerisch lösen! Mit verschiedenen Testfunktionen 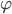? Okay, ich brauche die digitale Karte des Kanals und ein paar typische Anregungen 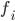, wie eben die Schiffe hier fahren und ihre Geometrie, dann kann ich das versuchen!
Rike Super, Ben, du bist der Größte! Das Preisgeld können wir ja teilen.
Ben Haha!
***
Übungsaufgaben
- Überprüfe die spezielle Lösung im Quadrat. Wie groß ist ?
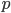- Überprüfe die Umwandlung der Navier-Stokes-Gleichungen in die Skalarprodukt-Formulierung.
- Welche Vorteile bietet die Hilbertraum-Lösung gegenüber einer klassischen Lösung?
Lösungen
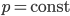
- OK
- Die Hilbertraum-Lösungen müssen nur einmal bzgl. des Ortes differenzierbar sein. Das ergibt eine viel größere Lösungsmenge und viel mehr Tools in Hilbert- und Sobolev-Räumen. Allerdings ist die physikalische Interpretation solcher schwacher Lösungen umstritten.