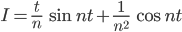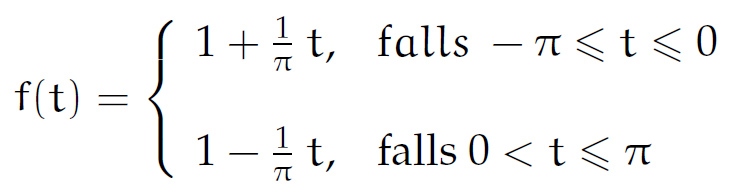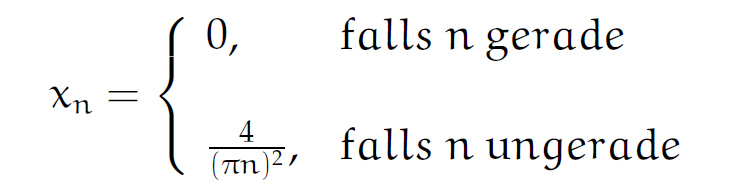Rike und Ben müssen einfach mal aus Berlin raus. Sie fahren in den Norden. Als sie am Nord-Ostsee-Kanal in Brunsbüttel ankommen, bewundern sie die großen und die kleinen Schiffe. Rike fallen sofort die Wellen am Bug der Schiffe auf. Sie erklärt Ben, dass man Funktionen, die man normalerweise nicht als Schwingungen versteht, durch Schwingungen nähern kann.
Rike Ben, weißt du, man kann ziemlich viele Funktionen durch Schwingungen annähern, auch wenn sie gar keine Schwingungen sind.
Ben Hmm.
Nichtdifferenzierbare Funktionen
Rike Vor allem, wenn sie nicht differenzierbar sind, kann man sie doch durch Sinus- und Kosinusfunktionen ausdrücken.
Ben Hmm.
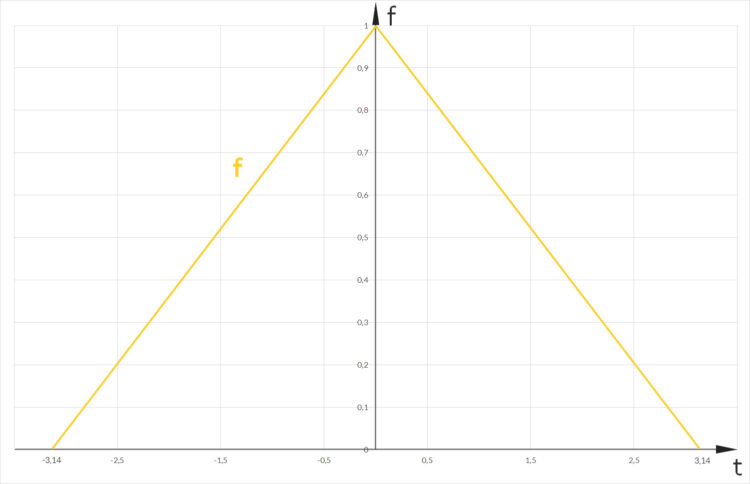
Rike Lass uns mal die Dreiecksfunktion über 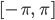 nehmen:
nehmen:
Orthonormalsystem aus Sinus- und Kosinusfunktionen
Mit den Sinus- und Kosinusfunktionen und der Konstanten kriegen wir wieder ein Orthonormalsystem im Raum 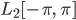 .
.
Ben  ?
?
Rike Na, der Raum der quadratisch integrierbaren Funktionen über dem Intervall  .
.
Ben Ach, schon wieder die Fourier-Reihe!
Rike Stimmt. Ich denke, ich kann hier alle Fourier-Koeffizienten berechnen.
Ben Na, dann mal los!
Der konstante Anteil der Dreiecksfunktion
Rike Zu der konstanten Funktion
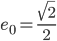
kriege ich den Koeffizienten:
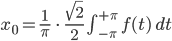
Weil
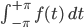
gerade die Fläche unter dem Dreieck ist, nennen wir die mal 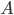 , dann ist die Fläche
, dann ist die Fläche 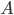 aus geometrischen Überlegungen:
aus geometrischen Überlegungen:
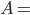
Also ist
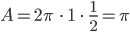
und
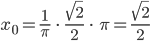
Ben Okay.
Die Kosinusanteile der Dreiecksfunktion
Rike Wegen der Symmetrie der Dreiecksfunktion werden alle Sinusanteile zu Null und so haben wir nur die Kosinusanteile. Ich schreibe mal für die  -te Fourierreihe:
-te Fourierreihe:
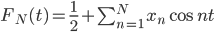
und die Koeffizienten  kriege ich mit dem Skalarprodukt der Dreiecksfunktion mit den Kosinusfunktionen aus dem Orthonormalsystem:
kriege ich mit dem Skalarprodukt der Dreiecksfunktion mit den Kosinusfunktionen aus dem Orthonormalsystem:
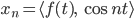
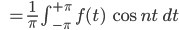
für 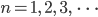
Die Symmetrie der Dreiecksfunktion hilft uns schon wieder: Es reicht, wenn wir nur von 0 bis 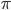 integrieren:
integrieren:
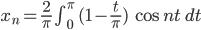
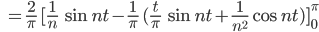
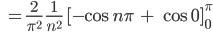
Dafür habe ich 2 Fälle:
Die Fourierreihe zum Dreieck
Ben Hey, Rike, du hast’s geschafft! Alle Fourierkoeffizienten!
Rike Ja! So kann ich die Dreiecksfunktion als Summe von Kosinusfunktionen schreiben:
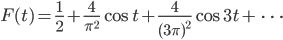
Ben Okay, das kann ich zeichnen:
Konvergenz der Zerlegung
Aber sag mal, Rike, an der Spitze bei Null sehe ich keine Konvergenz, und am Rand – bei 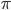 und
und 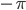 auch nicht! Die Überlagerung von Sinus- und Kosinus werden niemals eckig werden!
auch nicht! Die Überlagerung von Sinus- und Kosinus werden niemals eckig werden!
Rike Du hast Recht, die Theorie gibt keine punktweise Konvergenz her. Die Konvergenz der Reihe 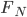 zur Dreiecksfunktion
zur Dreiecksfunktion  :
:
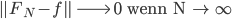
funktioniert natürlich nur in der Norm des Hilbertraumes, also im quadratischen Mittel.
Das quadratische Mittel
Ben Unendlich viele Kosinusfunktionen ergeben im quadratischen Mittel eine Dreiecksfunktion?
Rike Ja, schau mal, die Differenz ist wirklich nicht groß:
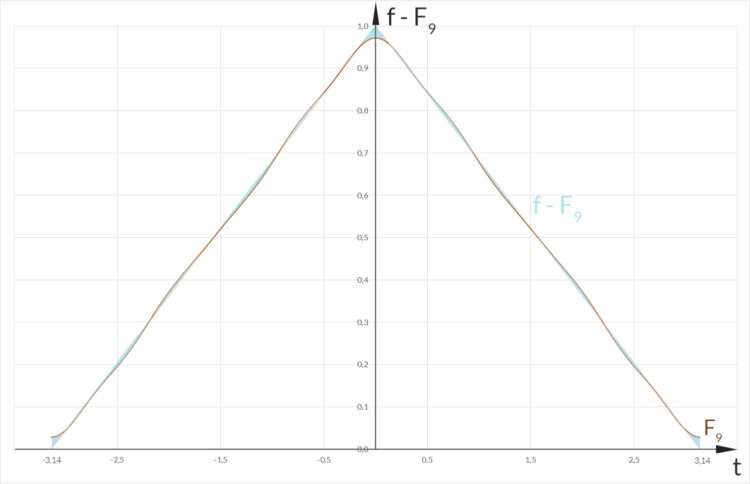
 als hellblaue Fläche
als hellblaue Fläche
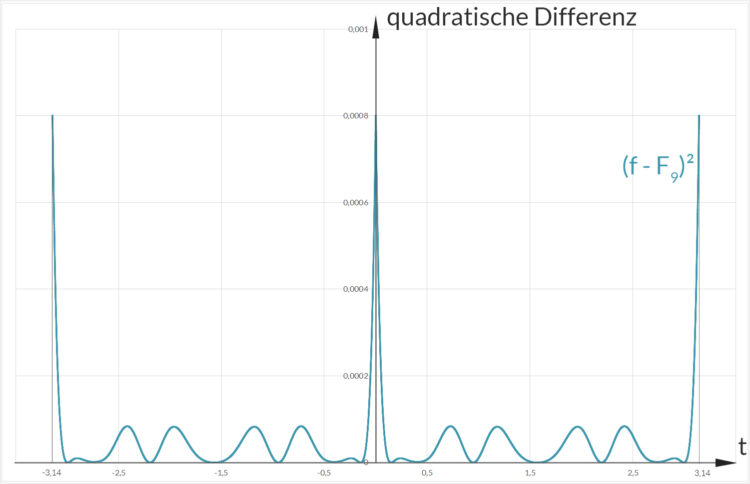
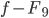
Dann kannst du dir vorstellen, dass die Fläche unter der quadratischen Differenz nach Null geht:
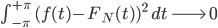
Ben Na, okay, deine Koeffizienten 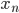 werden ja quadratisch kleiner, da brauche ich nicht lange zu rechnen, um an die Rechnergenauigkeit zu kommen. Mich wundert immer noch, dass unendlich viele Überlagerungen von etwas Rundem etwas Eckiges ergeben – eben gerade die gegenteilige Eigenschaft. Liegt das am Hilbertraum oder an meinem naiven Verständnis von Mathematik?
werden ja quadratisch kleiner, da brauche ich nicht lange zu rechnen, um an die Rechnergenauigkeit zu kommen. Mich wundert immer noch, dass unendlich viele Überlagerungen von etwas Rundem etwas Eckiges ergeben – eben gerade die gegenteilige Eigenschaft. Liegt das am Hilbertraum oder an meinem naiven Verständnis von Mathematik?
Rike Haha!
***
Übungsaufgabe
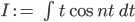
Lösung