Rike erzählt Ben wieder von ihren Entdeckungen im Hilbertraum.
Rike Weißt du, diese Hilberträume mit Orthonormalsystemen 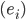 , Skalarprodukt
, Skalarprodukt 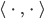 und dem schönen Zerlegungssatz für jeden Vektor
und dem schönen Zerlegungssatz für jeden Vektor 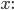
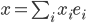
mit
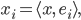
die findest du nicht nur im Zwei- oder Dreidimensionalen. Du als Informatiker hast ja viel mit längeren Arrays zu tun…
Ben Klar! Gerade bei AI müssen wir tausende Parameter verarbeiten. Klar könnten wir Arrays als Vektoren im Vektorraum auffassen – und wenn du willst, auch im Hilbertraum.
Rike Ja, das wäre nicht schlecht! Das Skalarprodukt wäre
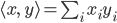
im Reellen und
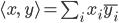
im Komplexen.
Ben Okay.
Rike Stell dir vor, um die Differenz zweier Arrays im Hilbertraum zu berechnen, könnte man die Norm
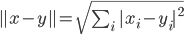
benutzen.
Ben Klar.
Der Folgenraum l2
Rike Nun stell dir vor, die Arrays werden immer länger, die Raumdimension  wird immer größer – und schließlich ist
wird immer größer – und schließlich ist  nicht mehr zu beschränken und festzulegen.
nicht mehr zu beschränken und festzulegen.
Ben Der Horror für alle Informatiker!
Rike Ja, also du hast dann Folgen mit unendlich vielen Komponenten.
Ben Super!
Rike Neben der Vektorraumstruktur und dem Skalarprodukt
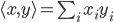
im Reellen oder
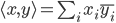
im Komplexen muss man noch fordern, dass für jede Folge 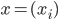 das Skalarprodukt mit sich selbst und folglich auch die Norm
das Skalarprodukt mit sich selbst und folglich auch die Norm
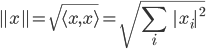
konvergiert.
Ben Richtig.
Rike Okay, damit haben wir den Raum 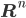 bzw.
bzw. 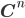 verallgemeinert zu einem Folgenraum der quadratisch integrierbaren Folgen, der
verallgemeinert zu einem Folgenraum der quadratisch integrierbaren Folgen, der 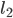 .
.
Ben Okay.
Rikes Signalaufgabe
Rike Jetzt stell dir vor, du als Informatiker, kriegst eine Zahlenfolge geliefert, eine Art Information oder Signal:
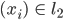
Du sollst dazu einen Vektor
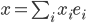
in einem geeigneten Hilbertraum mit einem geeigneten Orthonormalsystem finden!
Ben Haha! Das Signal aus einem fremden Universum! Ich kriege unendlich viele Informationen und soll daraus ein einziges Element konstruieren? Ist das ein Paradoxon?
Rike Haha, nein, nein. Also lass uns mal die Folge 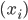 mit
mit
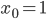
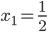
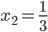

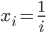

nehmen. Die ist quadratisch summierbar.
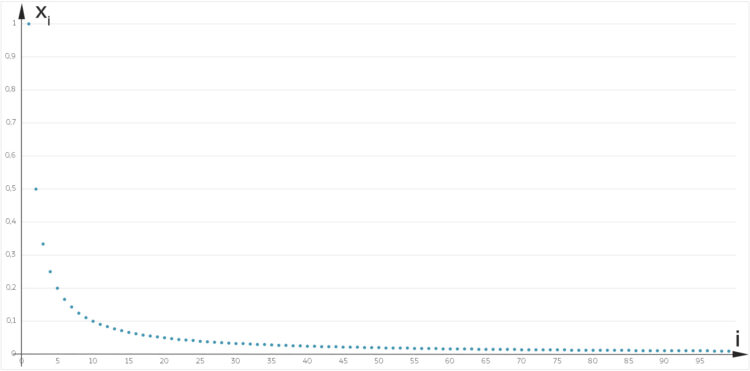
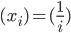
Ben Okay, das ist schon mal was, dass nicht Alles voll daneben geht.
1. Die Fourier-Reihe aus der Folge
Rike Und als Hilbertraum nehmen wir mal den Raum der quadratisch integrierbaren Funktionen mit periodischen Randbedingungen über dem Intervall 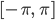 , dem
, dem 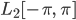 . Die Konstante, die Sinus- und die Kosinusfunktionen bilden ein Orthonormalsystem:
. Die Konstante, die Sinus- und die Kosinusfunktionen bilden ein Orthonormalsystem:
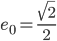
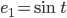
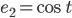
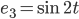
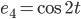
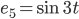

Das Skalarpordukt ist in diesem Raum 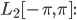
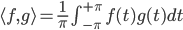
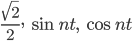
Ben Ah, die Fourier-Reihe!
Rike Richtig, der Raum der Schwingungen. Man versucht, Alles durch Überlagerung von Schwingungen auszudrücken.
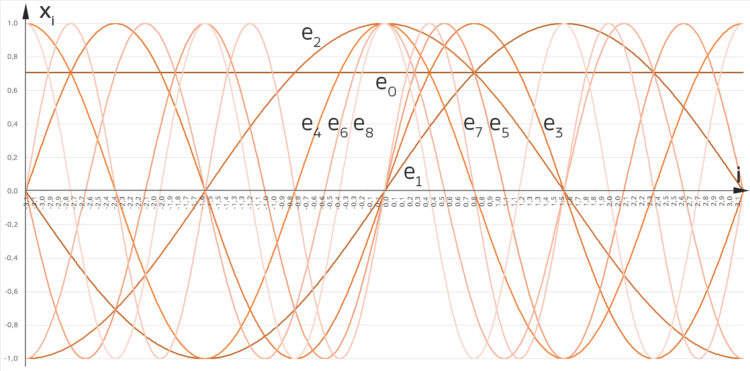
Ben Na gut, ich zeichne mal die Fourierreihe für ein paar Glieder, 9, reicht das, Rike?
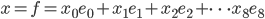
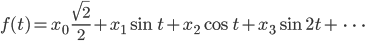
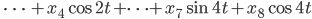
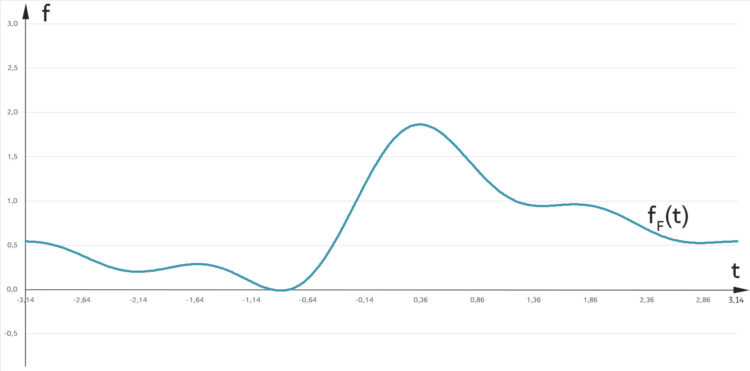
 bis zum 9. Glied
bis zum 9. GliedRike Okay, Ben, ist ein kleiner Anfang!
2. Die Tschebyschew-Reihe aus der Folge
Ben Aber sag mal, ist das der einzige Funktionenraum?
Rike Hey, Ben! Das ist der Punkt, die gegeben Zahlenfolge 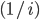 kann auch in einem anderen Raum interpretiert werden. Zum Beispiel bilden die Tschebyschew-Polynome auch ein Orthogonalsystem im Raum der quadratisch integrierbaren Funktionen über [-1, 1], dem
kann auch in einem anderen Raum interpretiert werden. Zum Beispiel bilden die Tschebyschew-Polynome auch ein Orthogonalsystem im Raum der quadratisch integrierbaren Funktionen über [-1, 1], dem 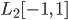 . Das Skalarprodukt ist dann
. Das Skalarprodukt ist dann
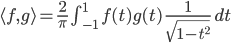
Ben Hmm, schon anspruchsvoller zu integrieren!
Rike Stimmt! Aber das Gute, die Polynome berechnen sich rekursiv, du brauchst also nicht so große Potenzen zu berechnen.
Ben Okay, ein Hoffnungsschimmer.
Rike Die Tschebyschew-Polynome sehen so aus:
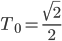
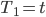
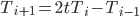
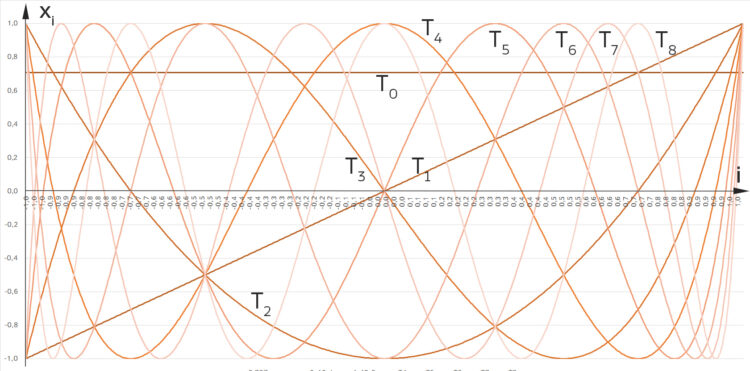
Ben Gut, dann versuche ich mal, die 9. Näherung
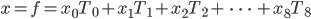
zu zeichnen.
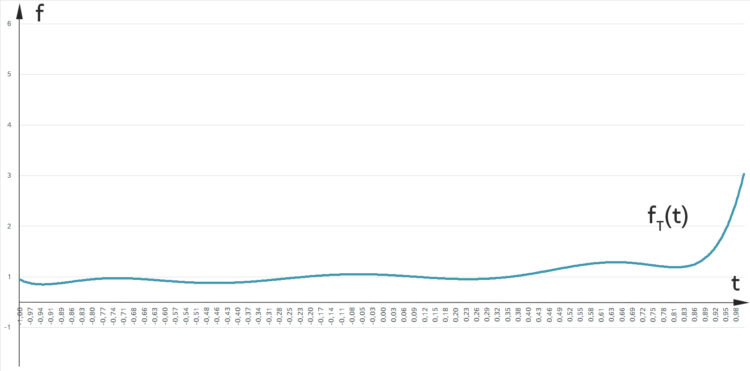
 aus derselben Folge
aus derselben Folge 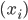 mit Tschebyschew-Polynomen
mit Tschebyschew-PolynomenHier, Rike! Dieses  ist jetzt nicht periodisch, es sieht fast wie eine Corona-Kurve aus!
ist jetzt nicht periodisch, es sieht fast wie eine Corona-Kurve aus!
Rike Nein, deine Kurve wächst nur polynomial, nicht exponentiell!
Der Satz von Fischer & Riesz
Ben Aber sag mal Rike, wenn ich eine Folge 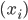 bekomme und einen Hilbertraum
bekomme und einen Hilbertraum 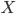 mit Skalarprodukt und Orthonormalsystem
mit Skalarprodukt und Orthonormalsystem 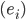 , dann müsste doch die Zuordnung
, dann müsste doch die Zuordnung
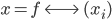
eineindeutig sein? Aus der Folge kriegst du die Funktion
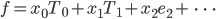
und umgekehrt, aus der Funktion  kriegst du mit
kriegst du mit
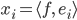
die Zuordnung zur Folge 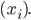
Rike Hey, Ben, du hast gerade den Satz von Fischer & Riesz gefunden – nur leider 100 Jahre zu spät!
Ben Haha!
Übungsaufgaben
Überprüfe die Orthonormalität einiger Funktionen:
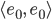
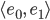
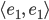
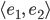
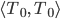
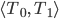
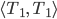
Lösungen
1, 0, 1, 0, 1, 0, 1
