Rike erzählt Ben weitere Anekdoten aus ihrer Kindheit.
Rike Wir hatten also Koordinatensysteme und Vektoren bei Wiezorek, wir haben die Länge von Vektoren nach dem Satz des Pythagoras berechnet, haben immerzu kleine mechanische Aufgaben gerechnet, wo man Vektoren für die resultierende Kraft addieren musste, und schließlich kamen Aufgaben, wo die Projektion einer Kraft auf eine Gerade berechnet werden sollte.
Wiezoreks Einführung des Skalarproduktes
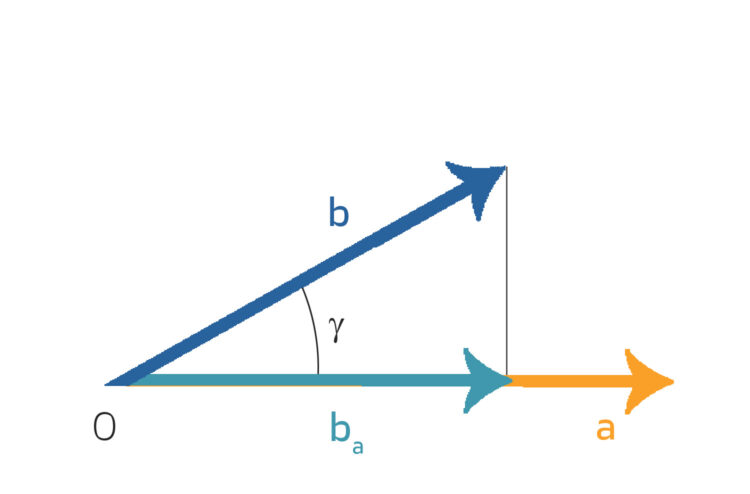
Autos, die den Berg hochfahren, Gärtner, die einen Rasenmäher schieben oder Pferde, die einen Wagen mit einem Ritter zogen und die Neigung der Deichsel bekannt war. Lauter unerschrockene Helden, die die Welt jeden Tag besser machen!
Ben Haha! Jetzt bist du aber sehr streng!
Rike Ah! Dann kam der Tag, an dem Wizorek uns die Arbeit erklärte: Als die Kraft 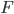 , die auf einen Weg
, die auf einen Weg 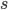 projiziert wurde, multipliziert mit der Länge des zurückgelegten Weges:
projiziert wurde, multipliziert mit der Länge des zurückgelegten Weges:

Naja, dieses 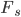 kannst du berechnen, wenn du den Winkel
kannst du berechnen, wenn du den Winkel 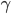 und die Länge des Vektors
und die Länge des Vektors 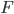 kennst:
kennst:
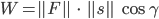
Ben Okay.
Rike Ja, das ist schon klar, aber dieses 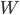 hat Wiezorek als Skalarprodukt von
hat Wiezorek als Skalarprodukt von 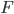 und
und 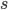 definiert.
definiert.
Ben Ich glaube, wir hatten das auch so ungefähr. Was ist dein Problem?
Rike Er hat das Skalarprodukt als mechanische Arbeit im 2D-Raum definiert! Und was ist, wenn es keine mechanische Arbeit gibt, die Winkel sich nicht messen lassen oder die Räume mehr Dimensionen haben?
Ben Hmm.
Rike Und außerdem ist das Skalarprodukt nicht ein zusätzliches Add on, eine nette kleine geometrische Eigenschaft, die man auswendig lernen soll und für diese Rasenmäher-Auto-Ritter-Aufgaben braucht, sondern ganz fundamental. Wenn man das Skalarprodukt in einem Vektorraum hat, dann und erst dann kann man darin Winkel und Längen messen, Projektionen berechnen und und und ... !!!
Ben Rike, ist ja gut! Wie bist du denn mit Wiezorek klargekommen? Hast du ihn wirklich gefragt, wie er das Skalarprodukt berechnet, wenn es keine mechanische Arbeit gibt oder wenn er keine Winkel zwischen den Geraden hat?
Rike Ja, das habe ich!
Ben Und?
Rike Er ist sehr wütend geworden, hat meine Eltern in die Schule zitiert und mich in die letzte Reihe gesetzt.
Ben Tatsächlich?
Rike Ja!
Ben Und deine Eltern?
Rike Die haben mich in Schutz genommen. Meine Mutter hat mir dann das Skalarprodukt erklärt.
Vektorraum X
Und das geht so: Zunächst braucht man einen linearen Raum 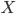 mit Koeffizienten in
mit Koeffizienten in 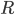 oder
oder 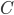 . Meist heißt er auch Vektorraum. In dem sind die Addition von Vektoren, das Vielfache ihrer Vektoren und das Assoziativgesetze erklärt
. Meist heißt er auch Vektorraum. In dem sind die Addition von Vektoren, das Vielfache ihrer Vektoren und das Assoziativgesetze erklärt
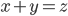
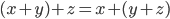
Es gibt einen Nullvektor 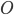 mit der Eigenschaft:
mit der Eigenschaft:
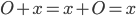
Zu jedem Vektor  gibt es einen negativen Vektor
gibt es einen negativen Vektor 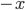 , sodass
, sodass
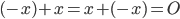
Ben Aaah, 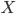 ist eine Gruppe bzgl. der Addition.
ist eine Gruppe bzgl. der Addition.
Rike Okay, du weißt ja gut Bescheid! Außerdem brauchen wir noch ein paar sinnvolle Eigenschaften für die Vielfachen der Vektoren:
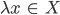
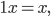
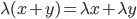
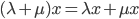
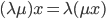
für alle 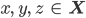 und
und 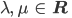 bzw.
bzw. 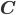 .
.
Ben Okay. Das kann ich mir schon im 2- oder 3-dimensionalen Vektorraum vorstellen.
Rikes Skalarprodukt in X
Rike Ja, richtig. Jetzt kannst du im Vektorraum 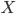 ein Skalarprodukt als Abbildung von zwei Vektoren in die reellen oder komplexen Zahlen:
ein Skalarprodukt als Abbildung von zwei Vektoren in die reellen oder komplexen Zahlen:
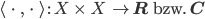
definieren. Es muss die Eigenschaften haben:
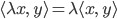
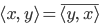
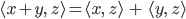
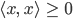
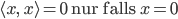
wieder für alle 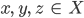 und
und 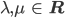 bzw.
bzw. 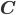 .
.
Ben Na gut, so stelle ich mir das Skalarprodukt auch vor. Ich kenne es meist nur reell, aber okay.
Rike Wenn du das hast, dann hast du auch die „Länge von Vektoren“, nämlich
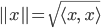
Und für den Abstand zweier Vektoren  und
und  hast du dann als
hast du dann als
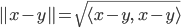
Dieser Abstand erfüllt alle Eigenschaften einer Norm, das freut alle Mathematikerinnen und Mathematiker, denn damit haben sie einen normierten Raum. Das hat Wiezorek natürlich auch in seinem Raum 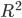 oder
oder 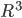 , aber er hat es als Eigenschaft aus der Darstellung von Vektoren genommen.
, aber er hat es als Eigenschaft aus der Darstellung von Vektoren genommen.
Ben Hmm.
Rike Wenn ich jetzt außerdem fordere, dass jede konvergente Folge 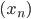 in diesem Raum
in diesem Raum 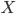 mit dieser Norm auch einen Grenzwert besitzt, dann haben ich einen sogenannten Hilbertraum.
mit dieser Norm auch einen Grenzwert besitzt, dann haben ich einen sogenannten Hilbertraum.
Ben Aha, da ziehst du ja einen großen Bogen: von Descartes mit seinem Koordinatensystem über Euklid mit seiner Geometrie von Punkten, Geraden und dem Parallelenaxiom bis hin zu Hilbert! 2000 Jahre Mathematik!
Orthonormalsystem
Rike Na klar, das muss so schon sein. Und jetzt kommt das Beste! In jedem Hilbertraum kann man ein Orthonormalsystem finden, eine Art Basis. Das sind die Einheitsvektoren auf den Koordinatenachsen. Nennen wir die mal 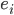 . Die Länge 1 kriegen wir durch die Forderung
. Die Länge 1 kriegen wir durch die Forderung
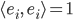
Außerdem müssen immer zwei von ihnen orthogonal aufeinander stehen:
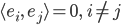
Im 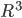 wären das zum Beispiel:
wären das zum Beispiel:
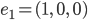
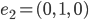
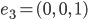
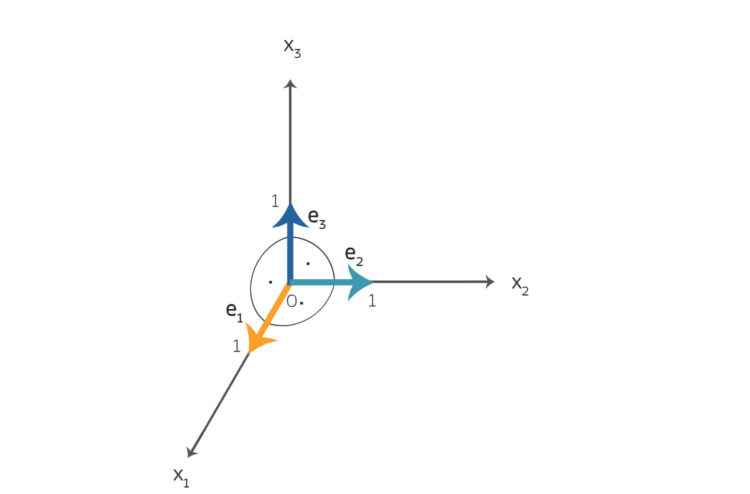
Damit kann man jeden Vektor  im Hilbertraum als Summe dieser Einheitsvektoren mit reellen oder komplexen Koeffizienten darstellen, die man noch dazu sehr leicht mit dem Skalarprodukt ausrechnen kann:
im Hilbertraum als Summe dieser Einheitsvektoren mit reellen oder komplexen Koeffizienten darstellen, die man noch dazu sehr leicht mit dem Skalarprodukt ausrechnen kann:
Zerlegungssatz
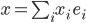
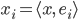
Im 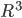 bedeutet das, dass ein Vektor, sagen wir mal
bedeutet das, dass ein Vektor, sagen wir mal
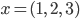
als Summe der Anteile in die 3 Richtungen geschrieben werden kann:
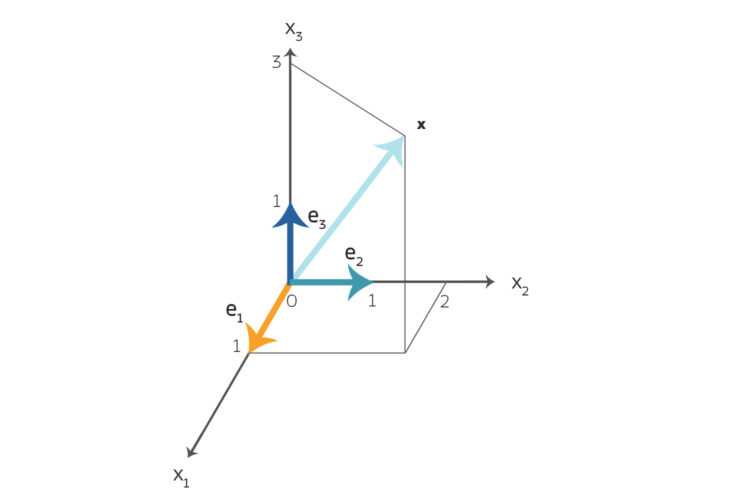
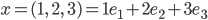
Diese Zahlen vor den Einheitsvektoren kriegst du aus dem Skalarprodukt der Vektoren mit den Einheitsvektoren auf den Koordinatenachsen:
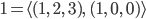
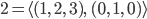
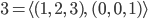
Ben Und welches Skalarprodukt nimmst du, liebe Rike?
Rike Na, im reellen endlich dimensionalen Vektorraum über 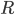 nehme ich:
nehme ich:
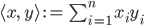
und über 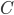 :
:
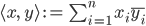
Im 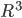 wäre das
wäre das
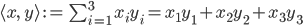
Ben Okay, ist ja okay.
Die Wiezorek-Projektionsaufgabe
Rike Jetzt kann ich so eine typische Wiezorek-Projektionsaufgabe: Berechne die orthogonale Projektion 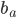 des Vektors
des Vektors
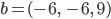
auf den Vektor
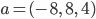
sehr viel klarer und schneller lösen!
Ben Aha!
Rike Ja, Wir machen aus 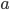 einen Einheitsvektor
einen Einheitsvektor  , in dem wir durch seine Länge teilen und projizieren
, in dem wir durch seine Länge teilen und projizieren 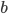 auf
auf  :
:
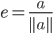
Damit kriegen wir sofort die Lösung:
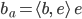
Ben Na gut, das ist schon überzeugend, es steckt aber viel Mathematik in diesem Zerlegungssatz drin!
Rike Stimmt, doch am Ende ist er sehr folgerichtig und intuitiv! Oder war er etwa zu abstrakt für dich?
Ben Hahaha!
***
Übungsaufgaben
- Löse die Wiezorek-Projektionsaufgabe!
- Vergleiche den Aufwand und Abstraktionsgrad mit dem von Wiezorek aus der Formel
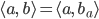
und dem Ansatz
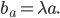
Lösungen
Rikes Zugang
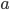 wird normiert:
wird normiert:
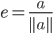
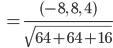
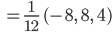
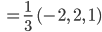
Projektion von 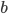 auf diesen Einheitsvektor:
auf diesen Einheitsvektor:
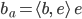
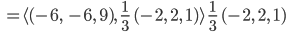
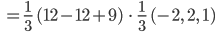
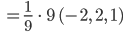
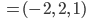
Wiezoreks Lösungsweg
Aus Betrachtungen zur Arbeit ergibt sich
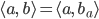
Mit dem Ansatz, dass 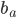 auf der Geraden
auf der Geraden 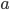 liegt – in parametrischer Schreibweise
liegt – in parametrischer Schreibweise
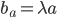
erhält er:
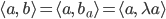
Nun berechnet er das Skalarprodukt von 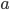 und
und 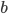 :
:
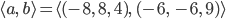
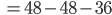
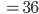
Jetzt kommt die andere Seite der oberen Gleichung. Es ist
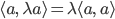
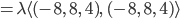
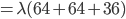
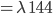
Wegen
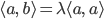
erhält er nun:
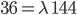
also
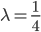
und so mit dem Ansatz
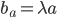
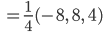
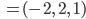
Ziemlich umständlich!
