Wie Schüler:Innen und Lehrer:Innen an parallelen Geraden und Koordinatensystemen verzweifeln

Ben und Rike sitzen zusammen, Rike erzählt eine Geschichte aus ihrem Matheunterricht damals in der Schule.

Die Verzweiflung von Rikes Lehrer

Rike Als ich in die weiterführende Schule kam, hatten wir endlich Geometrie: Punkte, Geraden, Kreise, wir haben Winkel gemessen, Dreiecke gezeichnet usw. Ich erinnere mich noch, als unser Mathelehrer, Herr Wiezorek, uns parallele Geraden erklärte: Dazu muss man an eine gegebene Gerade ein Zeichendreieck anlegen und daran wieder ein Lineal, schaut mal, so:

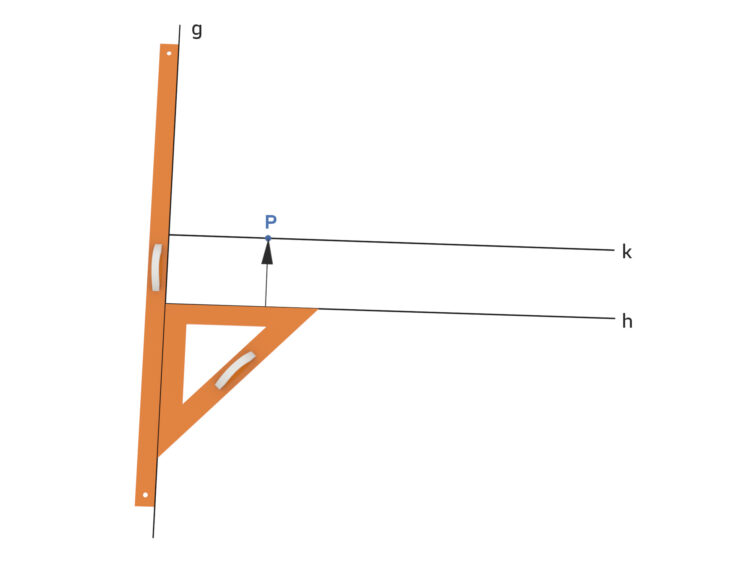
Das Tafeldreieck sollten wir entlang des Lineals nach oben oder nach unten verschieben. So konnten wir eine neue Gerade durch einen Punkt P zeichnen. Das war dann die parallele Gerade. Das Tafeldreieck, was Herr Wiezorek hatte, hatte einen Griff, der mit fetten 2 Schrauben von der Rückseite her angebracht war. Folglich konnte er sein Dreieck nicht richtig an das Lineal angelegen.  Folglich konnte er das Tafeldreieck auch nicht richtig verschieben. Das Tafellineal hatte auch einen blöden Griff, haha, und mit dem konnte Keiner einen richtig geraden oder parallelen Kreidestrich ziehen! Das Bild sah total vermurkst aus. Wiezorek seufzte und entschuldigte sich:

Das falsch verstandene Parallelenaxiom

Also 2 Geraden sind parallel, wenn sie sich niemals schneiden oder höchstens im Unendlichen, sagte Wiezorek, seht mal, wenn das jetzt 2 Fahrbahnen einer Autobahn wären, dann würden die sich nie schneiden.

Seht ihr, wenn ich die so perspektivisch zeichne, dann könnte man sagen, die beiden Fahrbahnen – also die parallelen Geraden – schneiden sich im Unendlichen, sagte Wiezorek, das versteht ihr doch, Kinder? Nein, das haben wir nicht verstanden. Es meldete sich auch gleich jemand und fragte, ob die Autos im Unendlichen zusammenstoßen? Ob das wohl die Hölle ist, dieses Unendliche? Es gab eine Riesendiskussion über das Unendliche mit uns Sechstklässlern.

Später habe ich herausgefunden, dass dieses Schneiden im Unendlichen das Parallelenaxiom von Euklid ist – was Wiezorek auch noch falsch verstanden hat, denn die Geraden h und k dürfen sich, wenn man sie bis ins Unendliche verlängert, niemals schneiden.

Ben Sag mal Rike, du weißt ja ziemlich gut über parallele Geraden Bescheid! Hast du mich nicht damals im Lokschuppen nach dem Parallelenaxiom gefragt?

Rike Ja, habe ich das?

Ben Hey! Das war ein Trick! Und weiter?

Das kartesische Koordinatensystem

Rike Wir haben dann 2- und 3-dimensionale Koordinatensysteme mit rechtwinkligen Achsen gezeichnet. Außerdem sollten wir an jede Achse die Länge von 1 cm markieren. Die x-Achse sollten wir im Winkel von 45° zur y-Achse zeichnen und die 1 bei 0,7 cm abtragen.

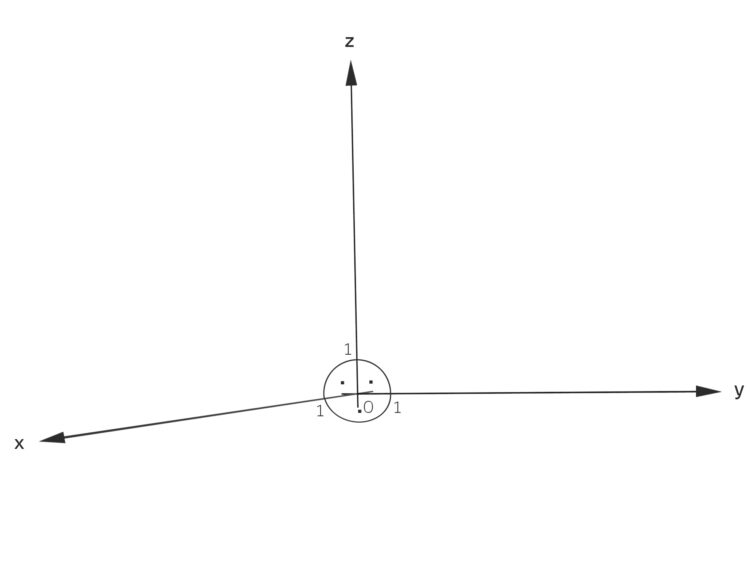
Ben Ist ja okay. An die 45° hast du dich wieder nicht gehalten?!

Rike Naja, im Buch stand, dass es auch noch andere Möglichkeiten des Schrägbildes gibt. Und, höre, mein Freund Fred – mein Sitznachbar und Linkshändler – hat die Achsen anders gezeichnet. Irgendein Punkt P, nehmen wir mal

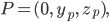
im kartesischen Koordinatensystem sieht bei ihm spiegelverkehrt zu meinem aus.

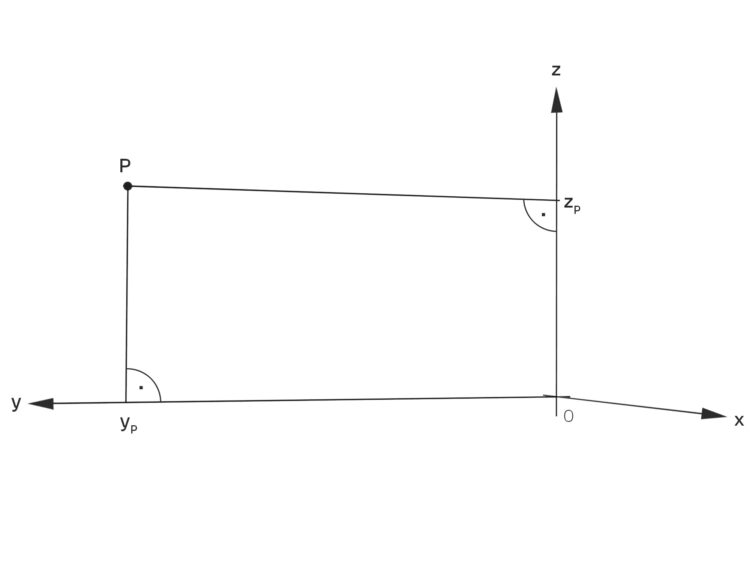
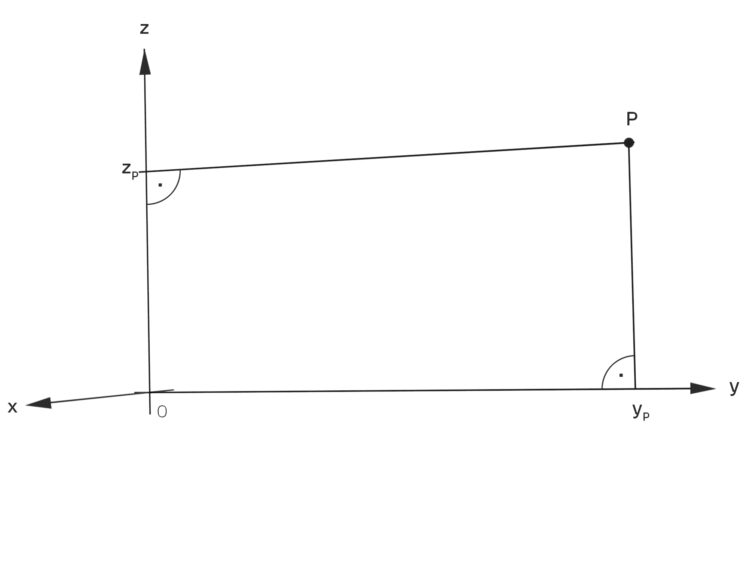
Wiezorek hat sich ziemlich aufgeregt und wusste nicht, dass er für ein kartesisches Koordinatensystem ein rechtshändiges oder eine Orientierung verlangen muss…

Ben Naja, das erklärt sich wirklich umständlich, vor allem Linkshändlern gegenüber.

Rikes alternative Lösung

Rike Ach, weißt du, er könnte ja einfach fordern: Ein korrektes rechtshändiges Koordinatensystem ist so eins, das man mit einer speziellen Drehung aus dem Standardsystem erhält.

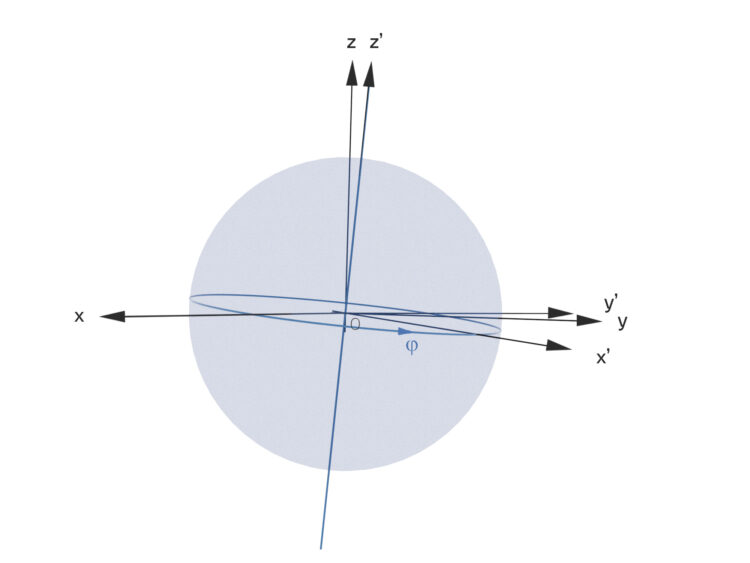
Ben Hahaha! Gruppentheorie im Gymnasium!

***

Übungsaufgaben

1. Welche Eigenschaften müssen solche speziellen Drehungen haben?
2. Was ist mit Freds Koordinatensystem?

Lösungen

1. Die Drehungen sollten weder die Längen der Vektoren noch deren relative Lage im Raum ändern, d.h. ihre Orientierung. Da man alle Drehungen im 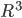durch Matrizen ausdrücken kann, kommt man darauf, dass die Determinante der Matrix 1 sein muss. Diese Matrizen haben eine große Bedeutung in vielen Anwendungen und bilden eine Gruppe, sie heißen Spezielle Lineare Gruppe: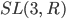
2. Freds Koordinatensystem kann aus Wiezoreks Koordinatensystem nur durch eine Spiegelung erhalten werden, eine Matrixanwendung mit negativer Determinante. Dabei ändert sich die Orientierung der beteiligten Vektoren.